GEEM - Situation d’apprentissage

B2. Sens des opérations

Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne.

Situation d’apprentissage 1 : cible mathématique

Durée totale : environ 2 heures 20 minutes

Sommaire

Dans cette situation d’apprentissage, les élèves manipulent les nombres naturels en créant un jeu de fléchettes. La propriété de distributivité de la multiplication facilitera la conception du jeu et le calcul mental nécessaire à son déroulement.

Attente	Contenus d'apprentissage
B2. Sens des opérations Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne.	B2.1 Utiliser les propriétés des opérations et les relations entre les opérations pour résoudre des problèmes comportant des nombres naturels, des nombres décimaux, des fractions, des rapports, des taux, et des pourcentages, y compris des problèmes à plusieurs étapes ou plusieurs opérations. B2.6 Représenter des nombres composés sous la forme d’une multiplication de ses facteurs premiers, y compris à l’aide de l’arbre de facteurs.

Attente

Contenus d'apprentissage

B2. Sens des opérations

Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne.

B2.1 Utiliser les propriétés des opérations et les relations entre les opérations pour résoudre des problèmes comportant des nombres naturels, des nombres décimaux, des fractions, des rapports, des taux, et des pourcentages, y compris des problèmes à plusieurs étapes ou plusieurs opérations.

B2.6 Représenter des nombres composés sous la forme d’une multiplication de ses facteurs premiers, y compris à l’aide de l’arbre de facteurs.

Intention pédagogique

Cette situation d’apprentissage a pour but d’amener les élèves à :

appliquer la propriété de distributivité de la multiplication sur l’addition;
développer des stratégies de calcul mental;
développer des stratégies de résolution de problèmes.

Contexte pédagogique	Préalables
Au cycle primaire, les élèves apprennent à décomposer des nombres naturels et explorent certaines des propriétés des opérations, notamment, la commutativité de l’addition et de la multiplication. En 4^e année, elles et ils voient la propriété d’associativité de l’addition et de la multiplication, et la propriété de distributivité de la multiplication sur l’addition. En 5^e année, elles et ils utilisent la propriété de distributivité pour estimer et vérifier le produit de deux nombres. En 6^e année, la propriété de distributivité est utilisée comme stratégie de calcul mental.	La présente situation d’apprentissage permet aux élèves de recourir à leurs connaissances des opérations pour résoudre mentalement des équations. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent : connaître diverses stratégies d’addition, de soustraction et de multiplication; comprendre le concept de multiplication ainsi que la propriété de distributivité; comprendre qu’un nombre peut être décomposé de différentes façons.

Contexte pédagogique

Préalables

Au cycle primaire, les élèves apprennent à décomposer des nombres naturels et explorent certaines des propriétés des opérations, notamment, la commutativité de l’addition et de la multiplication. En 4^e année, elles et ils voient la propriété d’associativité de l’addition et de la multiplication, et la propriété de distributivité de la multiplication sur l’addition. En 5^e année, elles et ils utilisent la propriété de distributivité pour estimer et vérifier le produit de deux nombres.

En 6^e année, la propriété de distributivité est utilisée comme stratégie de calcul mental.

La présente situation d’apprentissage permet aux élèves de recourir à leurs connaissances des opérations pour résoudre mentalement des équations.

Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :

connaître diverses stratégies d’addition, de soustraction et de multiplication;
comprendre le concept de multiplication ainsi que la propriété de distributivité;
comprendre qu’un nombre peut être décomposé de différentes façons.

Vocabulaire mathématique

commutativité, distributivité, décomposer

Matériel

annexe 6.8 (Distributivité de la multiplication)
annexe 6.1 (Description du jeu de fléchettes)
annexe 6.2 (Cible du jeu)
annexe 6.5 (Création d’une cible)
annexe 6.3 (Jeu de fléchettes (version 1)) (1 copie par élève)
annexe 6.4 (Jeu de fléchettes (version 2)) (1 copie par élève)
annexe 6.6 (Cible) (1 copie par équipe)
annexe 6.7 (Fléchettes) (1 copie par équipe)

Activité préparatoire facultative

Durée : environ 30 minutes

Si nécessaire, revoir la propriété de distributivité de la multiplication à l’aide de l’annexe 6.8. Les séries d’opérations apparentées présentées misent sur l’application de cette propriété.

Avant l’apprentissage (mise en train)

Durée : environ 1 heure

Dans la mise en train, les élèves apprennent à jouer à un jeu de fléchettes modifié.

Le jeu en question est expliqué à l’annexe 6.1.

Au début, l’accent est mis sur la relation d’égalité entre les points générés par une fléchette et la somme des points obtenus par deux autres fléchettes. Par la suite, en jouant, en analysant le jeu et en discutant, l’importance de la propriété de distributivité comme stratégie de jeu sera mise en évidence.

Présenter la situation suivante.

Dans le cadre d’une campagne de financement, une école organise une foire mathématique. Chaque classe doit concevoir un jeu qui fait appel à des connaissances ou à des habiletés mathématiques. Les élèves d’une classe de 6^e année ont préparé un jeu de fléchettes et elles et ils aimeraient que les élèves d’une autre classe de 6^e année l’essaient avant la foire.

Présenter l’annexe 6.2 au tableau interactif ou la reproduire au tableau et la décrire (voir annexe 6.1). Préciser aux élèves que ce jeu est différent du jeu de fléchettes traditionnel.

Expliquer les deux versions du jeu à l’aide des deux exemples ci-après pour éviter de présenter les situations que les élèves auront à résoudre en annexes 6.3 et 6.4.

Version 1

Placer une fléchette dans le secteur 6 de l’anneau (\( \times \;5\)) et une deuxième dans le secteur 4 de l’anneau (\( \times \;5\)).

Demander aux élèves de :

suggérer une façon de représenter les calculs à effectuer afin de déterminer la somme des points obtenus par les deux fléchettes;
déterminer l’emplacement possible d’une troisième fléchette pour que le nombre de points générés par cette fléchette soit égal à la somme des points obtenus par les deux autres fléchettes.

Écrire les phrases mathématiques qui correspondent aux divers calculs.

Exemple

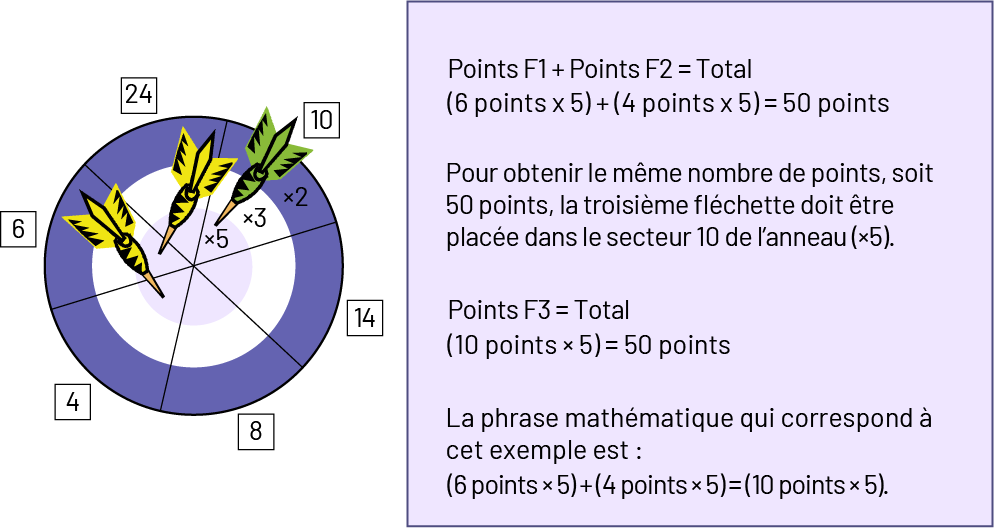
Version 2

Placer une fléchette dans le secteur 4 de l’anneau (\( \times \;5\)).

Demander aux élèves de :

suggérer une façon de représenter le calcul à effectuer afin de déterminer le total des points générés par cette fléchette;
déterminer l’emplacement possible de deux autres fléchettes pour que la somme des points obtenus par ces deux fléchettes soit égale aux points générés par la première fléchette.

Écrire les phrases mathématiques qui correspondent aux divers calculs.

Exemple

S’assurer que les élèves comprennent bien le jeu. Grouper les élèves par deux et distribuer une copie des annexes 6.3 et 6.4 à chaque équipe.

Discuter avec eux du travail à effectuer. S’assurer qu’elles et ils comprennent bien ce qui est demandé. Allouer suffisamment de temps pour leur permettre d’effectuer les tâches.

Note : Ces tâches permettent de vérifier la compréhension des élèves du jeu et de faire ressortir l’utilité de la propriété de distributivité de la multiplication sur l’addition. Il est possible, particulièrement à la situation 4, que certains élèves déterminent une combinaison qui ne fait pas appel à cette propriété, par exemple : \(24\;\;{\rm{points}}\; \times \;5\; = \;\left( {15\;\;{\rm{points}}\; \times \;5} \right)\; + \;\left( {15\;\;{\rm{points}}\; \times \;3} \right)\; = \;120\;\;{\rm{points}}\).

Cette combinaison est toutefois valable puisque le respect de la propriété de distributivité ne fait pas partie des règles du jeu.

Circuler, observer et, si nécessaire, intervenir pour aider les élèves à compléter la section B de l’annexe 6.3. Attirer leur attention sur l’emplacement des deux fléchettes; elles correspondent à deux façons de décomposer 14 par l’addition, soit 10 et 4, et 6 et 8.

Demander, au besoin, aux élèves de représenter les opérations à l’aide de dispositions rectangulaires.

Exemple

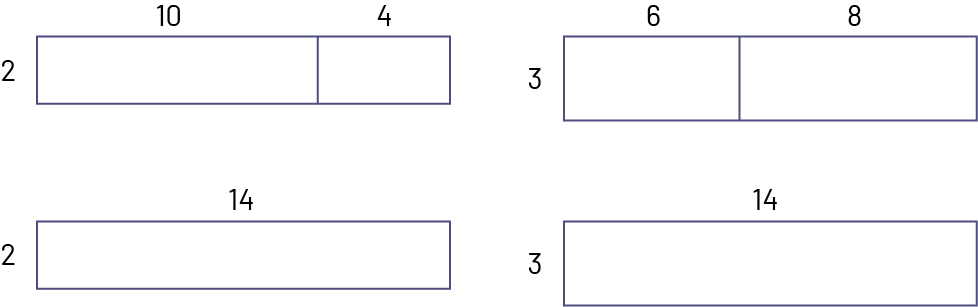
Pour la situation 4 de l’annexe 6.4, les élèves doivent ajouter les points manquants dans trois des secteurs de la cible; pour ce faire, ils doivent tenir compte du nombre de points générés par la fléchette placée dans le secteur 24 de l’anneau (\( \times \;5\)).

En groupe classe, revenir sur les situations. Écrire au tableau différentes combinaisons et leurs phrases mathématiques correspondantes afin de faire ressortir l’utilité de la décomposition ou de la composition d’un nombre et de la propriété de distributivité de la multiplication sur l’addition.

Exemple pour la situation 2

Combinaison : \({\rm{Points}}\;\;\;{\rm{F1}}\;{\rm{ + }}\;\;{\rm{Points}}\;\;\;{\rm{F2}}\; = \;{\rm{Points}}\;\;\;{\rm{F3}}\)

Phrase mathématique : \(\left( {8\;\;{\rm{points}}\; \times \;{\rm{3}}} \right)\; + \;\left( {6\;\;{\rm{points}}\; \times \;{\rm{3}}} \right)\; = \;14\;\;{\rm{points}}\; \times \;{\rm{3}}\)

Composition d’un nombre :

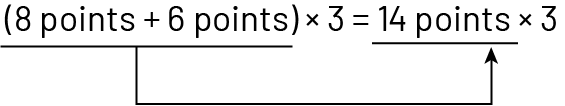
Distributivité de la multiplication sir l’addition :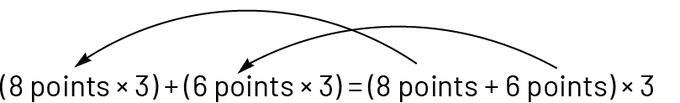

Utilité : la composition du nombre 14 (\(8\; + \;6\)) permet de trouver le secteur dans lequel placer la troisième fléchette. La distributivité permet d’effectuer le calcul plus facilement.

Faire remarquer que la propriété de distributivité de la multiplication sur l’addition peut aussi s’effectuer sur le deuxième facteur du produit au lieu du premier.

Par exemple, dans la situation 3, il est possible de décomposer le deuxième facteur comme suit :

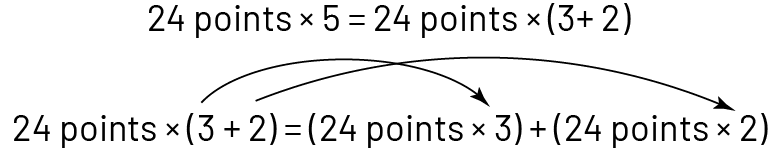
Cette caractéristique de la propriété de distributivité permet d’obtenir plus de possibilités de combinaisons de fléchettes.

Écrire au tableau quelques nombres choisis par les élèves comme points manquants dans trois secteurs de la situation 4.

À partir des phrases mathématiques formulées, faire ressortir la propriété de distributivité de la multiplication sur l’addition.

Exemple

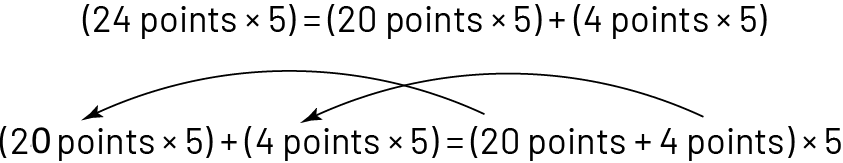
Afin de consolider le concept de distributivité, présenter une combinaison acceptable pour la situation 4, qui permet d’établir une relation d’égalité entre les points générés par une fléchette et la somme des points obtenus par deux autres fléchettes, mais qui ne respecte pas la propriété de distributivité de la multiplication sur l’addition. Les élèves doivent saisir le sens de la distributivité puisque dans le jeu qu’ils créeront ultérieurement, le respect de cette propriété fera partie des règles du jeu.

Exemple

Pendant l’apprentissage (exploration) - équipes de 2

Durée : environ 1 heure

Présenter la situation suivante :

La cible du jeu de fléchettes avec laquelle nous avons joué précédemment contient 6 secteurs. Maintenant, vous devez créer une cible qui contient 8 secteurs. De plus, une seconde règle s’ajoute à la première : une combinaison ne sera acceptée que si elle respecte la propriété de distributivité de la multiplication sur l’addition.

Présenter l’annexe 6.5 au tableau interactif et expliquer aux élèves la tâche à effectuer.

Grouper les élèves par deux.

Distribuer à chaque équipe une copie des annexes 6.6 et 6.7.

Leur suggérer de découper et d’utiliser les fléchettes pour visualiser plus facilement les combinaisons possibles.

Dire aux élèves de discuter et de créer leur cible en utilisant une variété de stratégies. Par exemple, afin de déterminer les nombres à inscrire dans leur cible, les élèves peuvent :

procéder par essais et erreurs;
effectuer divers calculs afin d’établir des relations d’égalité entre les points générés par une fléchette et la somme des points obtenus par deux autres fléchettes;
décomposer des nombres afin de s’assurer que la distributivité est respectée.

Allouer suffisamment de temps pour permettre aux élèves de créer leur cible. Circuler et intervenir au besoin. Porter une attention particulière aux stratégies qu’utilisent les élèves pour déterminer les nombres et les combinaisons possibles.

Observations possibles	Interventions possibles
Les élèves ne savent pas quels nombres choisir pour compléter la cible.	Leur poser les questions suivantes : Quels nombres figuraient dans la cible du premier jeu? Qu’avaient-ils en commun? De quelle façon pouvez-vous décomposer un des nombres inscrits sur la cible?
Certains élèves forment des combinaisons qui ne respectent pas la propriété de distributivité. Par exemple : \(\left( {28\; \times \;1} \right)\; = \;\left( {8\; \times \;1} \right)\, + \;\left( {5\; \times \;4} \right)\).	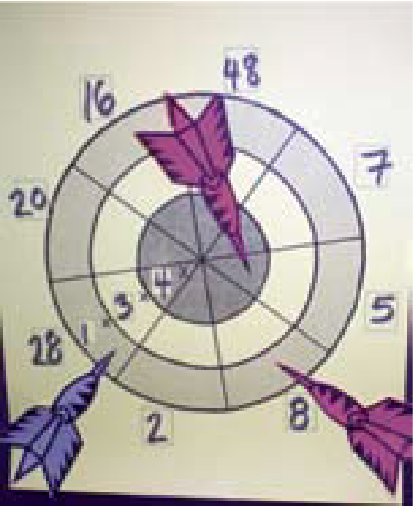Leur poser les questions suivantes : Quelles règles votre jeu doit-il respecter? (La relation d’égalité entre les points générés par une fléchette et la somme des points obtenus par deux autres fléchettes, et la distributivité de la multiplication sur l’addition.) Est-ce que toutes vos combinaisons respectent la propriété de distributivité? Est-ce qu’un des deux nombres a été décomposé à l’aide de l’addition? Dans les exemples au tableau, où se retrouvent la décomposition et la distributivité?
Lors du choix des effets multiplicateurs, quelques équipes confondent la décomposition d’un nombre sous forme de somme avec celle d’un nombre sous forme de produit. Par exemple, ils choisissent les nombres 2, 5 et 10 comme effets multiplicateurs et affirment que la combinaison des trois fléchettes ci-dessus est acceptable, soit : \(10\; \times \;10\; = \;\left( {10\; \times \;2} \right)\; + \;\left( {10\; \times \;5} \right)\).	Leur demander par exemple : Pourriez-vous vérifier si \(\left( {10\; \times \;10} \right)\; = \;\left( {10\; \times \;2} \right)\; + \;\left( {10\; \times \;5} \right)\)? Pourquoi la phrase mathématique est-elle fausse? Leur dire de dessiner une disposition rectangulaire qui illustre cette phrase mathématique et leur poser la question suivante : Quels nombres peuvent remplacer le 2 et le 5 pour rendre cette phrase mathématique vraie? 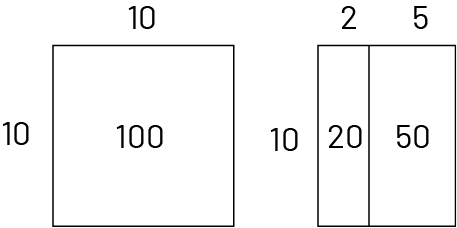Note : Pour respecter la propriété de distributivité de la multiplication sur l’addition, le nombre 10 doit être décomposé à l’aide d’une somme (par exemple, \(1\; + \;9\); \(2\; + \;8\); \(3\; + \;7\); \(4\; + \;6\)) et non d’un produit (par exemple, \(2\; \times \;5\)).
Les élèves ont complété leur cible, mais ils ne parviennent pas à écrire les combinaisons.	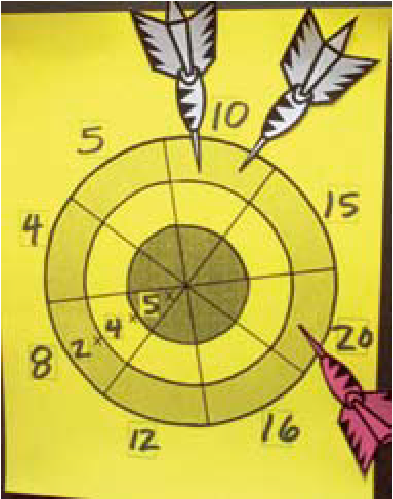Leur poser la question suivante : Lorsque vous avez choisi vos nombres, à quelles combinaisons pensiez-vous? Leur dire ensuite de placer les fléchettes sur les nombres choisis et d’inscrire, au fur et à mesure, toutes les combinaisons possibles, en suivant la structure des phrases mathématiques de l’activité précédente.

Lorsque les équipes ont terminé la tâche, leur demander de noter, sur une grande feuille, les combinaisons découlant des nombres qu’ils ont choisis. Spécifier aux élèves que les nombres doivent être lisibles à distance et que le contenu de cette grande feuille doit être clair et précis afin que les autres élèves comprennent bien leur raisonnement pendant l’échange mathématique.

Après l’apprentissage (objectivation/transfert de connaissances)

Durée : environ 20 minutes

Demander à quelques équipes de présenter leur cible et d’expliquer leur démarche en formulant des arguments clairs, basés sur des termes de causalité ou de conséquence logique, tels que :

Lorsque j’ai choisi les nombres \(x\) et \(y\), je savais que je devais placer les fléchettes dans l’anneau (\( \times \;2\)) parce que la première fléchette est placée dans cet anneau.
J’ai d’abord inscrit 12 et 8 autour de notre cible. J’ai ensuite déterminé que le troisième nombre serait 20 puisque \(12\; + \;8\; = \;20\).
Puisque la somme de deux des effets multiplicateurs que nous avons choisis (1 et 2) correspond au troisième effet multiplicateur (3), nous obtenons automatiquement 8 combinaisons possibles, et ce, peu importe les nombres choisis pour les secteurs.

Inviter les autres élèves à réagir à chacune des présentations en faisant part de leurs observations ou en posant des questions. Faciliter le déroulement de l’échange mathématique en posant au besoin des questions telles que :

Est-ce que quelqu’un peut expliquer pourquoi la somme des points obtenus par les deux fléchettes données est égale au nombre de points générés par la troisième fléchette?
Lorsque vous cherchiez des combinaisons possibles, y en a-t-il qui étaient plus faciles à trouver? Lesquelles? Pourquoi ? [Il est possible que les élèves mentionnent que les combinaisons reliées à la décomposition selon la valeur de position (par exemple, \(12\; = \;10\; + \;2\)) ou celles reliées aux doubles (par exemple, \(12\; = \;6\; + \;6\)) étaient plus évidentes pour eux.]
Quels nombres, parmi ceux qui figurent autour de la cible, ont été placés en premier? Comment avez-vous ensuite choisi les autres?
Avez-vous dû changer un ou des nombres qui ne donnaient aucune combinaison? Si oui, lequel ou lesquels? Qu’est-ce qui vous a permis de remarquer que ce ou ces nombres n’étaient pas utiles?
Y a-t-il des combinaisons qui ont été oubliées? Si oui, lesquelles?
Quelle version du jeu (une ou deux fléchettes) vous a permis de trouver plus facilement vos combinaisons?
Combien de combinaisons gagnantes avez-vous trouvées?

Cet échange mathématique a pour but de faire remarquer aux élèves que la propriété de distributivité de la multiplication est une méthode de calcul mental très efficace.

Suggérer ensuite aux élèves d’expliquer comment cette stratégie peut les aider à manipuler des faits numériques plus difficiles (par exemple, \(15\; \times \;4\; = \;\left( {15\; \times \;2} \right)\; + \;\left( {15\; \times \;2} \right)\; = \;60\)) ou à effectuer la multiplication d’un nombre à trois chiffres par un nombre à deux chiffres (par exemple, \(172\; \times \;12\; = \;\left( {172\; \times \;10} \right)\; + \;\left( {172\; \times \;2} \right)\) ou \(\left( {100\; \times \;12} \right)\; + \;\left( {70\; \times \;12} \right)\; + \;\left( {2\; \times \;12} \right)\).

Si nécessaire, démontrer le lien entre la distributivité de la multiplication et l’algorithme usuel de la multiplication.

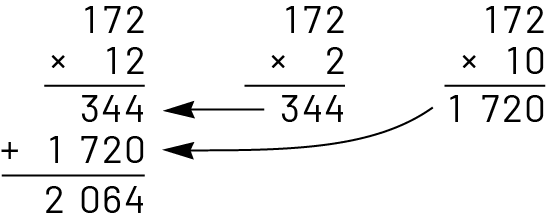
Note : Au moment qui vous semblera opportun, permettre aux équipes d’échanger leur jeu de fléchettes. Ainsi, en jouant, les élèves appliquent et approfondissent la propriété de distributivité comme stratégie de calcul mental.

Différenciation pédagogique

L’activité peut être modifiée pour répondre aux différents besoins des élèves.

Pour faciliter la tâche	Pour enrichir la tâche
Fournir aux élèves quelques nombres repères qui leur permettront d’identifier une première combinaison; Leur permettre de compléter la cible avec 6 nombres au lieu de 8; Leur suggérer 3 nombres pour les effets multiplicateurs afin qu’ils se concentrent sur la décomposition d’un seul des termes de la multiplication.	Suggérer aux élèves de trouver des nombres permettant au moins 15 combinaisons; Leur demander de créer une cible en fonction du nombre de secteurs et d’anneaux de leur choix; Leur suggérer de créer une cible dont la règle du jeu est de déterminer une relation d’égalité entre les points générés par une fléchette et la différence entre les points obtenus par deux autres fléchettes. (Le jeu est alors axé sur la propriété de distributivité de la multiplication sur la soustraction.) Exemples

Pour faciliter la tâche

Pour enrichir la tâche

Fournir aux élèves quelques nombres repères qui leur permettront d’identifier une première combinaison;
Leur permettre de compléter la cible avec 6 nombres au lieu de 8;
Leur suggérer 3 nombres pour les effets multiplicateurs afin qu’ils se concentrent sur la décomposition d’un seul des termes de la multiplication.

Suggérer aux élèves de trouver des nombres permettant au moins 15 combinaisons;
Leur demander de créer une cible en fonction du nombre de secteurs et d’anneaux de leur choix;
Leur suggérer de créer une cible dont la règle du jeu est de déterminer une relation d’égalité entre les points générés par une fléchette et la différence entre les points obtenus par deux autres fléchettes. (Le jeu est alors axé sur la propriété de distributivité de la multiplication sur la soustraction.)

Exemples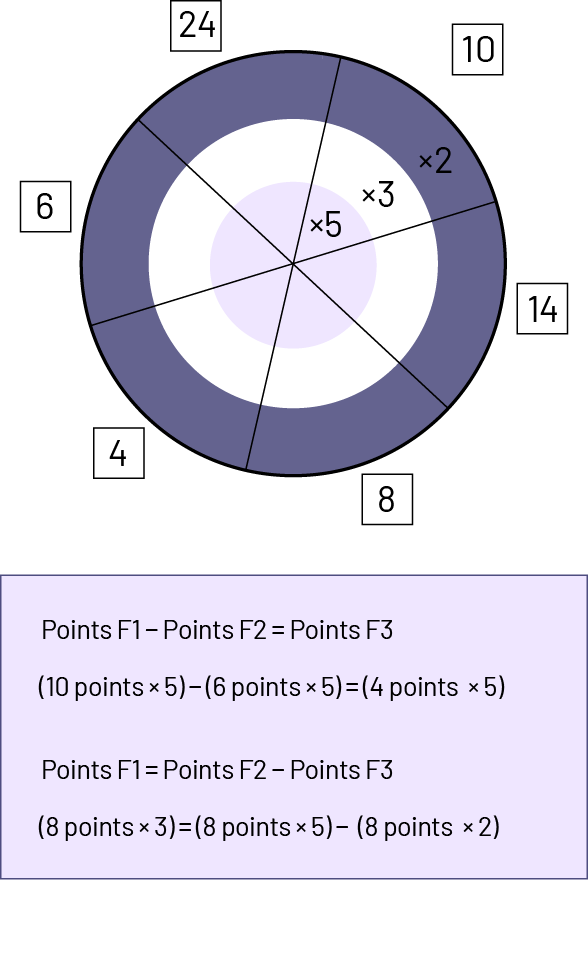

Suivi à la maison

Demander aux élèves d’apporter à la maison la cible conçue pour jouer au jeu de fléchettes. Leur préciser la marche à suivre, soit :

Expliquer les règles du jeu à un membre de leur famille.

Placer une ou deux fléchettes sur la cible selon la version choisie.

Demander à la personne de placer la ou les fléchettes correspondantes selon les règles du jeu.

Vérifier la solution.

Expliquer l’utilisation de la propriété de distributivité.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 195-207.