B2. Operations
Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life.
Learning Situation 1: Mathematical Target
Duration: approximately 2 hours 20 minutes
Overview
In this learning situation, students manipulate whole numbers by creating a dart game. The distributive property of multiplication will facilitate the design of the game and the mental math required to play it.
| Overall Expectation | Specific Expectations |
|---|---|
|
B2. Operations Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life. |
B2.1 Use the properties of operations, and the relationships between operations, to solve problems involving whole numbers, decimal numbers, fractions, ratios, rates, and whole number percents, including those requiring multiple steps or multiple operations. B2.6 Represent composite numbers as a product of their prime factors, including through the use of factor trees. |
Learning Goals
The purpose of this learning situation is to have students:
- apply the distributive property of multiplication to addition;
- develop mental calculation strategies;
- develop problem-solving strategies.
| Learning Context | Prerequisites |
|---|---|
|
In the primary grades, students learned to decompose numbers and explored some of the properties of operations, notably the commutative property of addition and multiplication. In Grade 4, they were introduced to the associative property of addition and multiplication, and the distributive property of multiplication over addition. In Grade 5, they used the distributive property to estimate and verify the product of two numbers. In Grade 6, the distributive property is used as a mental strategy. |
This learning situation allows students to use their knowledge of operations to mentally solve equations. To complete this learning task, students must be able to:
|
Mathematical Vocabulary
commutative property, distributive property, decomposition
Materials
- Appendix 6.1 (Description of the darts game)
- Appendix 6.2 (Target of the game)
- Appendix 6.5 (Creation of a target)
- Appendix 6.3 (Dart game (version 1)) (1 copy per student)
- Appendix 6.4 (Dart game (version 2)) (1 copy per student)
- Appendix 6.6 (Target) (1 copy per team)
- Appendix 6.7 (Darts) (1 copy per team)
Before Learning (Warm-Up)
Duration: approximately 1 hour
In the warm-up, students learn to play a modified dart game.
The game is explained in Appendix 6.1.
Initially, the focus is on the equal relationship between the points generated by one dart and the sum of the points obtained by two other darts. Later, through play, analysis of the game, and discussion, the importance of the distributive property as a game strategy will be highlighted.
Present the following problem situation:
As part of a fundraising campaign, a school organizes a math fair. Each class is asked to design a game that uses math knowledge or skills. Students in one Grade 6 class have developed a dart game and would like students in another Grade 6 class to try it out before the fair.
Present Appendix 6.2 on the interactive whiteboard or reproduce it on the board and describe it (see Appendix 6.1). Explain to students that this game is different from traditional darts.
Explain the two versions of the game using the two examples below to avoid presenting the situations that students will have to solve in Appendices 6.3 and 6.4.
Version 1
Place a dart in sector 6 of the ring (\( \times \;5\)) and a second one in sector 4 of the ring (\( \times \;5\)).
Ask students to:
- suggest a way to represent the calculations to determine the sum of the points obtained by the two darts;
- determine the possible location of a third dart so that the number of points generated by it is equal to the sum of the points obtained by the other two darts.
Write the number sentences that correspond to the various calculations.
Example

Version 2
Place a dart in sector 4 of the ring (\( \times \;5\)).
Ask students to:
- suggest a way to represent the calculation to determine the total points generated by this dart;
- determine the possible location of two more darts so that the sum of the points obtained by these two darts is equal to the points generated by the first dart.
Write the number sentences that correspond to the various calculations.
Example

Group students in pairs and distribute a copy of Appendices 6.3 and 6.4 to each team.
Discuss with them the work to be done. Make sure they understand what is required. Allow sufficient time for them to complete the tasks.
Note: These tasks test students' understanding of the game and highlight the usefulness of the distributive property of multiplication over addition. It is possible, especially in Situation 4, that some students will determine a combination that does not use this property, for example: \(24\;{\rm{dots}}\; \times \;5\; = \;\left( {15\;{\rm{dots}}\; \times \;5} \right)\; + \;\left( {15\;{\rm{dots}}\; \times \;3} \right)\; = \;120\;{\rm{dots}}\).
However, this combination is valid since the respect of the distributive property is not part of the rules of the game.

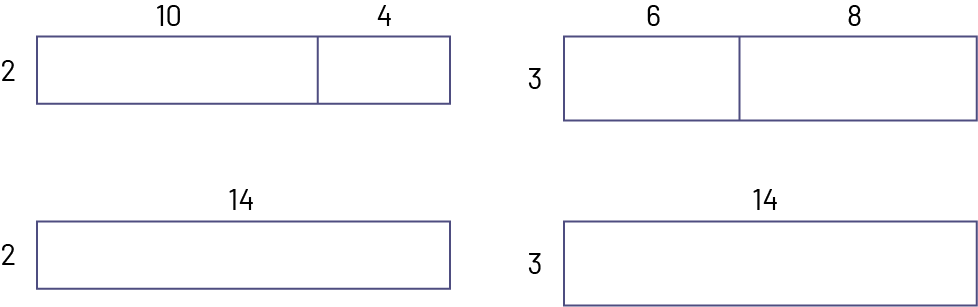
Circulate, observe and, if necessary, provide support to students as they complete Section B of Appendix 6.3. Draw their attention to the location of the two darts; they correspond to two ways of decomposing 14 by addition, 10 and 4, and 6 and 8.
If necessary, have students represent the operations using rectangular linear models.
Example
For Situation 4 in Appendix 6.4, students must add the missing points in three of the target areas by taking into account the number of points generated by the dart placed in area 24 of the ring \(\times \;5\).
As a class, review the situations. Write different combinations and their corresponding number sentences on the board in order to highlight the usefulness of decomposing or composing a number and of the distributive property of multiplication over addition.
Example for Situation 2
Combination: \({\rm{Points}}\;{\rm{F1}}\;{\rm{ + }}\;{\rm{Points}}\;{\rm{F2}}\; = \;{\rm{Points}}\;{\rm{F3}}\)
Number sentence: \(\left( {8\;{\rm{points}}\; \times \;{\rm{3}}} \right)\; + \;\left( {6\;{\rm{points}}\; \times \;{\rm{3}}} \right)\; = \;14\;{\rm{points}}\; \times \;{\rm{3}}\)
Composition of a number:
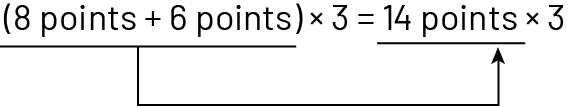
Distributive property of multiplication with addition: 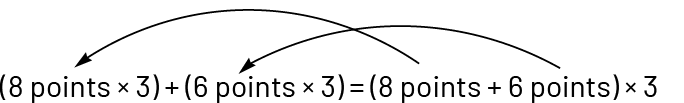
Usefulness: dialing the number 14 (\(8\; + \;6\)) helps find the area in which to place the third dart. The distributivite property makes the calculation easier.
Point out that the distributive property of multiplication over addition can also be performed on the second factor of the product instead of the first.
For example, in Situation 3, the second factor can be decomposed as follows:
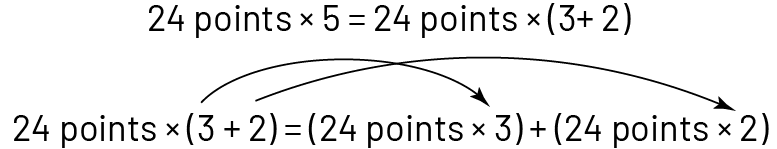
This feature of the distributive property allows for more possibilities of dart combinations.
Write on the board some numbers chosen by the students as missing points in three sectors of Situation 4.
From the number sentences formulated, bring out the distributive property of multiplication over addition.
Example
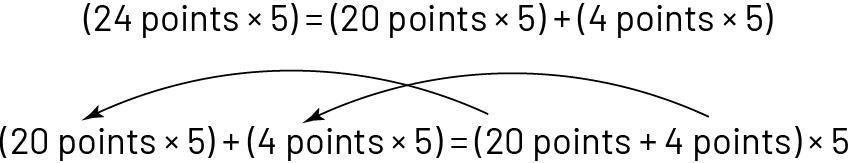
In order to consolidate understanding of the distributive property, present an acceptable combination for Situation 4, which establishes an equality relationship between the points generated by one dart and the sum of the points obtained by two other darts, but which does not respect the distributive property of multiplication over addition.
In the game that the students will create later, respect for this property will be part of the rules of the game.
Example

Active Learning (Exploration)
Duration: approximately 1 hour
Present the following situation:
The dartboard we played with earlier contains 6 sectors. Now you have to create a target that contains 8 sectors. In addition, there is a second rule: a combination will only be accepted if it respects the distributive property of multiplication over addition.
Present Appendix 6.5 on the interactive whiteboard and explain the task to the students.
Group students in pairs.
Distribute a copy of Appendices 6.6 and 6.7 to each team.
Suggest that they cut out and use the darts to more easily visualize the possible combinations.

Tell students to discuss and create their target using a variety of strategies. For example, in order to determine the numbers to put in their target, students can:
- proceed by trial and error;
- perform various calculations to establish relationships of equality between the points generated by one dart and the sum of the points obtained by two other darts;
- decompose numbers to ensure that the distributive property is respected.
Allow sufficient time for students to create their target. Circulate and provide support as needed. Pay particular attention to the strategies students use to determine numbers and possible combinations.
| Possible Observations | Possible Interventions |
|---|---|
| Students do not know which numbers to choose to complete the target. |
Ask the following questions:
|
|
Some students form combinations that do not respect the distributive property. For example: \(\left( {28\; \times \;1} \right)\; = \;\left( {8\; \times \;1} \right)\, + \;\left( {5\; \times \;4} \right)\).  |
Ask them the following questions:
|
|
When choosing multiplier effects, some teams confuse the decomposition of a number as a sum with that of a number as a product. 
For example, they choose the numbers 2, 5 and 10 as multiplier effects and state that the combination of the three darts above is acceptable, that is: \(10 \times \;10 = \;\left( {10 \times \;2} \right)\; + \;\left( {10 \times \;5} \right)\). |
Ask them, for example:
Have them draw a rectangular layout that illustrates this number sentence and ask them the following question:

Note: Using the distributive property of multiplication over addition, the number 10 must be decomposed using a sum (for example, 1 + 9; 2 + 8; 3 + 7; 4 + 6) and not a product (for example, 2 x 5). |
|
Students have completed their target, but they can't write the combinations. 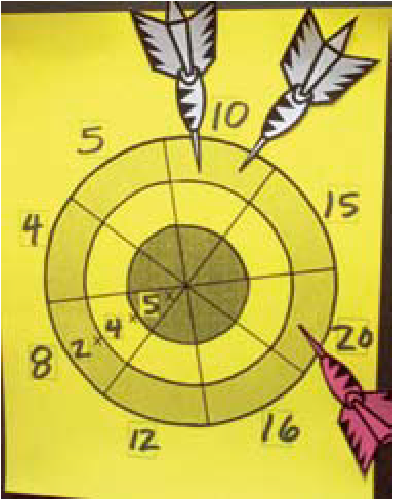 |
Ask the following question:
Then tell them to place the darts on the chosen numbers and to write down all the possible combinations as they go along, following the structure of the number sentences in the previous activity. |
When teams have completed the task, ask them to write down the combinations of the numbers they have chosen on a large sheet of paper. Tell students that the numbers must be legible from a distance and that the content of the chart must be clear and precise so that other students can understand their reasoning during the mathematical conversation.

Consolidation of Learning
Duration approximately 20 minutes
Ask a few teams to present their target and explain their approach with clear arguments based on terms of causality or logical consequence, such as:
- When I chose the numbers "x" and "y", I knew that I had to place the darts in the ring \(\times 2\) because the first dart is placed in that ring.
- First I scored 12 and 8 around our target. I then determined that the third number would be 20 since \(12\; + \;8\; = \;20\).
- Since the sum of two of the multiplier effects we have chosen (1 and 2) corresponds to the third multiplier effect (3), we automatically obtain 8 possible combinations, regardless of the numbers chosen for the sectors.
Invite other students to respond to each presentation with their observations or questions. Facilitate the mathematical conversation by asking questions as needed such as:
- Can anyone explain why the sum of the points obtained by the two given darts is equal to the number of points generated by the third dart?
- When looking for possible combinations, were there any that were easier to find? Which? For what ? [Students may mention that combinations related to place value decomposition [for example, \(12\; = \;10\; + \;2\)) or those related to doubles (for example, , \(12\; = \;6\; + \;6\)) were more obvious to them.]
- Which of the numbers around the target were placed first? How did you then choose the others?
- Did you have to change any of the numbers that did not combine? If so, which one(s)? What made you notice that the number(s) were not useful?
- Are there any combinations that have been overlooked? If so, which ones?
- Which version of the game (one or two darts) made it easier for you to find your combinations?
- How many winning combinations did you find?
The purpose of this mathematical conversation is to point out to students that the distributive property of multiplication is a very effective method of mental calculation.
Then suggest that students explain how this strategy can help them manipulate more difficult number facts (for example, \(15 \times \;4 = \;\left( {15 \times \;2} \right)\; + \;\left( {15 \times \;2} \right)\; = \;60\)) or to multiply a three-digit number by a two-digit number (for example, \(172\; \times \;12\; = \;\left( {172\; \times \;10} \right)\; + \;\left( {172\; \times \;2} \right)\) or \(\left( {100\; \times \;12} \right)\; + \;\left( {70\; \times \;12} \right)\; + \;\left( {2\; \times \;12} \right)\).
If necessary, demonstrate the connection between the distributive property of multiplication and the usual multiplication algorithm.
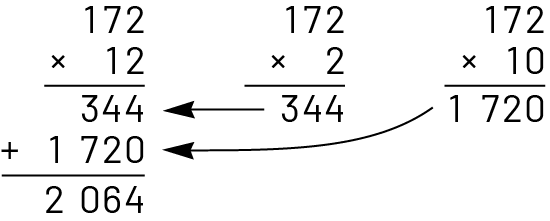
Note: At a convenient time, allow teams to exchange darts. This way, as they play, students apply and extend the distributive property as a mental math strategy.
Differentiated Instruction
The activity can be modified to meet the needs of the students.
| To Facilitate the Task | To Enrich the Task |
|---|---|
|
Examples 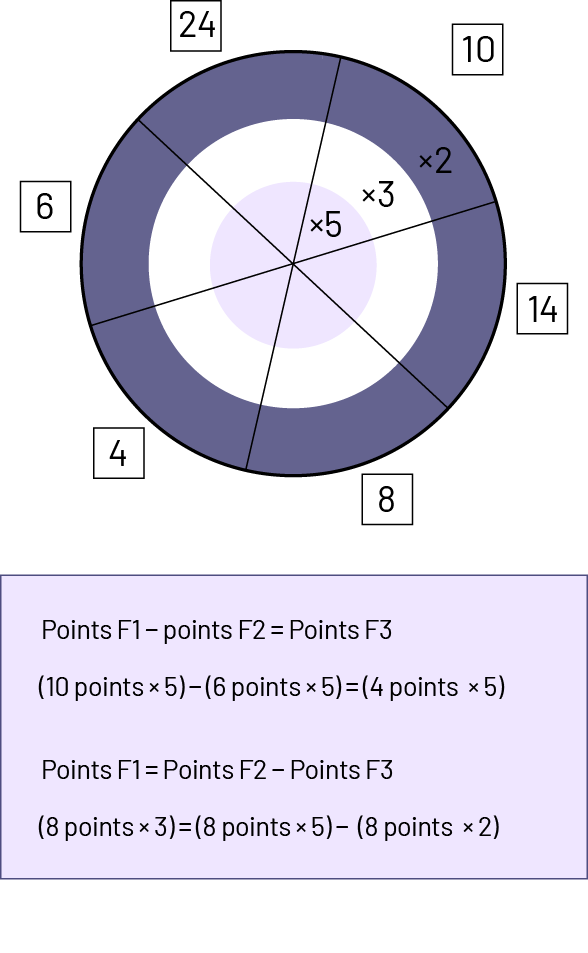 |
Follow-Up at Home
Ask students to take home the dartboard designed to play the game of darts. Instruct them on how to do this:
Explain the rules of the game to a family member.
Place one or two darts on the target depending on the version chosen.
Ask the person to place the corresponding dart(s) according to the rules of the game.
Check the solution.
Explain the use of the distributive property.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p 195-207.
