B1.2 Déterminer et représenter des carrés parfaits et calculer leur racine carrée, dans divers contextes.
Activité 1 : le concept de l’aire pour comprendre les carrés parfaits
Demander aux élèves de prendre une feuille quadrillée ou un tableau blanc quadrillé. Leur demander de dessiner 3 carrés de différentes dimensions (se limiter à des carrés de dimensions de \(12\; \times \;12\)).
Exemple
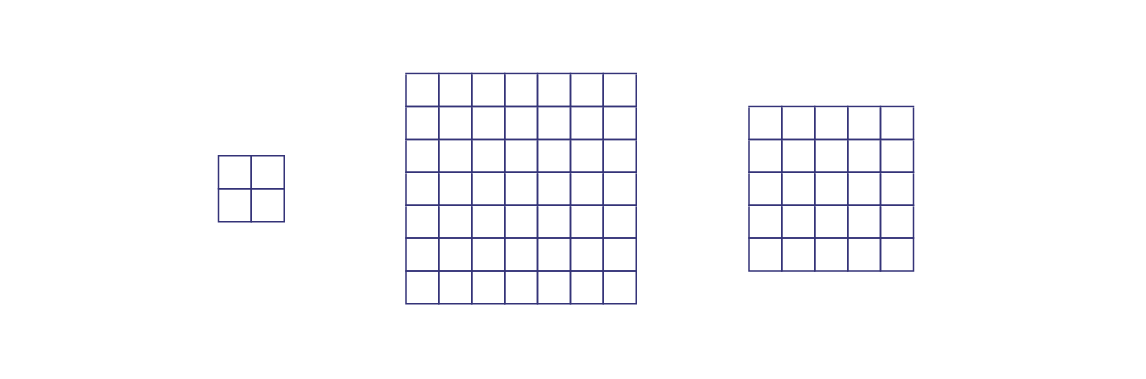
L’élève doit identifier les dimensions de chaque carré ainsi que leur aire respective.
Au besoin, activer les connaissances antérieures en lien avec l’aire du carré en leur posant cette question :
- Comment trouver l’aire d’un carré?
Les élèves devraient être en mesure d’établir le lien entre l’aire d’un carré et sa formule (base x hauteur).
Discuter avec les élèves des observations et de la signification des nombres carrés parfaits et des notations possibles afin de définir le concept.
Dans cette situation, les élèves devraient remarquer que les aires des carrés représentent les carrés parfaits ou les nombres carrés.
Activité 2 : les dimensions du carré pour introduire le concept de racine carrée
Afin de faire des liens avec l’activité de départ, donner l’aire d’un carré.
L’élève doit ensuite trouver une stratégie afin de trouver la longueur d’un des côtés du carré.
Discuter des propriétés du carré d’un nombre et introduire la racine carrée comme étant l’opération inverse du nombre élevé au carré. Par la suite, introduire le symbole de la racine carrée ainsi que la notation à utiliser.
Consolider les nouveaux apprentissages en leur demandant de calculer la racine carrée de carrés parfaits inférieurs à 144.
Activité 3 : trouver les carrés parfaits
Distribuer des cartes de nombres aléatoirement aux élèves (nombre sur les cartes de 0 à 150). L’élève devrait être en mesure de déterminer si ce nombre est un carré parfait (mettre de l’importance sur la justification de l’élève).
Pour vérifier la compréhension, si le nombre n’est pas un carré parfait, demander à l’élève entre quels 2 carrés parfaits se situe le nombre.
Exemple
Nombre sur la carte : 40
Ce nombre n’est pas un carré parfait, car 40 n’est pas le produit de 2 nombres naturels identiques. Il se situe entre les carrés parfaits 36 et 49.
