B1.2 Identify and represent perfect squares, and determine their square roots, in various contexts.
Activity 1: Using the Concept of Area to Understand Perfect Squares
Ask students to use a grid paper or whiteboard. Have them draw three squares of different sizes (limit to squares of size 12 by 12).
Example
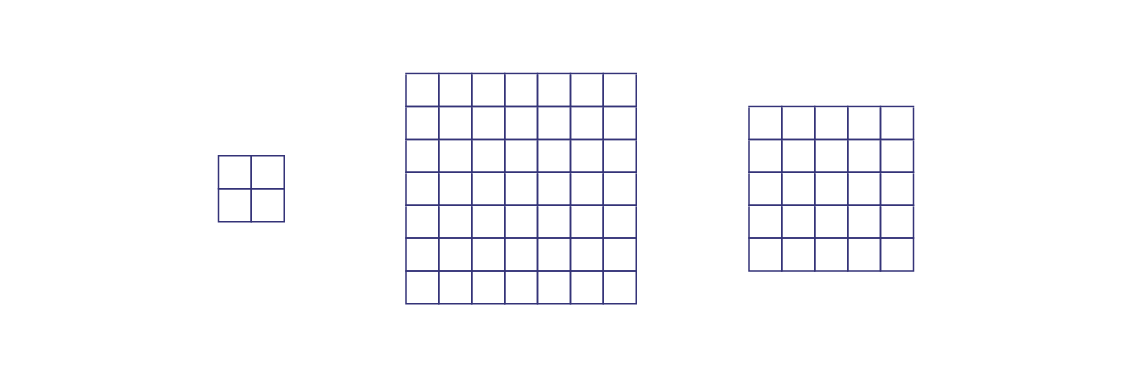
Ask students to identify the dimensions of each square and their respective areas.
If necessary, reactivate prior knowledge related to the area of the square by asking students:
- How do you find the area of a square?
Students should be able to relate the area of a square to its formula (base x height).
Discuss with students their observations and the meaning of perfect square numbers. Model proper notation to show the area of a perfect square.
In this situation, students should notice that the areas of the squares represent perfect squares or square numbers.
Activity 2: Using the Dimensions of the Square to Introduce the Concept of Square Root
In order to make connections with the original activity, give the area of a square.
The student must then devise a strategy to find the length of one of the sides of the square.
Discuss the properties of the square of a number and introduce the square root as the inverse operation of the squared number. Later, introduce the symbol for the square root as well as the notation to be used.
Consolidate new learning by asking students to calculate the square root of perfect squares less than 144.
Activity 3: Find the Perfect Squares
Randomly hand out number cards (with numbers from 0 to 150) to students. Ask them if their number is a perfect square and to justify their thinking.
If a student has a number that is not a perfect square, ask them which two perfect squares it falls between.
Example
Number on card: 40
This number is not a perfect square, because 40 is not the product of 2 identical whole numbers. It is between the perfect squares 36 and 49.
