B2.1 Utiliser les propriétés et la priorité des opérations et les relations entre les opérations pour résoudre des problèmes comportant des nombres naturels, des nombres décimaux, des fractions, des rapports, des taux et des pourcentages, y compris des problèmes à plusieurs étapes ou à plusieurs opérations.
Activité 1 : quel beau défi (priorité des opérations)
L’activité suivante représente un défi pour les élèves. Elle les incite à appliquer leurs connaissances de l’ordre des opérations et de l’effet des opérations sur les nombres. Les élèves doivent utiliser chacun des nombres d’une série donnée une seule fois, ainsi que quelques-unes des 4 opérations afin d’arriver le plus près possible d’un nombre cible. Par exemple, la suite de nombres est 2, 4, 5, 7, 10 et 25 et la cible est 433.
Exemple 1
\(\begin{align}10\; \times \;25\; &= \;250\\5\; \times \;7\; &= \;35\\250\; - \;35\; &= \;215\\215\; \times \;2\; &= \;430 \end{align}\)
430 + 4 = 434
Exemple 2
\(\begin{align}10\; \times \;7\; &= \;70\\70\; \times \;5\; &= \;350\\350\; + \;25\; &= \;375\\4\; + \;2\; &= \;6 \end{align}\)
375 + 6 = 381
Exemple 3
\(\begin{align}5\; \times \;7\; &= \;35\\10\; + \;2\; &= \;12\\35\; \times \;12\; &= \;420\\420\; + \;25\; &= \;445 \end{align}\)
445 - 4 = 441
Le niveau de difficulté de l’activité peut varier selon certaines modalités, à savoir :
- le choix des nombres – il peut être utile de fournir au moins 4 ou 5 nombres inférieurs à 10 et 2 ou 3 nombres qui facilitent les calculs (par exemple, 15, 25, 40, 50, 75, 100);
- l’utilisation des nombres – il faut déterminer si un nombre peut servir une seule fois ou à plusieurs reprises;
- le choix de la stratégie de calcul – sur papier, mentalement ou à l’aide de la calculatrice.
Si la priorité des opérations a fait l’objet d’une étude en classe, les élèves peuvent résumer leur solution à l’aide d’une phrase mathématique. Par exemple, elles et ils pourraient résumer leur solution ainsi \((5\; \times \;7)\; \times \;(10\; + \;2)\; + \;25\; - \;4\; = \;441\) pour l’exemple 3.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 110-111.
Pour aller plus loin
Faire cette même activité avec des nombres rationnels qui incluent des nombres décimaux et des fractions positives et négatives.
Exemple
Suite de nombres : (-20), (-10), (-0,5), \(\frac{1}{3}\), \(\frac{1}{2}\), 2, 40
Cible : 5
Exemple de réponse possible
\(\ ((40\; + \; (- 20 ))\; + \;(\frac{1}{2}\; \times \; (- 10))\; + \;2\; \times \; (- 0,5)) \; \times \;\frac{1}{3}\)
Réponse : \(\frac{{14}}{3}\; = \;4\frac{2}{3}\)
Activité 2 : que des trois!
L’activité suivante expose les élèves à l’utilisation de parenthèses pour préciser l’ordre des opérations dans une phrase mathématique. L’activité est conçue pour des élèves qui n’ont pas été préalablement exposés à la priorité des opérations. Si les élèves connaissent déjà la priorité des opérations ou savent comment utiliser les parenthèses, l’activité pourrait être menée différemment.
En groupe classe, dire aux élèves qu’il est possible de représenter le nombre 0 par une phrase mathématique en utilisant seulement le nombre 3 et une ou plusieurs des opérations arithmétiques. Leur donner un exemple en écrivant au tableau \(0\; = \;3\; - \;3\).
Leur présenter ensuite la phrase mathématique \(3\; \times \;3\; - \;3\; \times \;3\) et leur montrer que si on effectue les opérations dans l’ordre qu’elles apparaissent, on obtient 18 :
\(\begin{align}3\; \times \;3\; - \;3\; \times \;3\; &= \;9\; - \;3\; \times \;3\\ &= \;6\; \times \;3\\ &= \;18\end{align}\)
Cependant, si on effectue d’abord les 2 multiplications, on obtient 0 :
\(\begin{align}3\; \times \;3\; - \;3\; \times \;3\; &= \;9\; - \;9\\ &= \;0\end{align}\)
Il est aussi possible d’obtenir 0 en effectuant d’abord la soustraction :
\(\begin{align}3\; \times \;3\; - \;3\; \times \;3\; &= \;3 \times 0\; \times 3\\ &= \; 0 \times 3\\ &= \; 0\end{align}\)
Leur expliquer que par convention, on peut utiliser des parenthèses pour donner la priorité à l’une ou l’autre des opérations. Par exemple, si on veut donner la priorité aux 2 multiplications, on peut écrire \((3\; \times \;3)\; - \;(3\; \times \;3)\). Cependant, si on veut donner la priorité à la soustraction, on peut écrire \(3\; \times \;(3\; - \;3)\; \times \;3\).
Afin de s’assurer que les élèves ont bien compris, leur demander de représenter le nombre 1 par des phrases mathématiques en utilisant seulement le nombre 3 et une ou plusieurs opérations. Préciser qu’elles et ils doivent au besoin utiliser les parenthèses pour donner la priorité à l’une ou l’autre des opérations. Demander à quelques élèves d’écrire une phrase au tableau et demander aux autres d’en vérifier l’exactitude.
Voici quelques exemples de réponses possibles :
\(1 \; = 3 \div 3\) ou \(\frac{3}{3}\)
\(\begin{align} 1\; &= \;3\; - \;(3\; \div \;3)\; - \;(3 \div 3)\\ &= \; 3 \; -\; 1 \; - \;1 \\ &= \; 2 \; -\; 1 \\ &= \; 1 \end{align}\)
\(\begin{align} 1 \; &= \frac{{(3\; + \;3)}}{{(3\; + \;3)}} \\ \; &= \frac{6}{6} \\ \; &= \;1 \end{align}\)
Grouper les élèves par 2 et leur demander de présenter les nombres de 2 à 10 par différentes phrases mathématiques en utilisant le nombre 3, les 4 opérations et des parenthèses.
Une fois la tâche accomplie, demander à quelques élèves d’écrire, à tour de rôle, leurs phrases mathématiques au tableau et les regrouper selon le nombre en question.
Animer un échange mathématique et inviter les autres élèves à observer les phrases mathématiques et à en vérifier l’exactitude.
Note : Il est possible que certaines et certains élèves utilisent des parenthèses à l’intérieur des parenthèses. Dans de telles situations, il faut mentionner que la priorité est donnée d’abord aux parenthèses situées à l’intérieur des autres.
Exemple
\(\begin{align} 3\; - \;((3\; + \;3) \div \; 3 ) &= \; 3 \; - \;(6 \div 3) \\ &= \; 3 \; - \; 2 \\ &= \; 1\end{align}\)
Exemples de réponses possibles
\(2\; = \;(3\; + \;3)\; \div \;3\) ou \((3\; \div \;3)\; + \;(3\; \div \;3)\)
\(3\; = \;(3\; \times \;3)\; - \;(3\; + \;3)\) ou \((3\; + \;3)\; - \;3\)
\(4\; = \;3\; + \;(3\; \div \;3)\) ou \((3\; + \;3)\; - \;((3\; + \;3)\; \div \;3)\)
\(5\; = \;3\; + \;3\; - \;(3\; \div \;3)\) ou \((3\; \times \;3)\; - \;3\; - \;(3\; \div \;3)\)
\(6\; = \;3\; + \;3\) ou \((3\; \times \;3)\; - \;3\)
\(7\; = \;(3\; \times \;3)\; - \;\frac{{3\; + \;3}}{3}\) ou \((3\; + \;3)\; + \;(\;3\; \div \;3)\)
\(8\; = \;3\; + \;3\; + \;3\; - \;(3\; \div \;3)\) ou \(3\; + \;3\; + \;(3\; \div \;3)\; + \;(3\; \div \;3)\)
\(9\; = \;3\; + \;3\; + \;3\) ou \(3\; \times \;3\)
\(10\; = \;3\; + \;3\; + \;3\; + \;(3\; \div \;3)\) ou \((3\; \times \;3)\; + \;(3\; \div \;3)\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 209-211.
Pour aller plus loin
Faire le même exercice en utilisant des fractions ou des nombres décimaux.
Par exemple, leur demander de présenter les nombres de 1 à 10 par différentes phrases mathématiques en utilisant la fraction \(\frac{1}{2}\), les 4 opérations et des parenthèses.
Activité 3 : jouons avec les nombres (propriété de la distributivité de la multiplication)
Écrire au tableau ou sur une grande feuille de conférence, chacune des séries d’opérations apparentées suivantes, une à la fois, et demander aux élèves d’effectuer les opérations qu’elle contient.
| Série 1 | Série 2 | Série 3 | Série 4 |
|---|---|---|---|
|
\(\ 3\; \times \;6\) \(\ 3\; \times \;40\) \(\ 3\; \times \;46\) |
\(\ 2\; \times \;13\) \(\ 22\; \times \;10\) \(\ 22\; \times \;3\) \(\ 20\; \times \;13\) \(\ 22\; \times \;13\) |
\(\ 4 \times \;2\) \(\ 4 \times \;50\) \(\ 4 \times \;25\) \(\ 4 \times \;77\) |
\(\ 5\; \times \;5\) \(\ 5\; \times \;30\) \(\ 5\; \times \;100\) \(\ 5\; \times \;95\) |
Une fois une série complétée, faire ressortir les diverses stratégies de calcul mental en posant des questions telles que :
- Comment avez-vous résolu la dernière opération?
- Pour résoudre la dernière opération, avez-vous utilisé certains éléments des opérations précédentes?
- Avez-vous résolu les opérations dans l’ordre?
Si nécessaire, avant d’effectuer la même démarche avec la série suivante, présenter d’autres exemples d’opérations apparentées similaires.
Si les élèves ont de la difficulté à voir et à mettre en application la distributivité de la multiplication pour résoudre la dernière opération de chaque série, les y amener en représentant ces opérations sous forme de dispositions rectangulaires.
Exemple
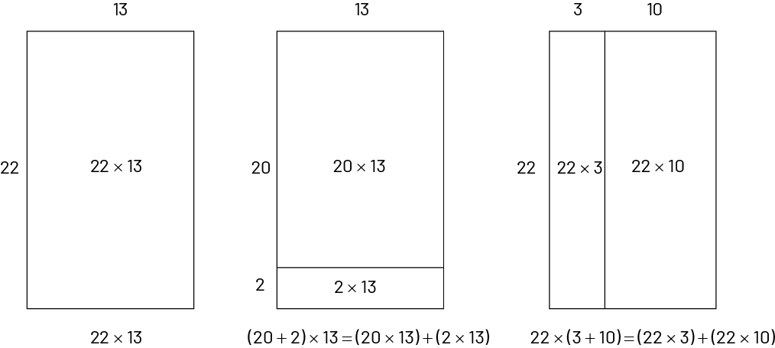Image Trois rectangles de la même grosseur sont présentés côte à côte. Dans le premier rectangle, il est écrit 22 fois
13. La largeur mesure 13, la longueur mesure 22. En dessous, il est
écrit 22 fois 13. Dans le deuxième rectangle, qui est divisé en deux, il est écrit vingt fois 13 dans la partie du
haut et vingt fois
13 dans la partie du bas. La largeur mesure 13, la longueur mesure vingt pour la première partie et deux pour la
deuxième partie. En dessous, il est écrit : parenthèse ouvrante vingt plus deux parenthèse fermante fois deux égale
parenthèse ouvrante vingt fois 13 parenthèse fermante plus parenthèse ouvrante deux fois 13 parenthèse fermante.Dans
le troisième rectangle, qui est divisé en deux, il est écrit 22 fois trois dans la partie de gauche et 22 fois
dix dans la partie de droite. La largeur mesure trois pour la première partie et dix pour la deuxième partie, et la
longueur mesure 22. En dessous, il est écrit : 22 fois parenthèse ouvrante trois plus dix parenthèse fermante égale
parenthèse ouvrante 22 fois trois parenthèse fermante plus parenthèse ouvrante 22 plus dix parenthèse fermante.
Constatations sur chacune des séries
Série 1
Cette série permet de revoir la propriété de distributivité de la multiplication sur l’addition à sa plus simple expression. Il s’agit de reconnaître que pour obtenir le produit de 3 × 46, il est possible d’effectuer une opération sur une somme de termes et d’obtenir le même résultat que si l’opération avait été effectuée sur chaque terme, c’est-à-dire :
\(\begin{align} 3\; \times \;46\; &= \;3\; \times \;(40 \; + \; 6)\\ &= \;(3 \times 40) \; + \;(3 \times 6)\end{align}\)
Série 2
Cette série permet de constater que la décomposition reliée à la distributivité peut s’effectuer aussi bien sur le second terme que sur le premier, soit :
\(22\; \times \;13\; = \;(20\; \times \;13)\; + \;(2\; \times \;13)\)
Ou
\(22\; \times \;13\; = \;(22\; \times \;3)\; + \;(22\; \times \;10)\)
Série 3
Cette série permet de constater que la décomposition d’un nombre pour appliquer la distributivité peut se faire en plus de 2 parties. Par exemple :
\(\begin{align}4\; \times \;77\; &= \;4\; \times \;(50\; + \;25\; + \;2)\\ &= \;(4\; \times \;50)\; + \;(4\; \times \;25)\; + \;(4\; \times \;2)\end{align}\)
Série 4
Cette série permet de constater que l’on peut résoudre la dernière opération à l’aide de la distributivité de la multiplication sur la soustraction. Par exemple :
\(\begin{align}5\; \times \;95\; &= \;5\; \times \;(100\; - \;5)\\ &= \;(5\; \times \;100)\; - \;(5\; \times \;5)\end{align}\)
Elle permet aussi de constater que l’on peut résoudre cette opération à l’aide de la distributivité de la multiplication sur l’addition et d’autres propriétés. Par exemple :
\(5\; \times \;95\; = \;3\; \times \;(5\; \times \;30)\; + (5\; \times \;5)\)
Pour aller plus loin : ajouter une série avec une fraction
| \(\frac{1}{4}\; \times \;40\) |
| \(\frac{1}{4}\; \times \;8\) |
| \(\frac{1}{4}\; \times \;1\) |
| \(\frac{1}{4}\; \times \;49\) |
\(\begin{align} \frac{1}{4}\; \times \;49\; &= \;\frac{1}{4}\;(40\; + \;8\; + \;1)\\ &= \;(\frac{1}{4}\; \times \;40)\; + \;(\frac{1}{4}\; \times \;8)\; + \;(\frac{1}{4}\; \times \;1)\\ &= \;10\; + \;2\; + \;\frac{1}{4}\\ &= \;12\frac{1}{4}\end{align}\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 221-222.
Activité 4 : qui dit la vérité? (propriété des nombres rationnels)
Présenter les règles du jeu qui consiste à présenter 3 énoncés dont 2 seront faux et l’autre vrai.
L’élève doit justifier à sa ou son partenaire (ou aux autres élèves de sa classe) pourquoi chaque énoncé est vrai ou faux.
Le but de l’activité est de déterminer laquelle ou lequel des élèves dit la vérité.
Note : L’élève n’a pas le droit à sa calculatrice.
Exemples d’énoncés
- Qui dit la vérité?
Élève 1 : \(5\; \times \;3\; - \;3\; \times \;4\; = \;0\)
Élève 2 : \(5\; \times \;3\; - \;3\; \times \;4\; = \;3\)
Élève 3 : \(5\; \times \;3\; - \;3\; \times \;4\; = \;48\)
Justifie.
- Qui dit la vérité?
Élève 1 : \(25\; \times \;40\; = \;(10\; \times \;40)\; + \;(10\; \times \;40)\; + \;(5\; \times \;40)\)
Élève 2 : \(25\; \times \;40\; = \;(20\; + \;40)\; \times \;(5\; + \;40)\)
Élève 3 : \(25\; \times \;40\; = \;(25\; \times \;4)\; + \;(25\; \times \;10)\)
Justifie.
- Qui dit la vérité?
Élève 1 : \((30\; - \;10)\; - \;5\; = \;30\; - \;(10\; - \;5)\)
Élève 2 : \((30\; - \;10)\; - \;5\; = \;30\; + \;((- 10)\; + \;5)\)
Élève 3 : \((30\; - \;10)\; - 5\; = \;30\; - \;(10\; + \;5)\)
Justifie.
- Qui dit la vérité?
Élève 1 : \((\frac{1}{2}\; \times \;0)\; + \;(0,5\; \times \;1)\; = \;0\)
Élève 2 : \((\frac{1}{2}\; \times \;0)\; + \;(0,5\; \times \;1)\; = 0,5\)
Élève 3 : \((\frac{1}{2}\; \times \;0)\; + \;(0,5\; \times \;1)\; = \;1\)
Justifie.
- Qui dit la vérité?
Élève 1 : \((50\;\% \; \times \;80)\; + \;(20\;\% \; \times \;80)\; = \;70\;\% \; \times \;160\)
Élève 2 : \((50\;\% \; \times \;80)\; + \;(20\;\% \; \times \;80)\; = \;70\;\% \; \times \;80\)
Élève 3 : \((50\;\% \; \times \;80)\; + \;(20\;\% \; \times \;80)\; = \;70\;\% \; \times \;6 400\)
Note : Construire les leurres à partir des erreurs fréquentes des élèves.