B2.1 Use the properties and order of operations, and the relationships between operations, to solve problems involving whole numbers, decimal numbers, fractions, ratios, rates, and percents, including those requiring multiple steps or multiple operations.
Activity 1: What a Great Challenge! (Order of Operations)
The following activity is a challenge for students. It challenges them to apply their knowledge of the order of operations and the effect of operations on numbers. Students must use each of the numbers in a given series only once, along with some of the four operations to get as close as possible to a target number. For example, the numbers are 2, 4, 5, 7, 10 and 25 and the target is 433.
Example 1
\(\begin{align}10\; \times \;25\; &= \;250\\5\; \times \;7\; &= \;35\\250\; - \;35\; &= \;215\\215\; \times \;2\; &= \;430\\430\; + \;4\; &= \;434\end{align}\)
Example 2
\(\begin{align}10\; \times \;7\; &= \;70\\70\; \times \;5\; &= \;350\\350\; + \;25\; &= \;375\\4\; + \;2\; &= \;6\\375\; + \;6\; &= \;381\end{align}\)
Example 3
\(\begin{align}5\; \times \;7\; &= \;35\\10\; + \;2\; &= \;12\\35\; \times \;12\; &= \;420\\420\; + \;25\; &= \;445\\445\; - \;4\; &= \;441\end{align}\)
The level of difficulty of the activity can vary according to certain modalities, namely:
- choice of numbers - it can be helpful to provide at least four or five numbers smaller than 10 and 2 or three numbers that make calculations easier (for example, 15, 25, 40, 50, 75, 100);
- the use of numbers - determine whether a number can be used once or repeatedly;
- choice of calculation strategy - on paper, mentally or with a calculator.
If the order of operations has been studied in class, students can summarize their solution with a number sentence. For example, they might summarize their solution as follows \((5\; \times \;7)\; \times \;(10\; + \;2)\; + \;25\; - \;4\; = \;441\) for Example 3.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 110-111.
Extensions
Do this same activity with rational numbers that include decimal numbers and positive and negative fractions.
Example
Sequence of numbers: - 20, - 10, - 0.5, \(\frac{1}{3}\), \(\frac{1}{2}\), 2, 40
Target: 5
Example of a possible answer
\(\ (40\; + \; - 20 )\; + \;(\frac{1}{2}\; \times \; - 10)\; + \;2\; \times \; - 0.5) \; \times \;\frac{1}{3}\)
Answer: \( - \frac{{14}}{3}\; = \;- 4\frac{2}{3}\)
Activity 2: Trios
The following activity introduces students to how brackets are used to specify the order of operations in a number sentence. The activity is designed for students who have not been previously introduced to the order of operations. If students are already familiar with the order of operations or know how to use brackets, the activity could be conducted differently.
As a class, tell students that it is possible to represent the number 0 in a number sentence using only the number 3 and one or more of the mathematical operations. Give them an example by writing on the board \(0\; = \;3\; - \;3\).
Then introduce the number sentence \(3\; \times \;3\; - \;3\; \times \;3\) and show them that if you do the operations in the order they appear, you get 18:
\(\begin{align}3\; \times \;3\; - \;3\; \times \;3\; &= \;9\; - \;3\; \times \;3\\ &= \;6\; \times \;3\\ &= \;18\end{align}\)
However, if we perform the 2 multiplications first, we get 0:
\(\begin{align}3\; \times \;3\; - \;3\; \times \;3\; &= \;9\; - \;9\\ &= \;0\end {align}\)
It is also possible to obtain 0 by first performing the subtraction:
\(\begin{align}3\; \times \;3\; - \;3\; \times \;3\; &= \;3 \times 0\; \times 3\\ &= \; 0 \times 3\\ &= \; 0\end{align}\)
Explain that brackets, like order of operations, are a convention that is used to ensure that such a problem is addressed in the same way by everyone. Brackets can be used to give priority to operations: the brackets signal that the operations within them are to be done first. For example, if one wants to give priority to the two multiplications, one can write \((3 \times \;3)\; - \;(3 \times \;3)\). However, if one wants to give the priority to the subtraction, one can write \(3\; \times \;(3\; - \;3)\times\;3\).
To ensure that students have understood, ask them to represent the number 1 in number sentences using only the number 3 and one or more operations. Point out that they should use brackets to give priority to one or more operations, if necessary. Ask a few students to write a sentence on the board and ask the others to check it for accuracy.
Examples of possible answers include:
\(1 \; = 3 \div 3\) or \(\frac{3}{3}\)
\(\begin{align} 1\; &= \;3\; - \;(3\; \div \;3)\; - \;(3 \div 3)\\ &= \; 3 \; -\; 1\; -\;1 \\ &= \; 2 \; -\; 1 \\ &= \; 1 \end{align}\)
\(\begin{align} 1 \; &= \frac{{(3\; + \;3)}}{{(3\; + \;3)}} \\ \; &= \frac{6 }{6} \\ \; &= \;1 \end{align}\)
Group students in pairs and ask them to present numbers from 2 to 10 in different number sentences using the number 3, the four operations and brackets.
Once the task is completed, ask a few students to take turns writing their number sentences on the board, grouping by the target number.
Select the work from a few groups that use strategies you'd like the class to see. When sharing each example, invite other students to observe the number sentences and check for accuracy.
Note: It is possible that some students use brackets within brackets. In such situations, it should be mentioned that priority is given to the brackets inside the others first.
Example
\(\begin{align} 3\; - \;((3\; + \;3) \div \; 3 ) &= \; 3 \; - \;(6 \div 3) \\ &= \; 3 \; - \; 2 \\ &= \; 1\end{align}\)
Examples of possible answers include:
\(2\; = \;(3\; + \;3)\; \div \;3\) or \((3\; \div \;3)\; + \;(3\; \div \;3)\)
\(3\; = \;(3\; \times \;3)\; - \;(3\; + \;3)\) or \((3\; + \;3)\; - \;3\)
\(4\; = \;3\; + \;(3\; \div \;3)\) or \((3\; + \;3)\; - \;((3\; + \;3)\; \div \;3)\)
\(5\; = \;3\; + \;3\; - \;(3\; \div \;3)\) or \((3\; \times \;3)\; - \; 3\; - \;(3\; \div \;3)\)
\(6\; = \;3\; + \;3\) or \((3\; \times \;3)\; - \;3\)
\(7\; = \;(3\; \times \;3)\; - \;\frac{{3\; + \;3}}{3}\) or \((3\; + \;3)\; + \;(\;3\; \div \;3)\)
\(8\; = \;3\; + \;3\; + \;3\; - \;(3\; \div \;3)\) or \(3\; + \;3\; + \;(3\; \div \;3)\; + \;(3\; \div \;3)\)
\(9\; = \;3\; + \;3\; + \;3\) or \(3\; \times \;3\)
\(10\; = \;3\; + \;3\; + \;3\; + \;(3\; \div \;3)\) or \((3\; \times \;3 )\; + \;(3\; \div \;3)\)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 209-211.
Extensions
Do the same exercise using fractions or decimal numbers.
For example, ask students to present numbers from 1 to 10 in different number sentences using the fraction \(\frac{1}{2}\), the four operations and brackets.
Activity 3: Let's Play With Numbers (Distributive Property of Multiplication)
Write each of the following sets of related operations, one at a time, on the board or a large piece of flip chart paper and have students perform the operations in it.
| Set 1 | Set 2 | Set 3 | Set 4 |
|---|---|---|---|
|
\( 3 \times 6\) \(3 \times 40 \) \(3 \times 46 \) |
\(2 \times 13\) \(22 \times 10\) \(22 \times 3\) \( 20 \times 13\) \(\ 22\; \times \;13\) |
\(4 \times 2\) \( 4 \times 50\) \( 4 \times 25\) \(\ 4 \times \;77\) |
\(5 \times 5\) \(5 \times 30\) \(5 \times 100\) \(5 \times 95\) |
Once a set is completed, draw out the various mental math strategies by asking questions such as:
- How did you solve the last operation?
- To solve the last operation, did you use any elements of the previous operations?
- Did you solve the operations in order?
If necessary, before doing the same with the next set, present other examples of similar related operations.
If students have difficulty seeing and applying the distributive property of multiplication to solve the last operation in each set, lead them to do so by representing these operations as area models.
Example
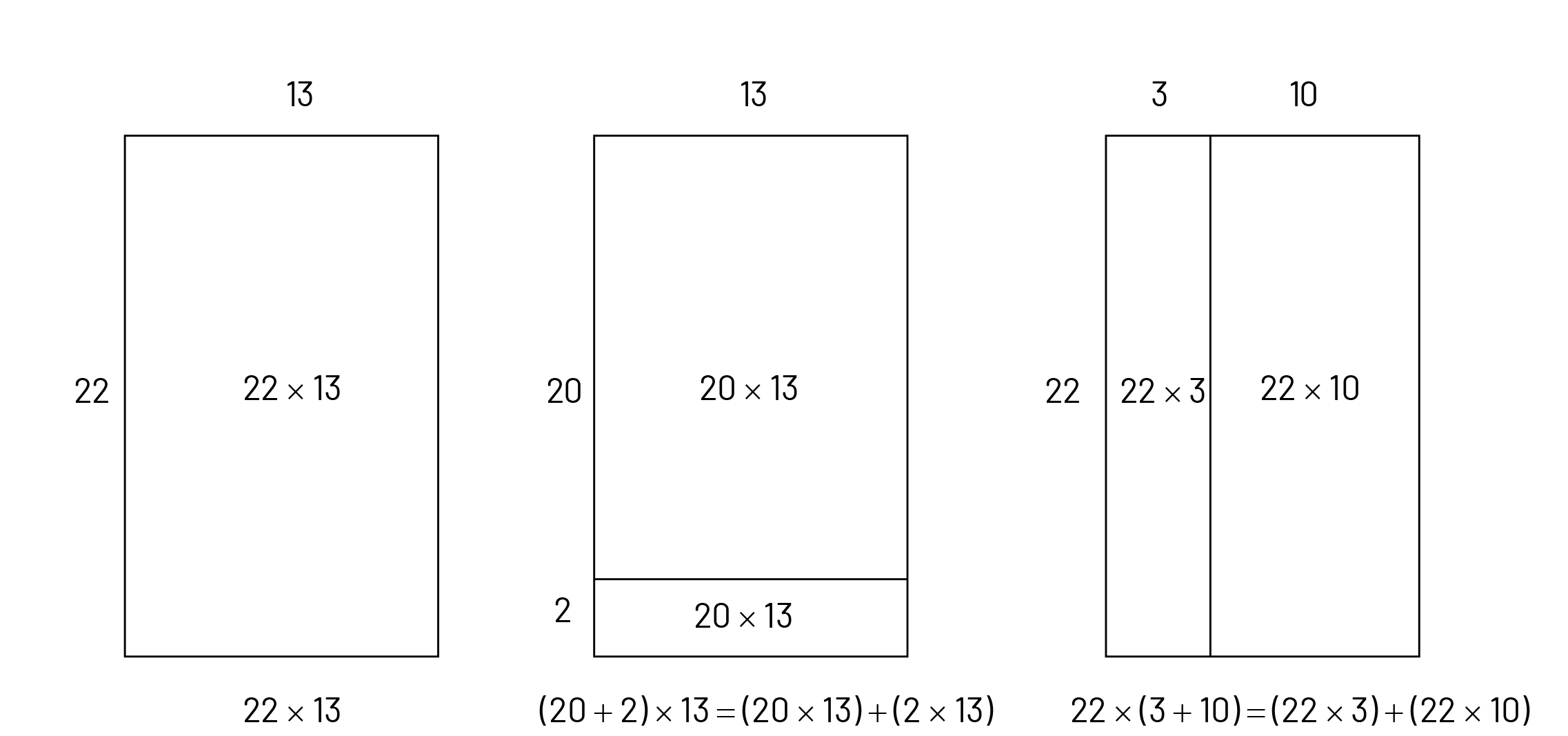
Findings for Each Set
Set 1
This set demonstrates a simple application of the distributive property of multiplication over addition. The idea is to recognize that to obtain the product of 3 × 46, it is possible to perform the operation ×3 on each term and then sum the results:
\(\begin{align} 3\; \times \;46\; &= \;3\; \times \;(40 \; + \; 6)\\ &= \;(3 \times 40) + \;(3 \times 6)\end{align}\)
Set 2
This set demonstrates that when using the distributive property, decomposition can be done on either term:
\(22\; \times \;13\; = \;(20\; \times \;13)\; + \;(2\; \times \;13)\)
Or
\(22\; \times \;13\; = \;(22\; \times \;3)\; + \;(\;22\; \times \;10)\)
Set 3
This set demonstrates how the decomposition of a number to apply the distributive property can be done in more than two parts. For example:
\(\begin{align}4\; \times \;77\; &= \;4\; \times \;(50\; + \;25\; + \;2)\\ &= \;(4\; \times \;50)\; + \;(4\; \times \;25)\; + \;(4\; \times \;2)\end{align}\)
Set 4
This set demonstrates how we can decompose a term using subtraction and then apply the distributive property of multiplication. For example:
\(\begin{align}5\; \times \;95\; &= \;5\; \times \;(100\; - \;5)\\ &= \;(5\; \times \;100)\; - \;(5\; \times \;5)\end{align}\)
It also shows that this expression can be solved by using the distributive property of multiplication over addition and other properties. For example:
\(5\; \times \;95\; = (5\; \times \;30) \times\;3 \;+ (5\; \times \;5)\)
To go further: add a set with a fraction
| \(\frac{1}{4} \times 40\) |
| \(\frac{1}{4} \times 8\) |
| \(\frac{1}{4} \times 1\) |
| \(\frac{1}{4} \times 49\) |
\(\begin{align} \frac{1}{4}\; \times \;49\; &= \;\frac{1}{4}\;(40\; + \;8\; + \;1)\\ &= \;(\frac{1}{4}\; \times \;40)\; + \;(\frac{1}{4}\; \times \;8)\; + \;(\frac{1}{4}\; \times \;1)\\ &= \;10\; + \;2\; + \;\frac{1}{4}\\ &= \;12\frac{1}{4}\end{align}\)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Fascicule 1, Nombres naturels, p. 221-222.
Activity 4: Who is Telling the Truth? (Property of Rational Numbers)
Introduce the rules of the game which involve three students presenting three statements. Two will have false statements and one will have a true statement.
The students must justify to their group (or other students in the class) why each statement is true or false.
The purpose of the activity is to determine which student is telling the truth.
Note: The students should not use a calculator.
Construct the decoys based on common student errors.
Examples of statements
- Who is telling the truth?
Student 1: \(5\; \times \;3\; - \;3\; \times \;4\; = \;0\)
Student 2: \(5\; \times \;3\; - \;3\; \times \;4\; = \;3\)
Student 3: \(5\; \times \;3\; - \;3\; \times \;4\; = \;48\)
Justify.
- Who is telling the truth?
Student 1: \(25\; \times \;40\; = \;(10\; \times \;40)\; + \;(10\; \times \;40)\; + \;(5 \; \times \;40)\)
Student 2: \(25\; \times \;40\; = \;(20\; + \;40)\; \times \;(5\; + \;40)\)
Student 3: \(25\; \times \;40\; = \;(25\; \times \;4)\; + \;(25\; \times \;10)\)
Justify.
- Who is telling the truth?
Student 1: \((30 - \;10)\; - \;5 = \;30 - \;(10 - \;5)\)
Student 2: \((30\; - \;10)\; - \;5\; = \;30\; + \;( - 10\; + \;5)\)
Student 3: \((30 - \;10)\; - 5 = \;30 - \;(10 + \;5)\)
Justify.
- Who is telling the truth?
Student 1: \((\frac{1}{2}\; \times \;0)\; + \;(0.5\; \times \;1)\; = \;0\)
Student 2: \((\frac{1}{2}\; \times \;0)\; + \;(0.5\; \times \;1)\; = 0.5\)
Student 3: \((\frac{1}{2}\; \times \;0)\; + \;(0.5\; \times \;1)\; = \;1\)
Justify.
- Who is telling the truth?
Student 1: \((50\% \; \times \;80)\; + \;(20\% \; \times \;80)\; = \;70\% \; \times \;160\)
Student 2: \((50\% \; \times \;80)\; + \;(20\% \; \times \;80)\; = \;70\% \; \times \;80\)
Student 3: \((50\% \; \times \;80)\; + \;(20\% \; \times \;80)\; = \;70\% \; \times \;6 400\)
