B1.2 Déterminer et représenter des carrés parfaits et calculer leur racine carrée, dans divers contextes.
Habileté : représenter des carrés parfaits
Afin de représenter un carré parfait, l’élève construit un carré et indique la longueur des côtés (longueur et largeur). Le carré parfait représente l’aire du carré.
Exemples

Le carré parfait est représenté par \(5\; \times \;5\; = \;{5^2}\; = \;25\)
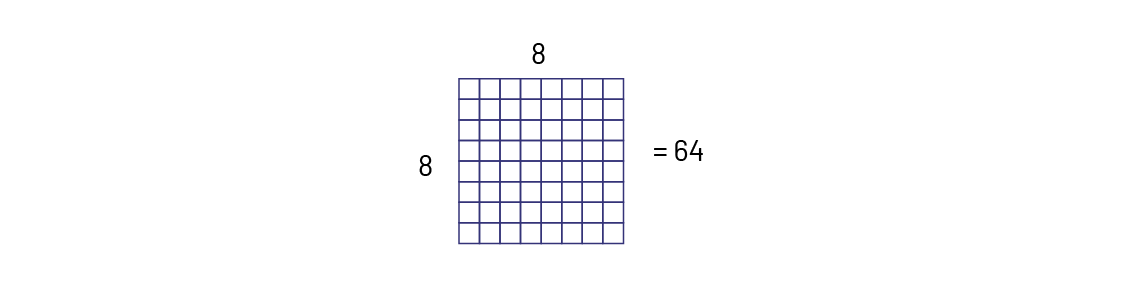
Le carré parfait est représenté par \(8\; \times \;8\; = \;{8^2}\; = \;64\)
Habileté : déterminer les carrés parfaits
L’élève devrait être en mesure de décomposer des nombres. Par exemple, 49 peut être décomposé comme étant le produit de \(7\; \times \;7\).
Afin de déterminer un carré parfait, l’élève construit un tableau avec les nombres naturels de 1 à 12. En multipliant chaque nombre naturel par lui-même, il obtient les carrés parfaits. Ainsi, l’élève peut représenter un carré parfait en prenant un nombre naturel comme base et en l’élevant au carré (exposant de 2).
| Nombre naturel | Forme développée | Forme exponentielle | Forme symbolique |
|---|---|---|---|
| 1 | \(1\; \times \;1\) | \({1^2}\) | 1 |
| 2 | \(2\; \times \;2\) | \({2^2}\) | 4 |
| 3 | \(3\; \times \;3\) | \({3^2}\) | 9 |
| 4 | \(4\; \times \;4\) | \({4^2}\) | 16 |
| 5 | \(5\; \times \;5\) | \({5^2}\) | 25 |
| 6 | \(6\; \times \;6\) | \({6^2}\) | 36 |
| 7 | \(7\; \times \;7\) | \({7^2}\) | 49 |
| 8 | \(8\; \times \;8\) | \({8^2}\) | 64 |
| 9 | \(9\; \times \;9\) | \({9^2}\) | 81 |
| 10 | \(10\; \times \;10\) | \({10^2}\) | 100 |
| 11 | \(11\; \times \;11\) | 112 | 121 |
| 12 | \(12\; \times \;12\) | 122 | 144 |
Les élèves doivent connaître les carrés parfaits les plus communs tels que 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 225 et 400 et leurs racines carrées associées.
\(\)
Habileté : calculer la racine carrée de carrés parfaits
Puisque la racine carrée est l’opération inverse d’élever un nombre au carré, l’élève construit un tableau avec tous les carrés parfaits et peut ainsi trouver sa racine carrée en décomposant le carré parfait (le nombre naturel initial multiplié par lui-même). La racine carrée représente donc le nombre naturel d’origine.
| Nombre carré parfait | Forme développée | Forme exponentielle | Racine carrée |
|---|---|---|---|
| 1 | \(1\; \times \;1\) | \({1^2}\) | 1 |
| 4 | \(2\; \times \;2\) | \({2^2}\) | 2 |
| 9 | \(3\; \times \;3\) | \({3^2}\) | 3 |
| 16 | \(4\; \times \;4\) | \({4^2}\) | 4 |
| 25 | \(5\; \times \;5\) | \({5^2}\) | 5 |
| 36 | \(6\; \times \;6\) | \({6^2}\) | 6 |
| 49 | \(7\; \times \;7\) | \({7^2}\) | 7 |
| 64 | \(8\; \times \;8\) | \({8^2}\) | 8 |
| 81 | \(9\; \times \;9\) | \({9^2}\) | 8 |
| 100 | \(10\; \times \;10\) | \({10^2}\) | 10 |
| 121 | \(11\; \times \;11\) | \({11^2}\) | 11 |
| 144 | \(12\; \times \;12\) | \({12^2}\) | 12 |
De façon symbolique, la racine carrée d’un nombre s’écrit avec le symbole  avec le nombre sous le symbole.
avec le nombre sous le symbole.
Ainsi, la racine carrée de 1 peut s’écrire comme
\(\frac{1}{{\sqrt 1 }}\; = \;\frac{{1\; \times \;1}}{{\sqrt {1 \; \times \;1}}}\)
= 1 et la racine carrée de 36 peut s’écrire comme
\(\frac{{36}}{{\sqrt {36} }}\; = \;\frac{{6\; \times \;6}}{{\sqrt {6 \; \times \;6}}}\)
= 6.
Note : La racine carrée d’un nombre élevé au carré (forme exponentielle) est représentée par la base du nombre.
De façon visuelle, la racine carrée peut s’obtenir en trouvant la longueur d’un côté avec une aire donnée.
Par exemple, l’aire du carré est 144 unités carrées

Donc, la racine carrée de 144 est 12, car la longueur des côtés qui donne l’aire de 144 est 12 unités par 12 unités.
Source : En avant, les maths! 7e année, CM, Nombres, p. 3-4.
Connaissance : représentation d’un carré parfait
Un nombre naturel multiplié par lui-même produit un nombre carré, ou un carré parfait, et peut être représenté par une puissance avec un exposant de 2. Par exemple, 9 est un nombre carré parce que \(3\; \times \;3\; = \;9\) ou 32.
Voici 3 façons d’écrire le carré parfait 9 :
- La forme symbolique : 9
- La forme développée : \(3\; \times \;3\)
- La forme exponentielle : 32
La racine carrée d’un nombre rationnel positif est toujours positive. La racine carrée d’un nombre rationnel négatif n’existe pas dans les nombres réels.
L’opération inverse de calculer le carré d’un nombre est de calculer sa racine carrée. La racine carrée de 9 (ou 9) est 3.
Les carrés et les racines carrées sont des opérations inverses.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
L’aire d’un carré est égale au produit de la mesure de sa base par sa hauteur. De plus, dans un carré la mesure de la base est égale à celle de la hauteur. Par conséquent, l’aire du carré peut être exprimée par la formule \(\ A\; = \;{\rm{mesure \;\;\; du \;\;côté \;\;\; 1}}\; \times \;{\rm{mesure \;\;\; du \;\; côté \;\;\; 2}}\) ou \(\ A = c \; \times c = c\;^2\).
