B1.2 Identify and represent perfect squares, and determine their square roots, in various contexts.
Skill: Representing Perfect Squares
To represent a perfect square, the student constructs a square and indicates the length of the sides (length and width). The perfect square number represents the area of the square.
Examples

The perfect square is represented by \(5 \times 5 = {5^2} = 25 \)
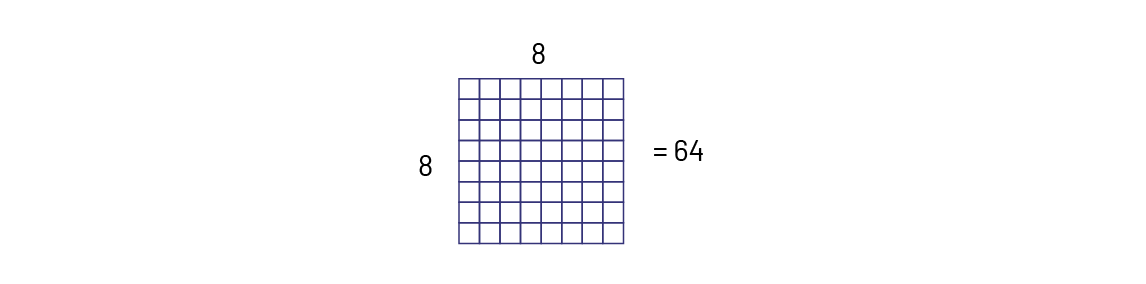
The perfect square is represented by \(8 \times 8 = {8^2} = 64 \)
Skill: Determining Perfect Squares
Students should be able to decompose numbers. For example, 49 can be decomposed as the product of \(7\; \times \;7\).
To determine a perfect square, ask students to construct a table with whole numbers from 1 to 12. By multiplying each whole number by itself, they obtain the perfect square numbers. Thus, the student can represent a perfect square by taking a whole number as a base and squaring it (exponent of 2).
| Whole Number | Dimensions | Exponential Form | Perfect Square Number |
|---|---|---|---|
| 1 | \(1\; \times \;1\) | \({1^2}\) | 1 |
| 2 | \(2\; \times \;2\) | \({2^2}\) | 4 |
| 3 | \(3\; \times \;3\) | \({3^2}\) | 9 |
| 4 | \(4\; \times \;4\) | \({4^2}\) | 16 |
| 5 | \(5\; \times \;5\) | \({5^2}\) | 25 |
| 6 | \(6\; \times \;6\) | \({6^2}\) | 36 |
| 7 | \(7\; \times \;7\) | \({7^2}\) | 49 |
| 8 | \(8\; \times \;8\) | \({8^2}\) | 64 |
| 9 | \(9\; \times \;9\) | \({9^2}\) | 81 |
| 10 | \(10\; \times \;10\) | \({10^2}\) | 100 |
| 11 | \(11\; \times \;11\) | 112 | 121 |
| 12 | \(12\; \times \;12\) | 122 | 144 |
Students should know the most common perfect squares such as 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 225 and 400 and their associated square roots.
\(\)
Skill: Calculating the Square Root of Perfect Squares
Since the square root is the inverse operation of squaring a number, the student builds a table with all the perfect squares and can thus find its square root by decomposing the perfect square (the original whole number multiplied by itself). The square root thus represents the original whole number.
| Perfect Square Number | Dimensions | Exponential Form | Square Root |
|---|---|---|---|
| 1 | \(1\; \times \;1\) | \({1^2}\) | 1 |
| 4 | \(2\; \times \;2\) | \({2^2}\) | 2 |
| 9 | \(3\; \times \;3\) | \({3^2}\) | 3 |
| 16 | \(4\; \times \;4\) | \({4^2}\) | 4 |
| 25 | \(5\; \times \;5\) | \({5^2}\) | 5 |
| 36 | \(6\; \times \;6\) | \({6^2}\) | 6 |
| 49 | \(7\; \times \;7\) | \({7^2}\) | 7 |
| 64 | \(8\; \times \;8\) | \({8^2}\) | 8 |
| 81 | \(9\; \times \;9\) | \({9^2}\) | 8 |
| 100 | \(10\; \times \;10\) | \({10^2}\) | 10 |
| 121 | \(11\; \times \;11\) | \({11^2}\) | 11 |
| 144 | \(12\; \times \;12\) | \({12^2}\) | 12 |
Symbolically, the square root of a number is written with the symbol  with the number under the symbol.
with the number under the symbol.
Thus, the square root of 1 can be written as
\(\frac{1}{{\sqrt 1 }}\; = \;\frac{{1\; \times \;1}}{{\sqrt 1 \; \times \;1}}\)
= 1 and the square root of 36 can be written as
\(\frac{{36}}{{\sqrt {36} }}\; = \;\frac{{6\; \times \;6}}{{\sqrt 6 \; \times \;6}}\)
= 6.
Note: The square root of a squared number (exponential form) is represented by the base of the number.
Example
\(\frac{{49}}{{\sqrt {49} }}\)
= 7
Visually, the square root can be obtained by finding the length of a side of a square with a given area.
For example, the area of the square is 144 square units.

Therefore, the square root of 144 is 12, because the length of the sides that gives the area of 144 is 12 units by 12 units.
Source: translated from En avant, les maths! 7e, Nombres, p. 3-4.
Knowledge: Representation of a Perfect Square
Any whole number multiplied by itself produces a square number, or a perfect square, and can be represented as a power with an exponent of 2. For example, 9 is a square number because \(3\; \times \;3\; = \;9\) or \(3^2\).
Here are 3 ways to write the perfect square 9:
- The symbolic form: 9
- The expanded form: \(3\; \times \;3\)
- The exponential form: 32
The square root of a positive rational number is always positive. The square root of a negative rational number does not exist in real numbers.
The inverse of squaring a number is to take its square root. The square root of 9 (or 9) is 3.
Squares and square roots are inverse operations.
Source: Ontario Curriculum. Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
A perfect square can be represented as a square with an area equal to the value of the perfect square. The side length of a perfect square is the square root of its area. In general, the area (A) of a square is \(\ A\; = measure \;\;\; from \;\;\;side \;\;\; 1\; \times \;\;measure \;\;\; on \;\;\; the \;\;\; side \;\;\; 2\) or \(\ A\; = \;\;c\; \times \;\;c\; = \;{c^2}\).
