B2.5 Additionner et soustraire des fractions, en utilisant des stratégies appropriées, dans divers contextes.
Activité 1 : manger en groupe (addition et soustraction de fractions)
Matériel
- matériel de manipulation qui peut aider à la compréhension des opérations sur les fractions (bandes fractionnaires, cercles fractionnaires, réglettes, jetons)
- papier quadrillé
Diviser le groupe classe en équipes de 4 élèves.
Préparer des fiches avec des situations en lien avec la nourriture.
Chaque équipe se rend à une station afin de résoudre le problème écrit sur la fiche.
Gérer le temps de travail et faire une rotation lorsque le temps est opportun.
Suggestions pour le retour
Demander à 2 équipes par station de vous envoyer une photo de leur travail.
Les membres des deux équipes choisies présentent leur démarche de résolution.
Mettre l’importance sur la démarche et la compréhension.
Questionner les élèves lors de la présentation.
Exemples de problème sur les fiches
- Ginette et Marc partagent une barre de chocolat. Ginette en a mangé \(\frac{1}{3}\) et Marc lui en a mangé la moitié. Quelle fraction de la tablette reste-t-il?
- Zachary fait 4 sortes de biscuits pour une vente de pâtisseries afin d’amasser des fonds pour son voyage de 8e année. Chaque recette demande de la farine.
- Un groupe d’élèves se préparent à commander des pizzas de 9 pouces pour une fête.
Biscuits aux pépites de chocolat : \(1\frac{1}{2}\) tasses
Biscuits à l’avoine : \(\frac{3}{4}\) de tasse
Biscuits au sucre : \(\frac{2}{3}\) de tasse
Biscuits à mélasse : \(2\frac{1}{4}\) tasses
Quelle quantité de farine a-t-il besoin afin d’être capable de faire les 4 sortes de biscuits?
Mohammed veut \(\frac{1}{2}\) d’une pizza.
Katrina veut \(\frac{1}{3}\) d’une pizza
Gigi veut \(\frac{5}{6}\) d’une pizza
Axel veut \(\frac{3}{4}\) d’une pizza
Vlad veut \(\frac{3}{8}\) d’une pizza
Combien de pizzas sont nécessaires? Est-ce qu’il va en rester? Si oui, quelle fraction?
Activité 2 : casse-tête des fractions (addition et soustraction)
Diviser le groupe classe en équipes de 4 élèves.
Chaque équipe construit un casse-tête d’expressions contenant des additions et des soustractions sur les fractions.
Distribuer un gabarit (tableau vierge de \(4\; \times \;4\)) comme ici-bas.
L’élève doit s’assurer d’écrire, pour chaque segment commun, une expression avec sa réponse.
Par exemple, \(\frac{3}{4}\; - \;\frac{1}{2}\; + \;\frac{1}{4}\)(expression) et \(\frac{1}{2}\) (réponse de l’expression) doivent être de part et d’autre d’un segment commun (voir tableau).
Image Un
carré est divisé en 16 carrés égaux. Dans le deuxième carré de la première rangée, il est écrit un demi. Et dans le
deuxième carré de la deuxième rangée, il est écrit trois quarts moins un demi plus un quart.
Une fois terminé, le tableau de chaque équipe devrait ressembler à ceci.
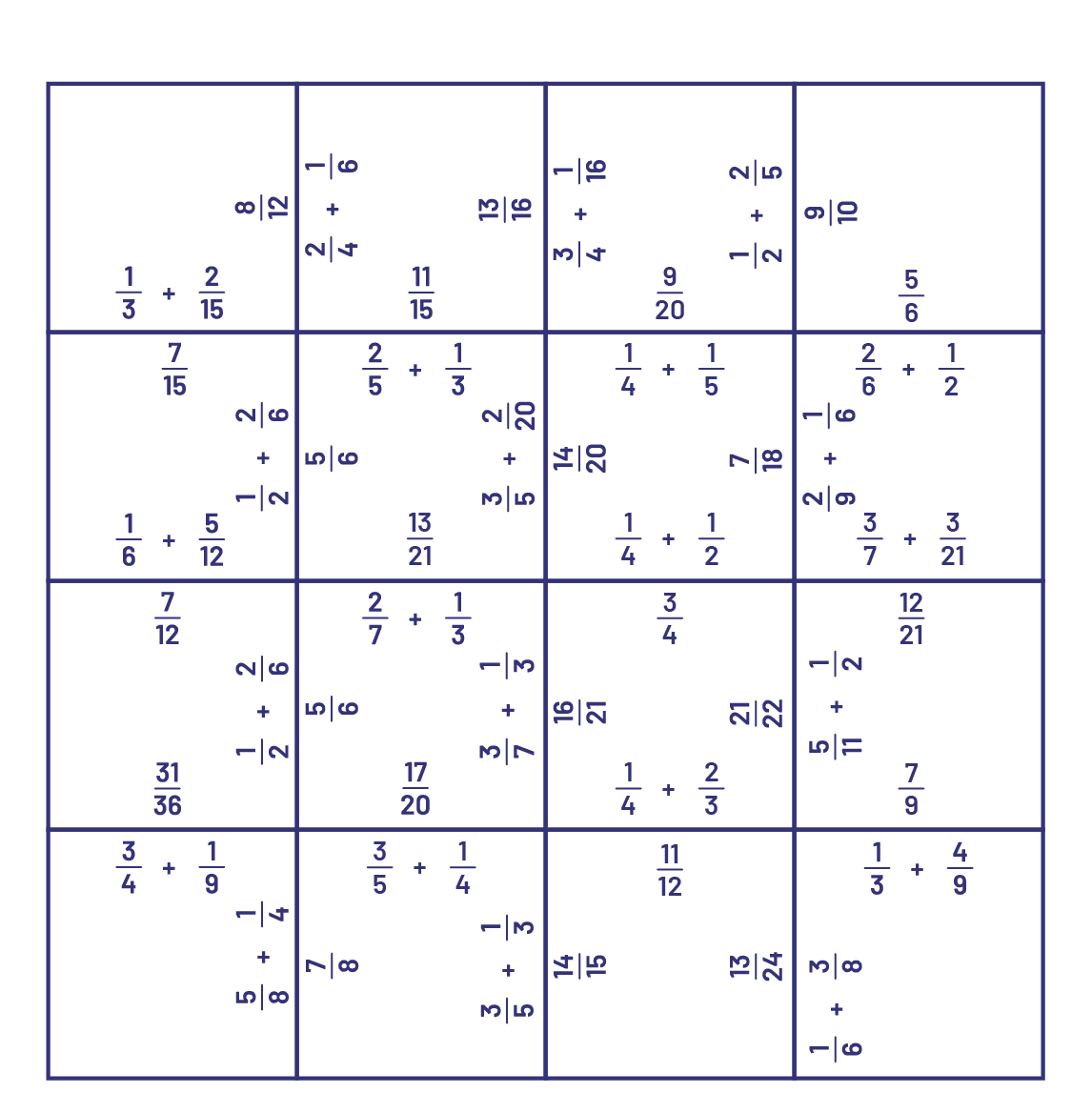Image Carré divisé en 16. La description va de gauche à droite et de haut en bas. Dans le premier carré, il est écrit
un tiers plus deux quinzièmes au-dessus de la base; et huit douzième est écrit
de côté vis-à-vis le côté droit. Dans le deuxième carré, il est écrit deux quarts plus un sixième, de côté,
vis-à-vis le côté gauche; onze quinzièmes au-dessus de la base; et treize seizièmes est écrit de côté vis-à-vis le
côté droit. Dans le troisième carré, il est écrit trois quarts plus un seizième de côté vis-à-vis le côté gauche;
neuf vingtièmes au-dessus de la base; et un demi plus deux cinquièmes de côté vis-à-vis le côté droit. Dans le
quatrième carré, il est écrit neuf dixièmes de côté vis-à-vis le côté gauche; et cinq sixièmes au-dessus de la base.
Dans le cinquième carré, il est écrit sept quinzièmes sous le côté du haut; un sixième plus cinq douzièmes
au-dessus de la base; et un demi plus deux sixièmes de côté vis-à-vis le côté droit. Dans le sixième carré, il est
écrit cinq sixièmes de côté vis-à-vis le côté gauche; deux cinquièmes plus un tiers sous le côté du haut; treize
vingt et unièmes au-dessus de la base; et trois cinquièmes plus deux vingtièmes de côté vis-à-vis le côté droit.
Dans le septième carré, il est écrit quatorze vingtièmes de côté vis-à-vis le côté gauche; un quart plus un
cinquième sous le côté du haut; un quart plus un demi au-dessus de la base; et sept dix-huitièmes de côté vis-à-vis
le côté droit. Dans le huitième carré, il est écrit deux neuvièmes plus un sixième de côté vis-à-vis le côté gauche;
deux sixièmes plus un demi sous le côté du haut; et trois septièmes plus trois vingt et unièmes au-dessus de la
base.Dans le neuvième carré, il est écrit sept douzièmes sous le côté du haut; 31 trente-sixièmes au-dessus de la
base; et un demi plus deux sixièmes sur le côté vis-à-vis le côté droit. Dans le dixième carré, il est écrit cinq
sixièmes de côté vis-à-vis le côté gauche; deux septièmes plus un tiers sous le côté du haut; 17 vingtièmes au-dessus
de la base; et trois septièmes plus un tiers de côté vis-à-vis le côté droit. Dans le dixième carré, il est écrit cinq
sixièmes de côté vis-à-vis le côté gauche; deux septièmes plus un tiers sous le côté du haut; 17 vingtièmes
au-dessus de la base; et trois septièmes plus un tiers de côté vis-à-vis le côté droit. Dans l'onzième carré, il est
écrit 16 vingt et unièmes de côté vis-à-vis le côté gauche; trois quarts sous le côté du haut; un quart plus deux
tiers au-dessus de la base; et 21 vingt-deuxièmes de côté vis-à-vis le côté droit. Dans le douzième carré, il est
écrit cinq onzièmes plus un demi de côté vis-à-vis le côté gauche; douze vingt et unièmes sous le côté du haut; et
sept neuvièmes au-dessus de la base.Dans le treizième carré, il est écrit trois quarts plus un neuvième sous le côté
du haut; et cinq huitièmes plus un
quart de côté vis-à-vis le côté droit. Dans le quatorzième carré, il est écrit sept huitièmes de côté vis-à-vis le
côté gauche; trois cinquièmes plus un quart sous le côté du haut; et trois cinquièmes plus un tiers de côté
vis-à-vis le côté droit. Dans le quinzième carré, il est écrit 14 quinzièmes de côté vis-à-vis le côté gauche; onze
douzièmes sous le côté du haut; et treize vingt-quatrièmes de côté vis-à-vis le côté droit. Et dans le seizième
carré, il est écrit un sixième plus trois huitièmes de côté vis-à-vis le côté gauche; et un tiers plus quatre
neuvièmes sous le côté du haut.
Découper chaque carré.
Toutes les équipes devraient avoir un casse-tête avec 16 morceaux.
Interchanger les casse-têtes entre les équipes.
Le but du jeu est de refaire le casse-tête avec les bons morceaux aux bons endroits (expression = bonne réponse).
Les élèves devraient avoir du papier et un crayon pour travailler.