B2.5 Add and subtract fractions, using appropriate strategies, in various contexts.
Activity 1: Eating in Groups (Addition and Subtraction of Fractions)
Materials
- manipulatives that can help with understanding fraction operations (long strips of paper to fold, fraction strips, fraction sets, relational rods, counters)
- grid paper
Divide the class into teams of four students.
Prepare cards with food-related situations.
Each team goes to a station to solve the problem written on the card.
Manage work time and rotate when time is appropriate.
Consolidation of Learning
Ask two teams per station to send you a photo of their work.
The members of the two selected teams present their approach to solving the problem.
Emphasize process and understanding.
Question the students during the presentation.
Examples of problems on the cards
- Ginette and Marc share a chocolate bar. Ginette ate \(\frac{1}{3}\) and Marc ate half of it. What fraction of the chocolate bar is left?
- Zachary is baking four kinds of cookies for a bake sale to raise money for his Grade 8 trip. Every recipe calls for flour.
Chocolate chip cookies: \(1\frac{1}{2}\) cups
Oatmeal cookies: \(\frac{3}{4}\) cup
Sugar Cookies: \(\frac{2}{3}\) cup
Molasses Cookies: \(2\frac{1}{4}\) cups
How much flour does he need in order to make the four types of cookies?
- A group of students prepare to order 9-inch cakes for a party.
Mohammed wants \(\frac{1}{2}\) of a cake
Katrina wants \(\frac{1}{3}\) of a cake
Gigi wants \(\frac{5}{6}\) of a cake
Axel wants \(\frac{3}{4}\) of a cake
Vlad wants \(\frac{3}{8}\) of a cake
How many pizzas are needed? Will there be any left? If so, what fraction?
Activity 2: Fraction Puzzle (Addition and Subtraction)
Divide the class into teams of four students.
Each team builds an expression puzzle containing addition and subtraction on fractions.
Distribute a template (blank grid of \(4\; \times \;4\)) as below.
The students must ensure that for each common segment, they write an expression with its answer.
For example, \(\frac{3}{4}\; - \;\frac{1}{2}\; + \;\frac{1}{4}\)(expression) and \(\frac{ 1}{2}\) (answer to the expression) must be on either side of the common segment (see grid).

When completed, each team's puzzle should look like this.
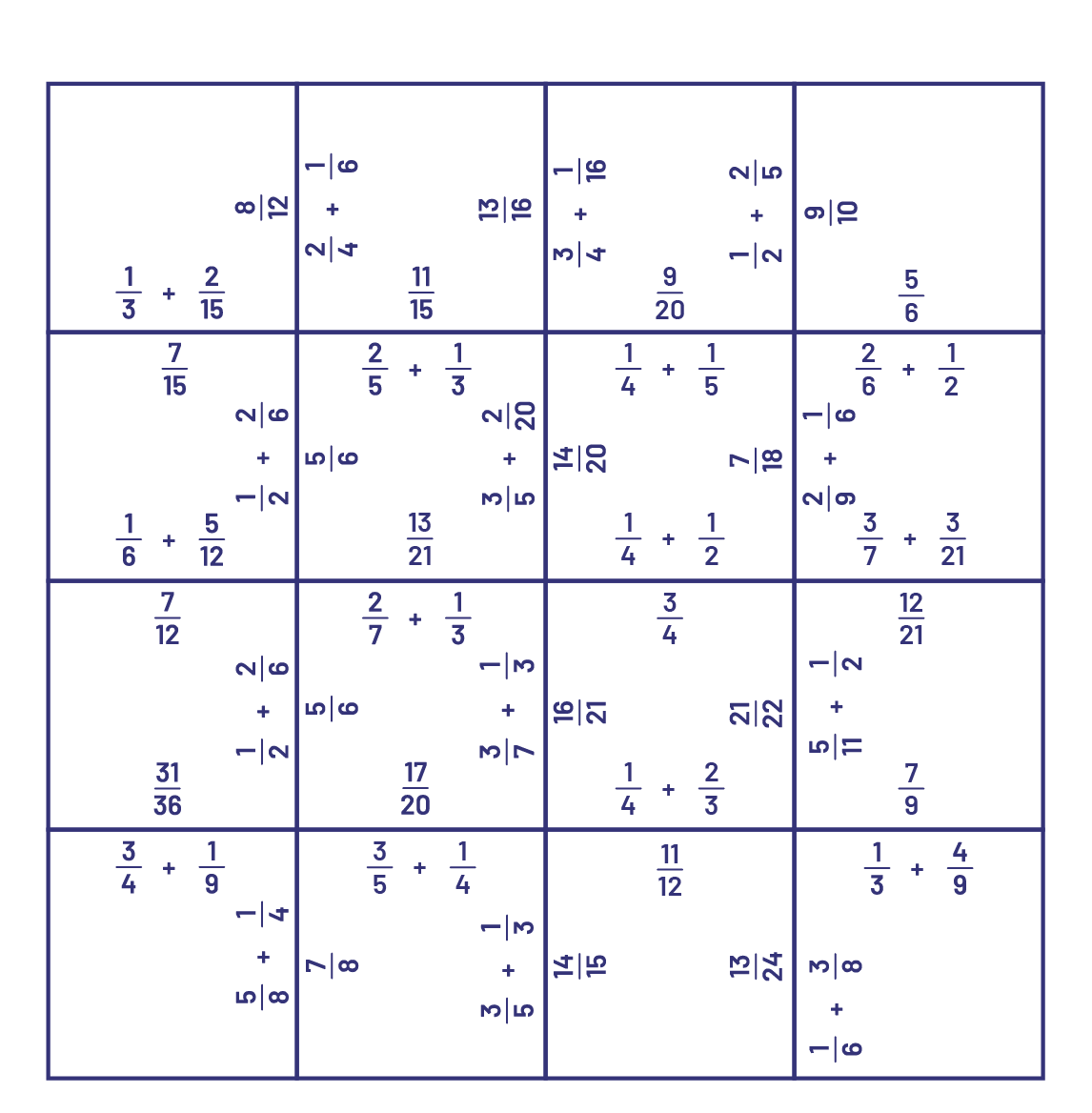
Cut out each square.
All teams should have a 16-piece puzzle.
Have teams swap their puzzles.
The goal of the game is to remake the puzzle with the right pieces in the right places (expression = right answer).
Students should have paper and pencil, grid paper and manipulatives to work with.
