B1.2 Décrire, comparer et ordonner des nombres de l’ensemble des nombres réels (rationnels et irrationnels), séparément et en les combinant, dans divers contextes.
Habileté : décrire un nombre réel
L’ensemble des nombres réels comprend l’ensemble des nombres rationnels et des nombres irrationnels.
Quantité représentée par un nombre
Comprendre la quantité, c’est développer un sens du « nombre de… » ou encore du « combien il y a de… ». Plusieurs études et sondages nationaux indiquent que les enfants, en général, ne développent pas une bonne compréhension des nombres décimaux et que plusieurs les utilisent mal et sont même incapables de résoudre des tâches dans des contextes légèrement différents. (Baroody et Coslick, 1998, p. 11-4, traduction libre)
L’apprentissage des nombres décimaux est étroitement lié à la compréhension de la notation décimale. Cette notation est employée couramment, entre autres dans le système international d’unités (SI) et dans le système monétaire. Toutefois, malgré son utilisation fréquente au quotidien et en classe, la notation décimale est loin d’être bien comprise et maîtrisée. Afin d’explorer l’apprentissage des nombres décimaux, il importe d’examiner la terminologie reliée à ces nombres et à la notation décimale.
Un nombre décimal est un nombre qui peut être exprimé en notation décimale avec une partie décimale finie (par exemple, 3,72; 12,135 64). L’ensemble des nombres décimaux inclut tous les entiers, car ces derniers peuvent être exprimés avec une partie décimale (par exemple \((-3)\; = \; (-3,0)\)). Il inclut aussi certaines fractions, comme \((- \frac{2}{5})\) et \(\frac{3}{16}\), puisque \( (- \frac{2}{5})\; = \;(- 0,4)\;\;{\rm{et}}\;\;\frac{3}{{16}}\; = \;0,187\;5\). On remarque alors que \(\frac{1}{2},\;\frac{5}{{10}}\;\;{\rm{et}}\;\;{\rm{0}}{\rm{,5}}\) sont des représentations symboliques du même nombre décimal. Il est intéressant de constater que tous les nombres décimaux peuvent être exprimés sous forme de fractions décimales, c’est-à-dire des fractions dont le dénominateur est une puissance de 10.
Exemple
\(3,72\; = \;3\frac{{72}}{{100}}\; = \;\frac{{372}}{{100}}\)
\((- 5)\; = \; (- 5,0)\; = \; (- \frac{5}{1})\)
D’autres nombres s’écrivent aussi en notation décimale, dont les nombres rationnels (partie décimale infinie et périodique) et les nombres irrationnels (partie décimale infinie et non périodique).
Or, puisque ces nombres ne sont pas composés d’une partie décimale finie, ce ne sont pas des nombres décimaux. On les regroupe plutôt, avec les nombres décimaux, sous le vocable de nombres à virgule, puisque la virgule (,) est le symbole choisi pour séparer la partie entière de la partie décimale. Dans un nombre à virgule, la partie décimale peut être finie, infinie et périodique ou infinie et non périodique. Le tableau qui suit illustre les différents types de parties décimales qui peuvent composer un nombre à virgule.
Note : En anglais, c’est le point (.) qui a été retenu pour séparer la partie entière de la partie décimale.
| Partie décimale | Explication | Exemple |
|---|---|---|
| Partie décimale finie | La partie décimale contient un nombre fini de chiffres.
Note : Les nombres dont la partie décimale est finie peuvent être représentés par des fractions décimales. |
\(0,5\;\;\;\;\left( {\frac{5}{{10}}} \right)\) \(1,458\;\;\;\;\left( {\frac{{1\;458}}{{1\;000}}} \right)\) |
|
Partie décimale infinie et périodique |
La partie décimale contient un nombre infini de chiffres dont une partie (la période) se répète
indéfiniment.
La période est indiquée par un trait horizontal placé au-dessus du chiffre ou du groupe de chiffres répété. Note : Les nombres dont la partie décimale est infinie et périodique peuvent tous être représentés par des fractions. |
\(0,353\;535 \ldots \;{\rm{ou}}\;{\;\rm{0,}}\overline {{\rm{35}}} \;\;\;\;\left( {\frac{{35}}{{99}}}
\right)\) |
| Partie décimale infinie et non périodique |
La partie décimale contient un nombre infini de chiffres, sans période. Note : Les nombres dont la partie décimale est infinie et non périodique ne peuvent pas être représentés par des fractions. |
\(\sqrt 2 \; = \;1,414\;213\;56 \ldots \) \(\pi = \;3,141\;592\;6\;5 \ldots \) |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28-29.
Pour l’ensemble des nombres rationnels, l’élève doit être en mesure de les représenter sous la forme de fractions et de nombres à virgule.
Exemples
Fraction : \((-\frac{1}{5})\; = \; (- 0,2)\)(décimal fini)
Fraction : \(\frac{1}{3}\; = \;0,333\;333 \ldots \; = \;0,\overline 3 \)
Pour l’ensemble des nombres irrationnels, l’élève devrait réaliser que ces nombres ne peuvent pas s’écrire à l’aide de la notation fractionnaire. Cependant, l’élève devra être en mesure de convertir un nombre irrationnel sous la forme décimale afin de représenter une valeur approximative de ce nombre. Rappelons que la partie décimale de tous les nombres irrationnels a un développement décimal qui est infini et non périodique.
Exemples
Valeur exacte : \(\sqrt 2 \) valeur approximative : 1,414 2
Valeur exacte : \( (- \pi) \) valeur approximative : \((- 3,141\;6)\)
Habileté : comparer et ordonner des nombres réels
Afin de comparer et ordonner tous les nombres réels (nombres rationnels et irrationnels), l’élève doit être en mesure de les convertir en nombres à virgule. Par ce fait, il doit être en mesure de reconnaître les relations entre les différentes représentations des nombres.
Relations entre des nombres exprimés sous différentes formes
Les élèves du cycle moyen et du cycle intermédiaire doivent comprendre les relations entre diverses notations d’une quantité, par exemple, les liens qui unissent des pourcentages, des nombres décimaux équivalents et des fractions équivalentes. Elles et ils doivent reconnaître qu’un nombre décimal est une fraction ou un nombre fractionnaire dont le dénominateur est un multiple de 10 (10, 100, 1 000, 10 000, etc.). Par exemple, le nombre \( (-0,5)\) est équivalent à la fraction \( (- \frac{5}{{10}})\) et le nombre 2,63 est équivalent au nombre fractionnaire \(2\frac{{63}}{{100}}\). Les élèves apprennent également qu’un pourcentage est une façon d’écrire une fraction basée sur le fractionnement d’un tout en centièmes (par exemple, 75 % est l’équivalent de \(\frac{{75}}{{100}}\)). Des modèles tels que les grilles de \(10\; \times \;10\) permettent aux élèves de visualiser les liens entre un pourcentage, la fraction correspondante et le nombre décimal correspondant.
Exemple
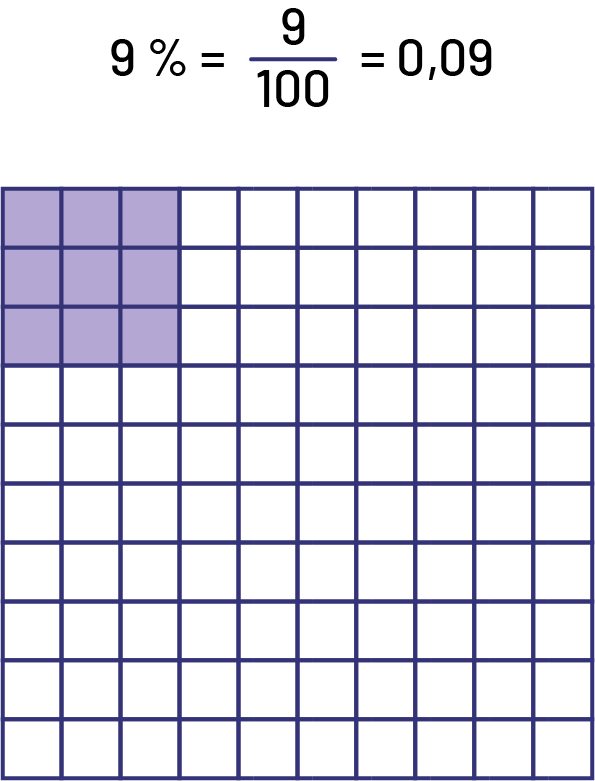 Image Dans une grille de cent unités, les neuf unités formant un carré
dans le coin supérieur gauche sont violettes tandis que le reste des unités est blanc. Au-dessus de la grille, il est
écrit : neuf pourcent égale neuf sur cent égale zéro virgule zéro neuf.
Image Dans une grille de cent unités, les neuf unités formant un carré
dans le coin supérieur gauche sont violettes tandis que le reste des unités est blanc. Au-dessus de la grille, il est
écrit : neuf pourcent égale neuf sur cent égale zéro virgule zéro neuf.
Lorsque les élèves maîtrisent bien cette relation, elles et ils sont en mesure d’identifier des fractions et des nombres décimaux équivalents aux pourcentages (par exemple \((- 25\;\%) \) est l’équivalent de \((- \frac{25}{100})\), (\(- 0,25\)) ou (\(- \frac{1}{4}\)) et de choisir la forme la plus propice au contexte. Par exemple, si une boutique offre un rabais de 20 % sur sa marchandise et qu’un polo coûte normalement 30 $, l’élève qui maîtrise la relation pourrait décider de convertir le 20 % en \(\frac{2}{{10}}\) ou\(\frac{1}{5}\) pour déterminer que 20 % de 30 $ est 6 $.
Encore une fois, il importe de mettre l’accent sur l’utilisation de modèles pour bien voir les relations entre les pourcentages, les fractions et les nombres décimaux plutôt que sur l’apprentissage formel d’une procédure pour effectuer la conversion d’une forme en une autre.
Les interventions pédagogiques doivent viser le développement, chez les élèves, d’une plus grande polyvalence avec les nombres. Pour ce faire, le personnel enseignant doit présenter des situations d’apprentissage qui mettent en jeu divers nombres et doit mettre l’accent sur les diverses façons d’écrire ces nombres, tout en faisant réfléchir sur les avantages d’une notation par rapport à une autre. Cette façon de procéder permet aux élèves de développer leur sens du nombre et leur expertise à utiliser les nombres. Il est alors souhaitable que les élèves aient l’occasion de mettre en relation des nombres présentés sous diverses formes, soit des nombres fractionnaires, des nombres décimaux, des fractions, des nombres entiers négatifs, etc.
Exemple
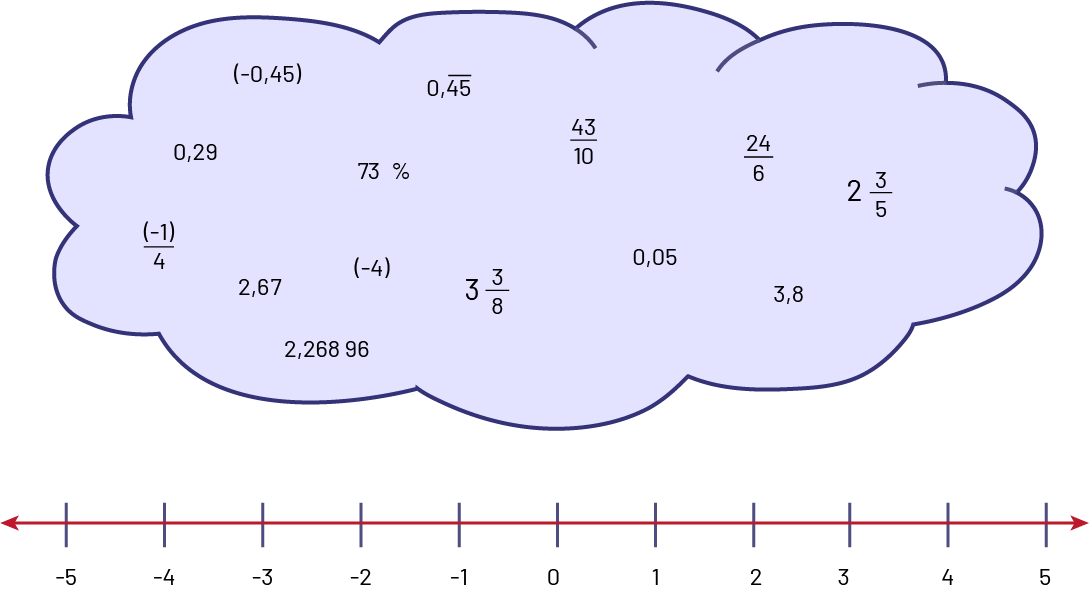
Inviter les élèves à placer divers nombres sur une droite numérique.
 Image
Au-dessus d’une double droite numérique graduée de moins cinq à cinq, il y a un nuage contenant plusieurs types de
nombres, comme des fractions, des nombres décimaux, des nombres entre parenthèses, etc.
Image
Au-dessus d’une double droite numérique graduée de moins cinq à cinq, il y a un nuage contenant plusieurs types de
nombres, comme des fractions, des nombres décimaux, des nombres entre parenthèses, etc.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 55-56.
Connaissance : nombres naturels (\(\mathbb{N}\))
L’ensemble des nombres naturels est formé des nombres entiers (0, 1, 2, 3…). Cette définition ne fait pas l’unanimité. Par exemple, dans les pays de langue anglaise, le nombre 0 est exclu des nombres naturels. On peut représenter cet ensemble de nombres par le diagramme de Venn illustré ci-contre.

Connaissance : nombres entiers (\(\mathbb{Z}\))
L’ensemble des nombres entiers est composé des nombres naturels (0, 1, 2, 3…) et des entiers négatifs \(((- 1),\; (- 2),\; (- 3),\; \ldots) \). On peut donc dire que tous les nombres naturels sont des nombres entiers, mais les nombres entiers ne sont pas tous des nombres naturels. Les élèves du cycle moyen sont exposés aux entiers négatifs dans des contextes informels (par exemple, une température de \(- 3\;^\circ {\rm{C}}\)) même si ces entiers ne font pas partie du programme-cadre de mathématiques. On peut représenter la relation entre les nombres naturels et les nombres entiers par le diagramme de Venn illustré ci-contre.

Connaissance : nombres décimaux (\(\mathbb{D}\))
L’ensemble des nombres décimaux est formé des nombres qui peuvent être exprimés sous forme décimale avec une partie décimale finie (par exemple, 3,72; \(- 5,1\); 0; \(- 7,0\); 12,135 64). Cet ensemble inclut tous les entiers, car ils peuvent être exprimés avec une partie décimale (par exemple, 3 = 3,0). Il inclut aussi certaines fractions, comme \(\frac{2}{5}\) et \(\frac{3}{{16}}\), puisque \(\frac{2}{5}\; = \;0,4\) et \(\frac{3}{16} = \;0,187\;5\). Cependant, un grand nombre de fractions sont exclues, comme \(\frac{1}{3}\;{\rm{et}}\;\frac{7}{{11}}\), car leur développement décimal nécessite un nombre infini de décimales (\(\frac{1}{3}\; = \;0,333\;33 \ldots\) et \(\frac{7}{{11}}\; = \;0,636\;363 \ldots\)). Il est intéressant de constater que tous les nombres décimaux peuvent être exprimés sous forme de fraction dont le dénominateur est une puissance de 10. (Les puissances de 10 sont 1, 10, 100, 1 000… On inclut 1 comme puissance de 10, car, par définition, \({10^0}\; = \;1\))
Exemples
\(3,72\; = \;3\frac{{72}}{{100}}\; = \;\frac{{372}}{{100}}\)
\(- 5,1 = - 5\frac{1}{{10}} \)
Puisque les nombres naturels sont tous des nombres entiers et que les nombres entiers sont tous des nombres décimaux, on peut représenter la relation entre les ensembles de nombres par le diagramme de Venn ci-contre. Note : Il n’existe pas d’ensembles de nombres à virgule. L’appellation nombre à virgule signifie simplement que l’expression du nombre contient une virgule. Ainsi, un nombre à virgule peut être un nombre décimal (par exemple, 0,45), un nombre périodique (par exemple, 0,333…) ou un nombre irrationnel (par exemple, 3,141 5…).

Connaissance : nombres rationnels (\(\mathbb{Q}\))
L’ensemble des nombres rationnels inclut tous les nombres qui peuvent être exprimés sous forme fractionnaire (\(\frac{a}{b}\)). Il inclut les nombres naturels, les nombres entiers et les nombres décimaux, ainsi que les nombres dont l’expression décimale est infinie et périodique (par exemple, \(\frac{1}{3}\; = \;0,333\;33 \ldots \; = \;0, \overline 3;\;\frac{5}{{11}}\; = \;0,454\;545 \ldots \) = \(0, \overline {45}\)). On peut représenter la relation entre les ensembles de nombres par le diagramme de Venn ci-dessous.
 Image Dans un cercle vert, on trouve la lettre Q, ainsi qu’un plus
petit cercle bleu contenant la lettre D, et lequel contient également un plus petit cercle bleu contenant la lettre Z,
lequel contient un plus petit cercle bleu contenant la lettre N.
Image Dans un cercle vert, on trouve la lettre Q, ainsi qu’un plus
petit cercle bleu contenant la lettre D, et lequel contient également un plus petit cercle bleu contenant la lettre Z,
lequel contient un plus petit cercle bleu contenant la lettre N.
Connaissance : nombres irrationnels (\(\mathbb{Q'}\))
L’ensemble des nombres irrationnels inclut tous les nombres qui ne sont pas rationnels, c’est-à-dire ceux qui ne peuvent être exprimés sous forme fractionnaire. Lorsqu’on tente d’écrire ces nombres sous forme décimale, on obtient une partie décimale infinie et non périodique, ce qui donne l’impression que ces nombres cachent toujours quelque chose, soit la suite de leurs décimales. Par exemple, on sait que le nombre \(\sqrt 2 \) existe. En effet, un carré dont les côtés ont une longueur de 1 possède des diagonales de longueur \(\sqrt 2 \).

On sait que ce nombre, multiplié par lui-même, donne 2. On sait aussi que ce nombre est à peu près égal à 1,414 2, mais qu’il est impossible de connaître toutes ses décimales et qu’il est impossible de le représenter par une fraction. Les nombres irrationnels (par exemple, \(\pi \; = \;3,141\;592\;653\;589\;793\;2 \ldots \;{\rm{et}}\;\sqrt 2 \; = \;1,414\;213\;56 \ldots \)) surviennent surtout dans des travaux mathématiques des cycles intermédiaire et supérieur. Ils ne sont pas au programme d’études du cycle moyen.
Connaissance : nombres réels (\(\mathbb{R}\))
L’ensemble des nombres réels englobe les nombres rationnels et les nombres irrationnels. Vers la fin du cycle supérieur, il devient nécessaire de résoudre certaines équations et de considérer des nombres qui vont au-delà des nombres réels.
 Image Un grand cercle vert représente les nombres réels. Il est divisé en deux parties égales par une
ligne verticale. Dans la partie de gauche, il est écrit « Q » prime. Dans la partie de droite, il est écrit « Q »
au-dessus d'un ovale bleu contenant la lettre « D », lequel contient un plus petit ovale bleu contenant la lettre « Z
», lequel contient un plus petit ovale bleu contenant la lettre « N ».
Image Un grand cercle vert représente les nombres réels. Il est divisé en deux parties égales par une
ligne verticale. Dans la partie de gauche, il est écrit « Q » prime. Dans la partie de droite, il est écrit « Q »
au-dessus d'un ovale bleu contenant la lettre « D », lequel contient un plus petit ovale bleu contenant la lettre « Z
», lequel contient un plus petit ovale bleu contenant la lettre « N ».
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 41-43.
