B1.2 Describe, compare, and order numbers in the real number system (rational and irrational numbers), separately and in combination, in various contexts.
Skill: Describing a Real Number
The set of real numbers includes the set of all rational and irrational numbers.
Quantity Represented by a Number
Understanding quantity means developing a sense of "how muchness…". Several national studies and surveys indicate that children, in general, do not develop a good understanding of decimal numbers and that many misuse them and are unable to solve tasks in slightly different contexts. (Baroody & Coslick, 1998, p. 11-4).
Learning decimal numbers is closely related to understanding decimal notation. Decimal notation is commonly used in the International System of Units (SI) and in the monetary system, among other things. However, despite its frequent use in everyday life and in the classroom, decimal notation is far from being well understood and mastered. In order to explore the learning of decimal numbers, it is important to examine the terminology related to these numbers and decimal notation.
A decimal number is a representation of a number that has a decimal point, such as 3.75. The part before the decimal point represents a whole number amount, and the part after the decimal point represents a value that is less than one. A decimal number can be expressed with terminating decimals (for example, 3.72; 12.135 64), non-terminating repeating decimals (for example, 0.33333...., 1.634634634....), and non-terminating non-repeating decimals (for example, pi (π), and square roots of non-perfect squares). Decimal numbers are a subset of real numbers.
The following table illustrates the different types of decimal parts that can compose a decimal number.
| Decimal part | Explanation | Example |
|---|---|---|
| Terminating decimal | The decimal part contains a finite number of digits.
Note: Numbers with a terminating decimal part can be represented by decimal fractions. |
\(0,5\;\left( {\frac{5}{{10}}} \right)\) \(1.458\;\left( {\frac{{1458}}{{1000}}} \right)\) |
|
Non-terminating and repeating decimals |
The decimal part contains an infinite number of digits of which a part (the period) repeats indefinitely.
The period is indicated by a dot placed above the repeated digit or group of digits. Note: Numbers with non-terminating and repeating decimal parts can all be represented by fractions. |
\(0.353\;535 \ldots \;{\rm{ou}}\;{\;\rm{0.}}\dot{3}\dot{5} \;\left( {\frac{{35}}{{99}}} \right)\) \(0.666 \ldots \;{\rm{ou}}\;{\;\rm{0.}}\dot{6} \;\left( {\frac{2}{3}} \right)\) |
| Non-terminating and non-repeating decimal |
The decimal part contains an infinite number of digits, without repeating. Note: Non-terminating and non-repeating decimal numbers can not be represented by fractions. |
\(\sqrt 2 \; = \;1.414\;213\;56 \ldots \) \(\pi = \;3.141\;592\;6\;5 \ldots \) |
Source: adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 28-29.
Students should be able to represent rational numbers as fractions and decimal numbers.
Examples
Fraction: \( - \frac{1}{5}\; = \; - 0.2\)(terminating decimal)
Fraction: \(\frac{1}{3}\; = \;0,333\;333 \ldots \; = \;0,\dot {3}\)
Student should realize that irrational numbers cannot be written using fractional notation. However, students should be able to convert an irrational number to decimal form in order to represent an approximate value of that number. Recall that the decimal part of all irrational numbers is non-terminating and non-repeating.
Examples
Exact value: \(\sqrt 2 \) approximate value: 1.414 2
Exact value: \( - \pi \) approximate value: \( - 3.141\;6\)
Skill: Comparing and Ordering Real Numbers
In order to compare and order all real numbers (rational and irrational numbers), students must be able to convert them into decimal numbers and recognize the relationships between the different representations of numbers.
Relationships Between Numbers Expressed in Different Forms
Junior and Intermediate students need to understand the relationships among various notations of a quantity, for example, the relationships among percentages, equivalent decimal numbers, and equivalent fractions. They should recognize that some decimal numbers can be represented by a fraction or a mixed number with denominators that are multiples of 10 (10, 100, 1000, 10,000, etc.). For example, the number \( (-0.5)\) is equivalent to the fraction \( (- \frac{5}{{10}})\) and the number 2.63 is equivalent to the mixed number \(2\frac{{63}}{{100}}\). Students also learn that a percent is a way of writing a fraction based on decomposing a whole into hundredths (for example, 75% is equivalent to \(\frac{{75}}{{100}}\)). Models such as 10 x 10 grids allow students to visualize the relationship between a percent, the corresponding fraction, and the corresponding decimal number.
Example
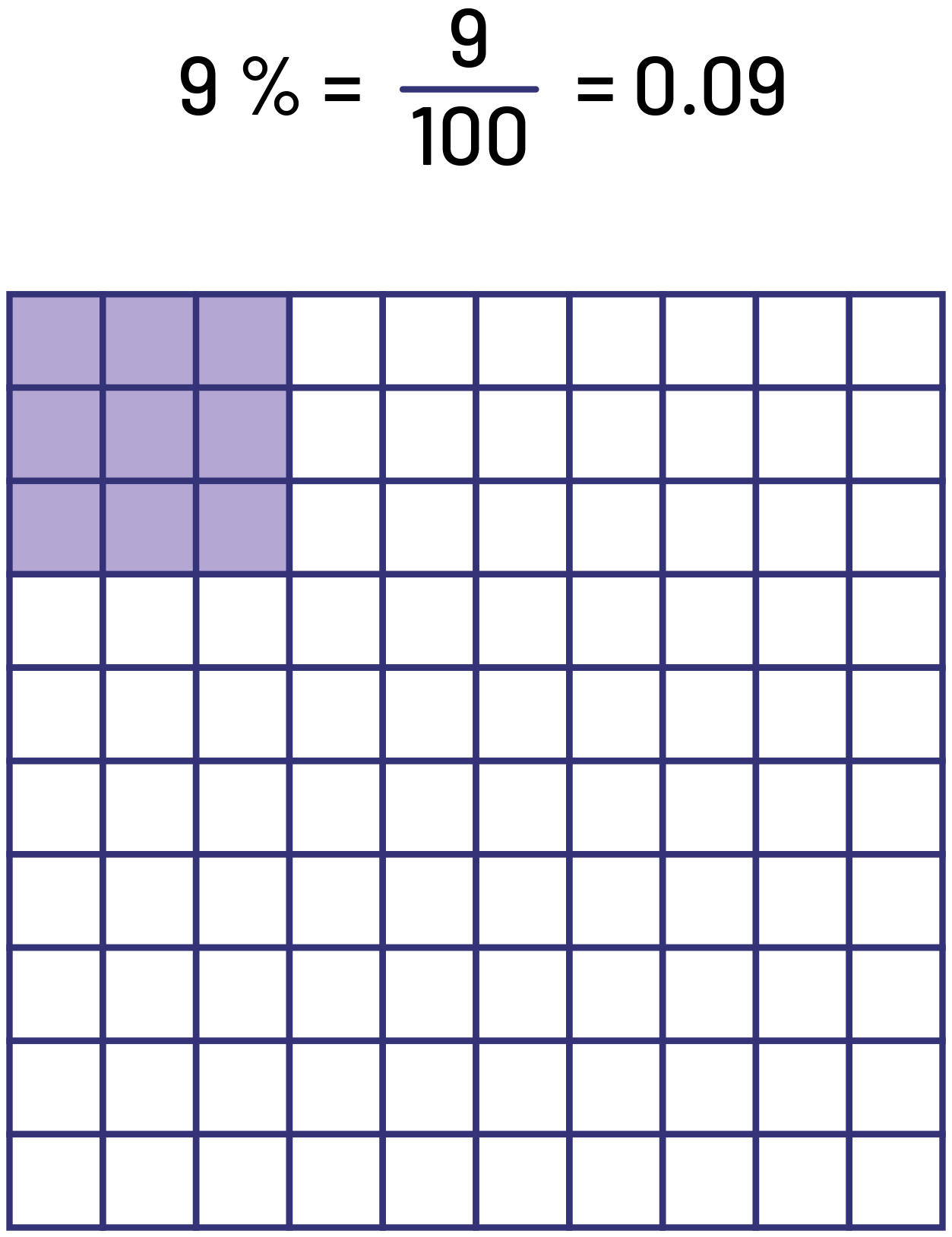
Once students have mastered this relationship, they will be able to identify fractions and decimal numbers equivalent to percents (for example, \( - 25\% \) is equivalent to \( - \frac{{25}}{{100}},\; - 0.25\;{\rm{or}}\; - \frac{1}{4}\) and choose the form best suited to the context. For example, if a store offers a 20% discount on its merchandise, and a polo shirt normally costs $30, the student who has mastered the relationship might decide to convert the 20% into \(\frac{2}{{10}}\;{\rm{ou}}\;\frac{1}{5}\) to determine that 20% of $30 is $6.
Again, it is important to emphasize the use of models to clearly see the relationships between percents, fractions, and decimal numbers rather than formally learning a procedure to perform the conversion from one form to another.
Instructional strategies should focus on developing students' versatility with numbers. To do this, teachers should present learning situations that involve a variety of numbers and emphasize the different ways of writing these numbers, while reflecting on the advantages of one notation over another. This supports students to develop their own number sense and expertise in using numbers. It is desirable that students have the opportunity to relate numbers in a variety of forms, including mixed numbers, decimal numbers, fractions, negative integers, etc.
Example
Invite students to place various numbers on a number line.
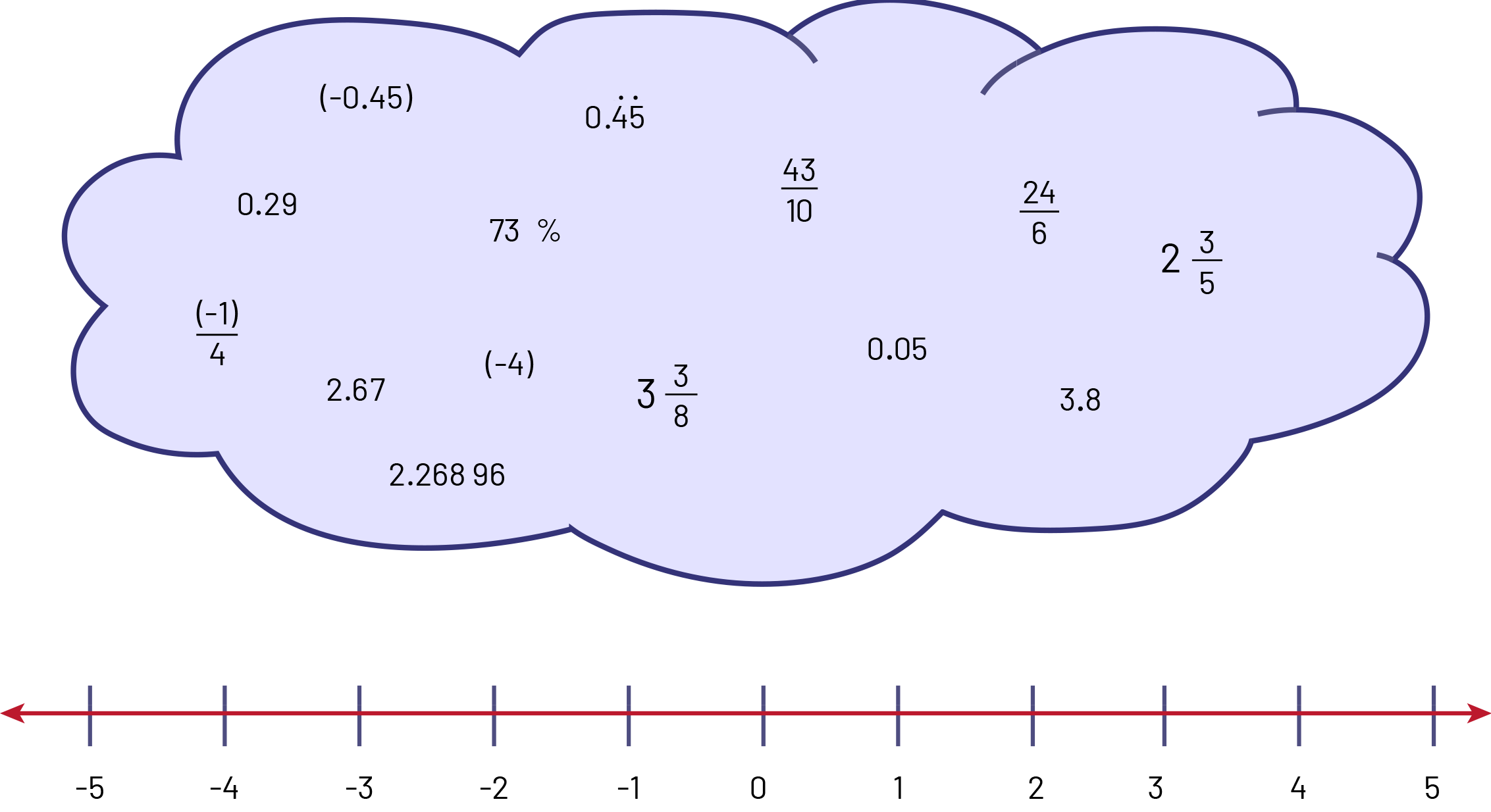
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 55-56.
Knowledge: Whole Numbers (\(\mathbb{N}\))
The set of whole numbers includes positive numbers, including zero, with no decimal or fractional parts (0, 1, 2, 3…). We can represent this set of numbers in the following circule.

Knowledge: Integers (\(\mathbb{Z}\))
The set of integers includes whole numbers (0, 1, 2, 3…) and negative integers \(((-1),\; (- 2),\; (- 3),\; \ldots) \). Thus, it can be said that all whole numbers are integers, but not all integers are whole numbers. Junior students are introduced to negative integers in informal contexts (for example, a temperature of \(- 3\;^\circ {\rm{C}}\)). The relationship between whole numbers and integers can be represented by the nested circles diagram shown below.

Knowledge: Decimal Numbers
Decimal numbers are representations of numbers with a decimal point (for example, 3.72; - 5.1; 0; - 7.0; 12.135 64). All whole numbers and integers (\(\mathbb{Z}\)), can be expressed as decimal numbers (for example, \(3\; = \;3.0\)). Fractions can also be expressed as decimal numbers that either terminate or repeat. For example, \(\frac{2}{5}\ = 0.4\) and \(\frac{3}{{16}}\; = \;0.187\;5\). However, fractions expansion requires an infinite number of decimal places, such as ( \(\frac{1}{3}\; = 0.333\;33\)) and \(\frac{7}{{11}}\; = \;0.636\;363\)…Interestingly, all fractions with a denominator that is a power of 10 can be expressed as a decimal number. For example:
\(3.72\; = \;3\;\frac{{72}}{{100}}\; = \;\frac{{372}}{{100}}\)
\( - 5.1\; = \;- 5\;\frac{1}{10} = \;\frac{-51}{10}\)
\(5\; = \;5.0\; = \;\frac{5}{1}\)
Since all whole numbers are integers and all integers can be expressed as decimal numbers, we can represent the relationship between the numbers by the diagram below.

There is no set of decimal numbers. A decimal number is an expression of a number with a decimal point.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 42.
The decimal point plays a significant role in decimal notation. It separates the whole part from the decimal part.

The position of the ones defines the whole according to which are formed on the one hand the tenths, the hundredths and the thousandths and on the other hand the tens, the hundreds and the thousands.It can therefore be said that the ones, identified by the decimal point, is at the heart of the decimal system.

This recognition of the role of the units digit is evidenced by the prefixes given to the place values of the digits on either side of the unit. Thus, tenths represent a quantity ten times smaller than the unit.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 51.
Knowledge: Rational Numbers (\(\mathbb{Q}\))
The set of rational numbers includes all numbers that can be expressed in fractional form. It includes whole numbers and integers. We can represent the relation between the whole numbers, integers, decimal numbers, and rational numbers by the nested circles diagram below.

Knowledge: Irrational Numbers (\(\mathbb{Q'}\))
The set of irrational numbers includes all numbers that are not rational, that is, those that cannot be expressed in fractional form. When we try to write these numbers in decimal form, we obtain a non-terminating and non-repeating decimal part, which gives the impression that these numbers always hide something, namely the sequence of their decimals. For example, we know from the following situation that the number \(\sqrt 2 \) exists. A square whose sides have a length of 1 has diagonals of length \(\sqrt 2 \).
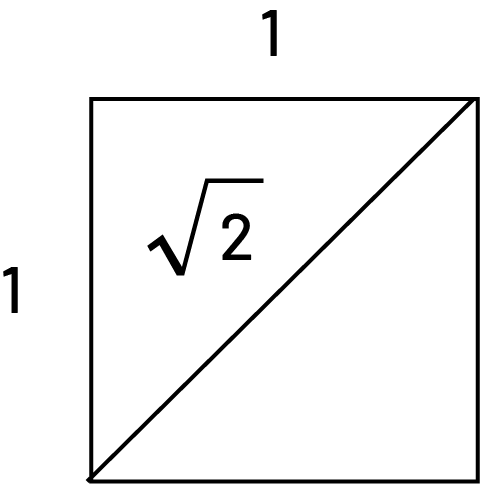
We know that this number, multiplied by itself, gives 2. We also know that this number is approximately equal to 1.414 2, but that it's impossible to know all its decimals and that it's impossible to represent it by a fraction. Irrational numbers (for example, \(\pi \; = \;3.141\;592\;653\;589\;793\;2 \ldots \;{\rm{and}}\;\sqrt 2 \; = \;1.414\;213\;56 \ldots \)) occur mainly in intermediate and senior mathematical work.
Knowledge: Real Numbers (\(\mathbb{R}\))
The set of real numbers includes both rational and irrational numbers. This set of numbers has been the focus of learning in the Elementary Curriculum.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 41-43.
