B1.3 Estimer et calculer des racines carrées, dans divers contextes.
Habileté : estimer des racines carrées
Les carrés parfaits peuvent être calculés. Les carrés imparfaits ne peuvent qu’être estimés.
Toutes les racines carrées qui ne sont pas des racines de carrés parfaits sont des nombres irrationnels.
Les racines carrées des carrés non parfaits sont irrationnelles et laissées sous forme radicale (par exemple, \(\sqrt 3 \)) ou une approximation exprimée à l’aide d’un nombre décimal.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Estimer à l’aide des carrés parfaits
Les élèves doivent connaître les carrés parfaits les plus communs tels que 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 225 et 400 ainsi que leurs racines carrées. Les carrés parfaits deviennent ainsi des repères afin d’estimer la valeur d’une racine carrée.
Afin d’estimer \(\sqrt {30}\), l’élève devrait être en mesure de déduire que \(\sqrt {30} \) se situe entre \(\sqrt {25} \) et celle de \(\sqrt {36} \) Donc, l’élève sait que la réponse recherchée se situe entre 5 et 6 et puisque le radicande 30 est presque au milieu (entre 25 et 36), la racine carrée approximative sera 5,5.
Habileté : calculer des racines carrées
Seuls les carrés parfaits peuvent être calculés. Les carrés et les racines carrées étant des opérations inverses, la connaissance des faits de multiplication de base sert à calculer les racines de carrés parfaits. Par exemple, sachant que \(9\; \times \;9\) fait 81, l’élève sait donc que la racine carrée de 81 est 9. L’utilisation de matériel à base dix ou du modèle de la disposition rectangulaire peut faciliter le calcul de racines carrées au-delà de 144.
Exemple
Pour trouver \(\sqrt {169} \), l’élève dispose le matériel à base dix afin de représenter un carré ou se sert de la disposition rectangulaire symbolique afin de déterminer la longueur de chaque côté.
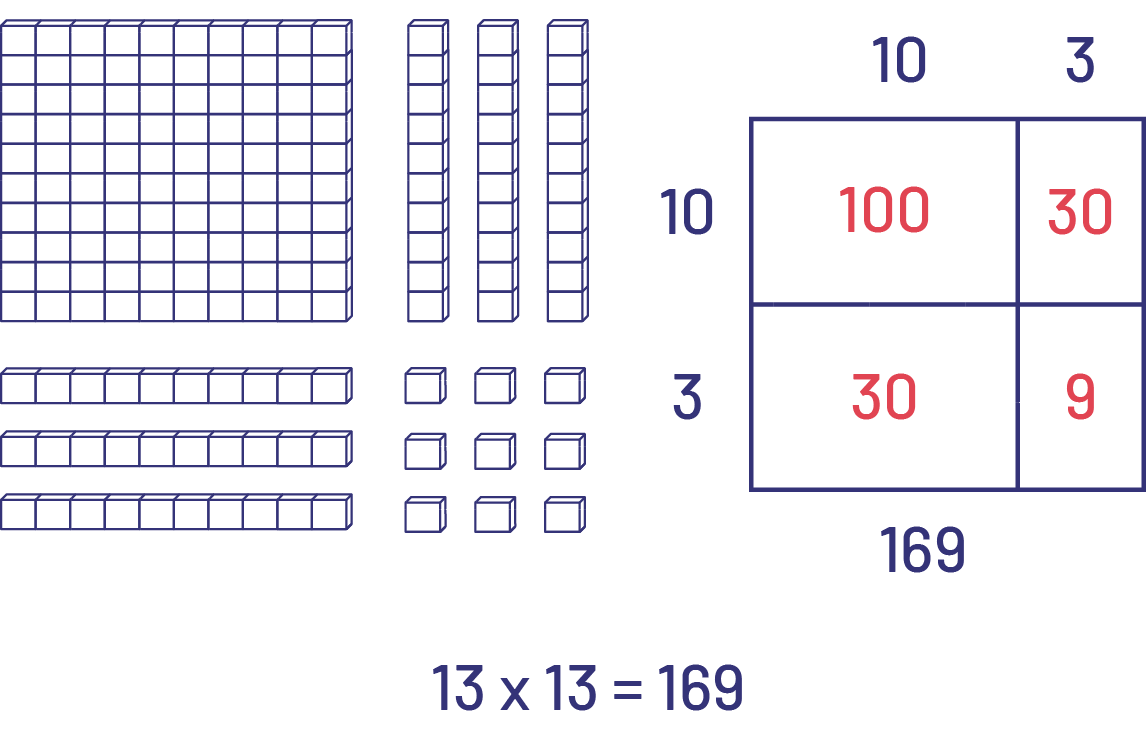Image La multiplication treize fois treize égale 169 est représentée par des cubes unités ainsi que par un
rectangle
Les cubes unités se présentent sous la forme d’une grille de cent unités, d’un ensemble de trois bâtonnets
verticaux de dix unités, d’un ensemble de trois bâtonnets horizontaux de dix unités et de neuf unités individuelles.
Le rectangle est divisé en quatre parties. De gauche à droite et de haut en bas : la première partie présente le
nombre cent, la deuxième partie présente le nombre trente, la troisième partie présente le nombre cent et la
quatrième partie présente le chiffre neuf. Les côtés horizontaux présentent respectivement un dix et un trois tandis
que les côtés verticaux présentent respectivement un dix et un trois.
Connaissance : racine carrée
Nombre qui, lorsqu’il est multiplié par lui-même, donne le nombre (le carré). Par exemple, 3 est la racine carrée de 9, car \(3\; \times \;3\; = \;9\).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
La racine carrée d’un nombre rationnel positif est toujours positive. La racine carrée d’un nombre rationnel négatif n’existe pas dans les nombres réels.
Connaissance : carré parfait
Nombre qui peut être exprimé comme le produit de deux nombres naturels identiques. Par exemple, \(9 = \;3\; \times \;3\;\); ce qui signifie que 9 est un carré parfait.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : ensemble de nombres irrationnels (\(\mathbb{Q'}\))
L’ensemble des nombres irrationnels inclut tous les nombres qui ne sont pas rationnels, c’est-à-dire ceux qui ne peuvent être exprimés sous forme fractionnaire. Lorsqu’on tente d’écrire ces nombres sous forme décimale, on obtient une partie décimale infinie et non périodique, ce qui donne l’impression que ces nombres cachent toujours quelque chose, soit la suite de leurs décimales. Par exemple, on sait que le nombre \(\sqrt 2 \) existe. En effet, un carré dont les côtés ont une longueur de 1 possède des diagonales de longueur \(\sqrt 2 \).
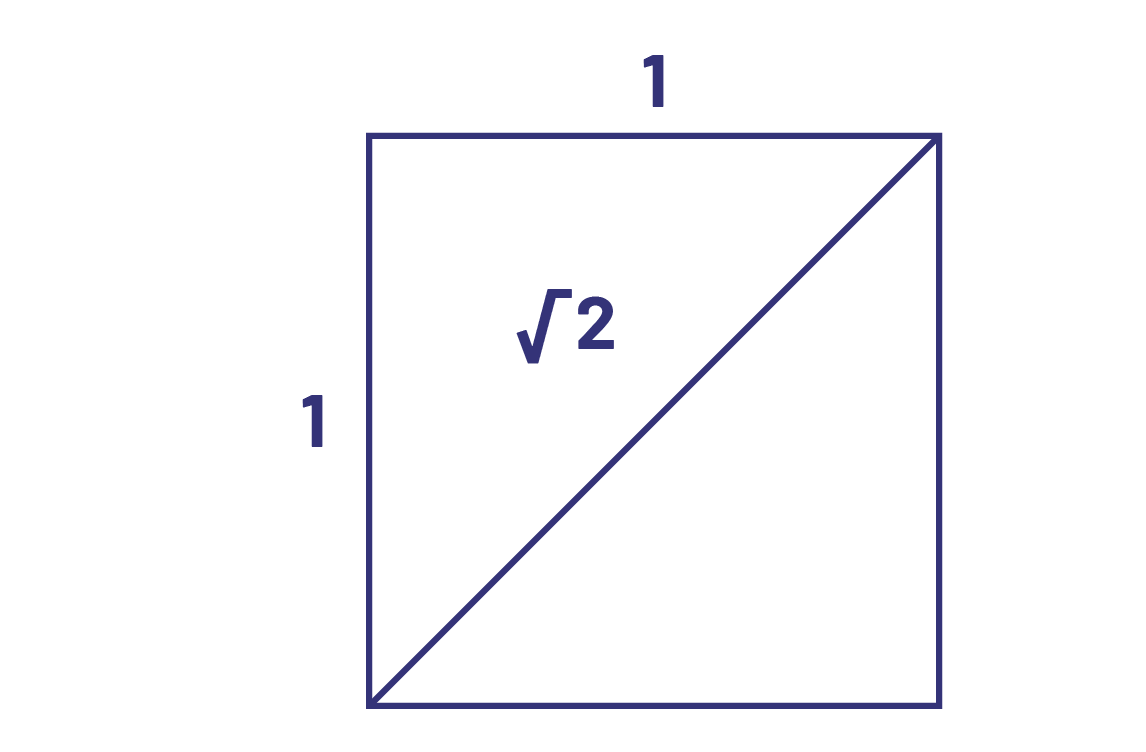
On sait que ce nombre, multiplié par lui-même, donne 2. On sait aussi que ce nombre est à peu près égal à 1,414 2, mais qu’il est impossible de connaître toutes ses décimales et qu’il est impossible de le représenter par une fraction. Les nombres irrationnels (par exemple, \(\pi \; = \;3,141\;592\;653\;589\;793\;2 \ldots \;{\rm{et}}\;\sqrt 2 \; = \;1,414\;213\;56 \ldots \)) surviennent surtout dans des travaux mathématiques des cycles intermédiaire et supérieur. Ils ne sont pas au programme d’études du cycle moyen.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 43.