B1.3 Estimate and calculate square roots, in various contexts.
Skill: Estimating Square Roots
Perfect squares can be calculated. Imperfect squares can only be estimated.
The square roots of non-perfect squares are irrational and left in radical form (for example, \(\sqrt 3 \)) or approximated to a decimal number.
Source: The Ontario Curriculum. Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.
Estimating With Perfect Squares
Students should know the most common perfect squares such as 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 225, and 400 and their square roots. The perfect squares thus become benchmarks for estimating the value of a square root.
In order to estimate \(\sqrt {30}\), students should be able to deduce that \(\sqrt {30} \) lies between \(\sqrt {25} \) and that of \( \sqrt {36} \) So the student knows that the answer they are looking for is between 5 and 6 and since the radicand 30 is almost in the middle (between 25 and 36), the approximate square root will be 5.5.
Skill: Calculating Square Roots
Only perfect squares can be calculated. Since squares and square roots are inverse operations, knowledge of basic multiplication facts is used to calculate the roots of perfect squares. For example, knowing that \(9; \times \;9\) is 81, the student therefore knows that the square root of 81 is 9. Using base ten materials or the array model can make it easier to calculate square roots beyond 144.
Example
To find \(\sqrt {169} \), students arrange base ten materials to represent a square or use the array model to determine the length of each side.
Knowledge: Square Root
A number that, when multiplied by itself, equals the number. For example, 3 is the square root of 9, because \(3 \times 3 = 9 \).
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
The square root of a positive rational number is always positive. The square root of a negative rational number does not exist in real numbers.
Knowledge: Perfect Square
A number that can be expressed as the product of two identical natural numbers. For example, 9 = 3 × 3; thus 9 is a perfect square.
Source : The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020..
Knowledge : Set of Irrational Numbers (\(\mathbb{Q'}\))
The set of irrational numbers includes all numbers that are not rational, that is, those that cannot be expressed in fractional form. When we try to write these numbers in decimal form, we obtain a non-terminating and non-repeating decimal part, which gives the impression that these numbers always hide something, namely the sequence of their decimals. For example, we know that the number \(\sqrt 2 \) exists. Indeed, a square whose sides have a length of 1 has diagonals of length \(\sqrt 2 \).
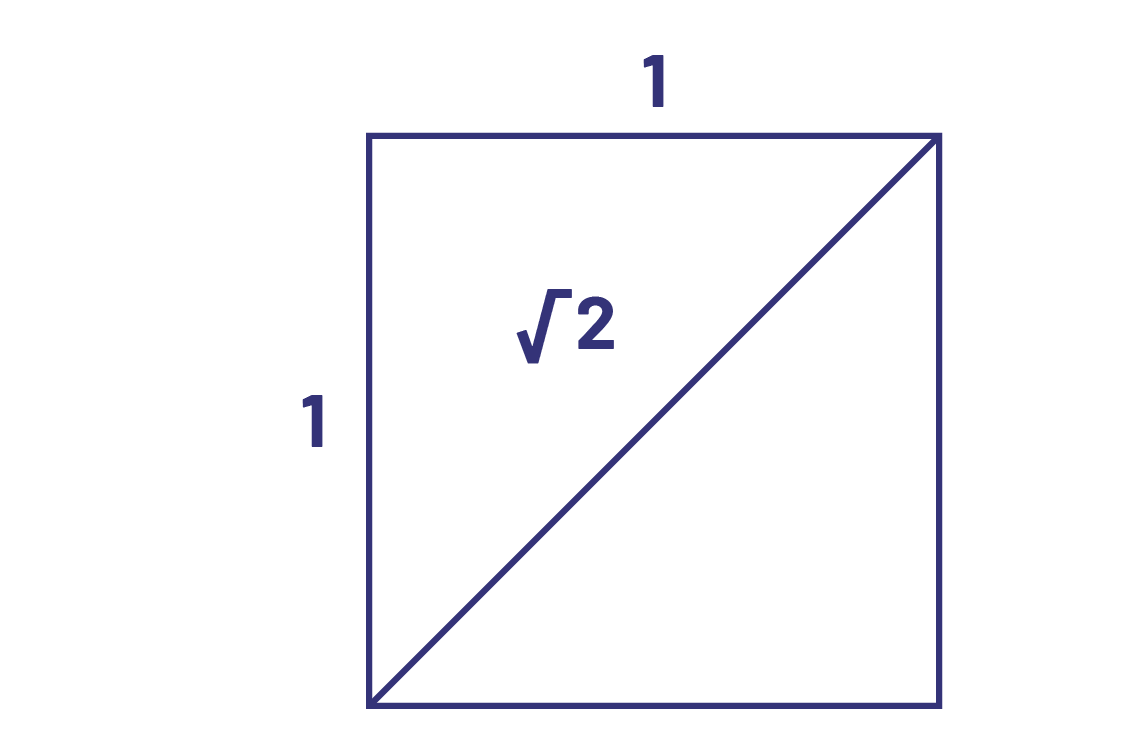
We know that this number, multiplied by itself, gives 2. We also know that this number is approximately equal to 1.414 2, but that it's impossible to know all its decimals and that it's impossible to represent it by a fraction. Irrational numbers (for example, \(\pi \; = \;3,141\;592\;653\;589\;793\;2 \ldots \;{\rm{et}}\;\sqrt 2 \; = \;1,414\;213\;56 \ldots \)) occur mainly in intermediate and senior mathematical work. They are not part of the junior division curriculum.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 43.