B1.4 Utiliser les fractions, les nombres décimaux et les pourcentages, y compris des pourcentages de plus de 100 % et de moins de 1 %, de manière interchangeable et avec souplesse pour résoudre divers problèmes.
Habileté : décrire les relations et représenter les équivalences entre des fractions, des nombres décimaux jusqu’aux millièmes et des pourcentages, à l’aide d’outils et de schémas appropriés, dans divers contextes
Pour bien développer le sens du nombre, il est important que les élèves se forment des images des quantités représentées par les nombres. Dans le cas des nombres décimaux, les lire correctement permet de s’en faire une meilleure représentation mentale et de faire appel à leurs connaissances des fractions (par exemple, 0,75 se lit « soixante-quinze centièmes » et non pas « zéro virgule soixante-quinze »). Il faut inciter les élèves à utiliser plusieurs modèles pour favoriser la création de diverses représentations mentales et ainsi pour décrire les relations entre les fractions et les nombres décimaux.
Exemple
Image Le premier nombre est un dixième ou zéro virgule un. Il est
représenté par une rangée de dix unités, l’une est rouge et les neuf autres sont vertes. Le deuxième nombre est 75 sur
100 ou zéro virgule 75. Il est représenté par une grille de 100 unités; 75 sont rouges et 25 sont blanches.
Lors de la représentation de nombres décimaux à l’aide de modèles, il y a une adaptation à faire, car ces mêmes modèles étaient utilisés jusqu’alors pour représenter d’autres concepts (par exemple, la languette représentait une dizaine de cubes). Les élèves doivent comprendre que l’unité a changé. Dans le premier des deux exemples précédents, c’est l’objet au complet qui représente l’unité (le tout); dans le deuxième, c’est le grand carré au complet qui représente l’unité (le tout).
Les élèves doivent aussi se former une représentation mentale de nombres décimaux supérieurs à un. À la lecture d’un tel nombre décimal, elles et ils doivent se représenter mentalement la quantité qu’il représente en interprétant les deux parties qui le composent : la partie entière et la partie décimale. Par exemple, elles et ils doivent reconnaître que le nombre 8,24 représente 8 entiers et une partie d’un autre entier identique. Elles et ils peuvent alors visualiser une quantité entre 8 et 9.
Exemple
Avec le temps, les élèves sont en mesure de se représenter mentalement la quantité en tenant compte du contexte. Par exemple, dans une situation où il est question d’un article qui coûte 197,98 $, l’élève qui reconnaît que 197,98 $ représente un peu plus que 197 $ peut ensuite visualiser ou concevoir que, dans ce contexte, le montant de 197,98 $ peut être représenté approximativement par 10 billets de 20 $.
Les élèves doivent être capables de se créer une représentation mentale d’un pourcentage, comme elles et ils le font pour les nombres décimaux. La nature même du pourcentage leur permet de visualiser plus facilement une quantité, car il s’agit toujours d’un rapport avec 100. Il faut aussi bien comprendre qu’un pourcentage est une autre façon de représenter une quantité.
Exemple
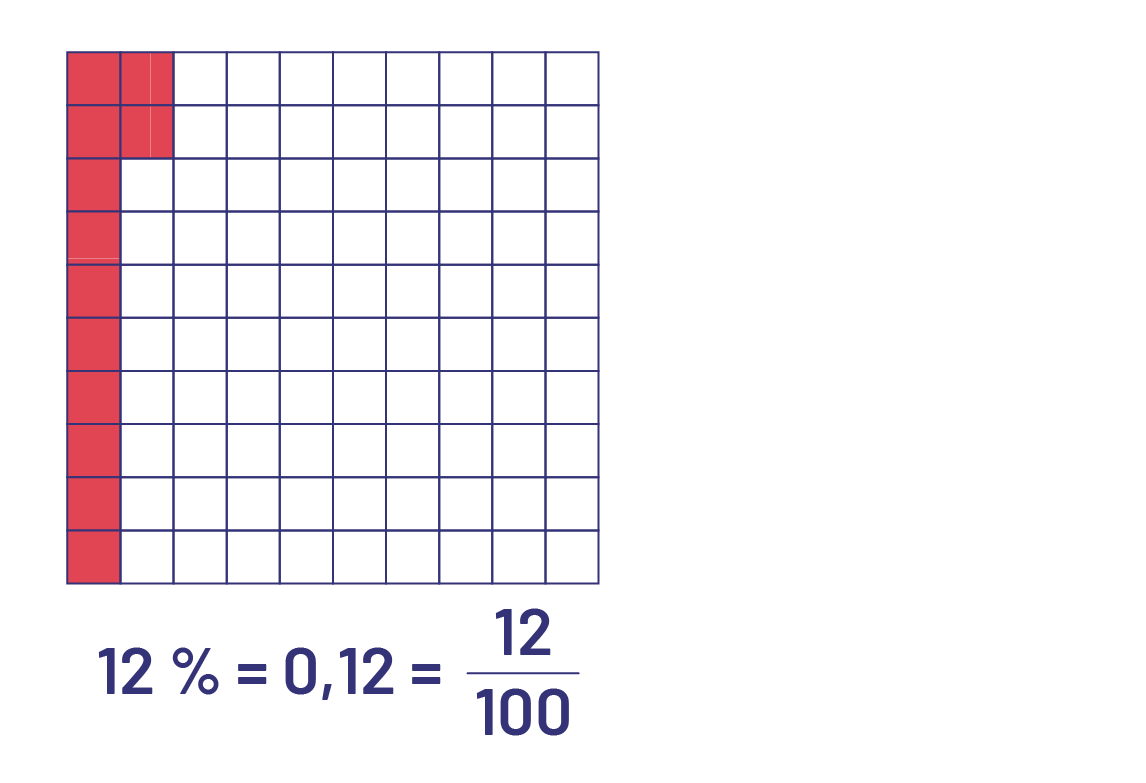
Il est important de reconnaître l’égalité entre les diverses représentations des nombres ou des expressions numériques. Dans le cadre des nombres décimaux, les élèves doivent reconnaître l’égalité entre un nombre décimal, la fraction décimale correspondante et le pourcentage.
Les élèves doivent comprendre que puisque la notation décimale n’est qu’une autre façon de représenter une fraction décimale, il est alors possible d’établir une relation d’égalité entre les deux notations (par exemple, 0,3 = \(\frac{3}{10}\)). En reconnaissant cette égalité, elles et ils sont en mesure d’associer une valeur de position à chacune des décimales qui composent un nombre décimal, soit successivement les dixièmes, les centièmes, les millièmes et ainsi de suite.
Exemple
Image Trois équations sont présentées.Première équation : trois sur dix égale zéro virgule trois.
En dessous, le mot
« dixièmes » pointe avec des flèches vers le dénominateur et vers le trois de zéro virgule trois.Deuxième équation :
sept sur cent égale zéro virgule zéro sept. En dessous, le mot « centièmes » pointe avec des
flèches vers le dénominateur et vers le sept de zéro virgule zéro sept.Troisième équation : cinq sur mille égale zéro
virgule zéro zéro cinq. En dessous, le mot « millièmes » pointe avec
des flèches vers le dénominateur et vers le cinq de zéro virgule zéro zéro cinq.
Les élèves qui n’ont pas compris cette association sont parfois portés à représenter une fraction telle que \(\frac{2}{5}\) par 0,2 ou 0,25. La description ci-après décrit des comportements observables d’élèves ayant acquis une compréhension conceptuelle des nombres et du lien entre leurs différentes représentations.
Compréhension conceptuelle des nombres
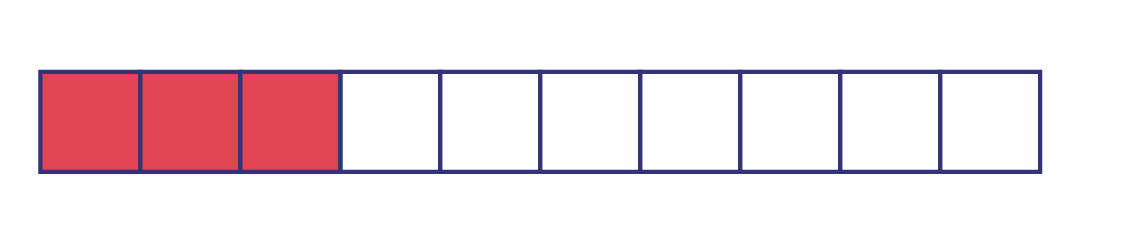
Nombre : 0,3
Comportements observables :
- L’élève peut en faire la lecture (trois dixièmes).
- L’élève peut écrire le nombre en notation fractionnaire, soit \(\frac{3}{{10}}\).
- L’élève peut représenter le nombre à l’aide de matériel concret ou semi-concret.
Exemple
Nombre : \(\frac{{16}}{{100}}\)
Comportements observables :
- L’élève peut en faire la lecture (seize centièmes).
- L’élève peut écrire le nombre en notation décimale, soit 0,16.
- L’élève peut représenter le nombre à l’aide de matériel concret ou semi-concret.
Exemple
Nombre : \(\frac{2}{7}\)
Comportements observables :
- L’élève peut en faire la lecture (deux septièmes).
- L’élève sait que la fraction \(\frac{2}{7}\) n’est pas représentée par 0,2 puisqu’elle ou il sait que \(0,2\; = \;\frac{2}{{10}}\).
Pour établir la relation d’égalité entre une fraction dont le dénominateur n’est pas une puissance de dix (par exemple, \(\frac{1}{4}\)) et le nombre décimal correspondant, il est nécessaire de recourir au concept de fractions équivalentes. Par exemple, les élèves peuvent utiliser des bandes d’égales longueurs telles qu’illustrées ci-dessous pour constater que \(\frac{1}{4}\) se situe entre \(\frac{2}{{10}}\) et \(\frac{3}{{10}}\).
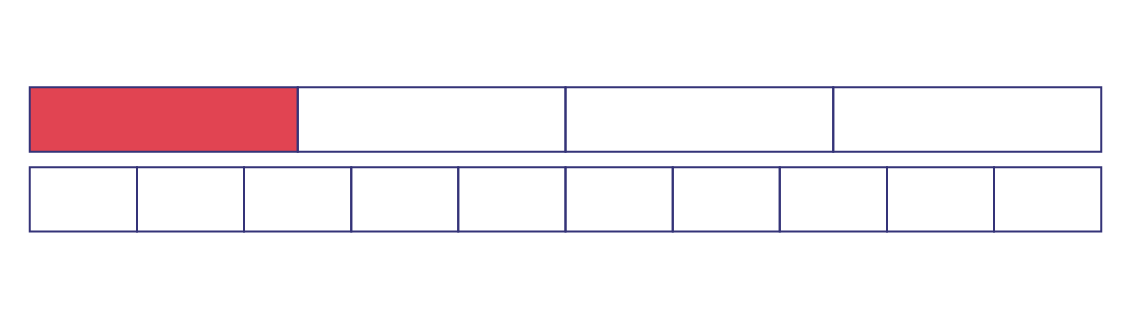Image
Deux longs rectangles minces de longueur égale sont placés l’un sous l’autre en étant vis-à-vis. Le premier rectangle
est divisé en quatre parties égales. La première partie est rouge tandis que les trois autres sont blanches. Le
deuxième rectangle est divisé en dix parties égales, toutes blanches.
Elles et ils peuvent ensuite subdiviser les dixièmes en dix parties égales, créant ainsi cent parties égales, soit des centièmes du tout et reconnaître que \(\frac{{25}}{{100}}\) est une fraction équivalente à \(\frac{1}{4}\).
Image
Deux longs rectangles minces de longueur égale sont placés l’un sous l’autre en étant vis-à-vis. Le premier rectangle
est divisé en quatre parties égales. La première partie est rouge tandis que les trois autres sont blanches. Le
deuxième rectangle est divisé en cent parties égales. Des lignes plus foncées séparent les groupes de dix. Une ligne
rouge se trace à la vingt-cinquième part, vis-à-vis la fin de la partie rouge du rectangle du haut.
Puisque \(\frac{{25}}{{100}}\; = \;0,25\), elles et ils peuvent conclure que la fraction \(\frac{1}{4}\) peut aussi être représentée en notation décimale par 0,25 (\(\frac{1}{4}\; = \;\frac{{25}}{{100}}\; = \;0,25\)).
Ce genre d’exemple permet aux élèves de reconnaître que toutes les fractions qui peuvent être exprimées par une fraction décimale équivalente peuvent être représentées par un nombre décimal. C’est le cas notamment des fractions exprimées en demis, en quarts, en cinquièmes et en vingtièmes comme le démontre le tableau suivant.
| Fraction | Fraction décimale équivalente | Nombre décimal |
|---|---|---|
| \(\frac{1}{2}\) | \(\frac{5}{{10}}\) | 0,5 |
| \(\frac{3}{4}\) | \(\frac{{75}}{{100}}\) | 0,75 |
| \(\frac{2}{5}\) | \(\frac{4}{{10}}\) | 0,4 |
| \(\frac{7}{{20}}\) | \(\frac{{35}}{{100}}\) | 0,35 |
Note : Certaines fractions (par exemple, \(\frac{2}{3}\), \(\frac{3}{7}\), \(\frac{5}{{11}}\)) ne peuvent être représentées par une fraction décimale équivalente. Ces fractions ne sont donc pas des nombres décimaux. Elles peuvent cependant être exprimées par des nombres à virgule ayant une partie décimale périodique (par exemple, \(\frac{2}{3}\; = \;0, \overline 6\); \(\frac{3}{7}\; = \;0,\overline{428\;571}\); \(\frac{5}{{11}}\; = \;0,\overline{45}\)) en divisant le numérateur par le dénominateur.
On sait qu’un nombre décimal représente une fraction dont le dénominateur est une puissance de 10 (par exemple, \(0,3\; = \;\frac{3}{{10}}\); \(0,47\; = \;\frac{{47}}{{100}}\)). Le concept de pourcentage étant intimement lié au concept de fraction, il n’y a qu’un pas à faire pour relier le pourcentage, le nombre décimal et la fraction décimale. À la fin du cycle moyen, les élèves qui ont acquis un bon sens du nombre peuvent passer d’une notation à une autre sans difficulté.
Exemple
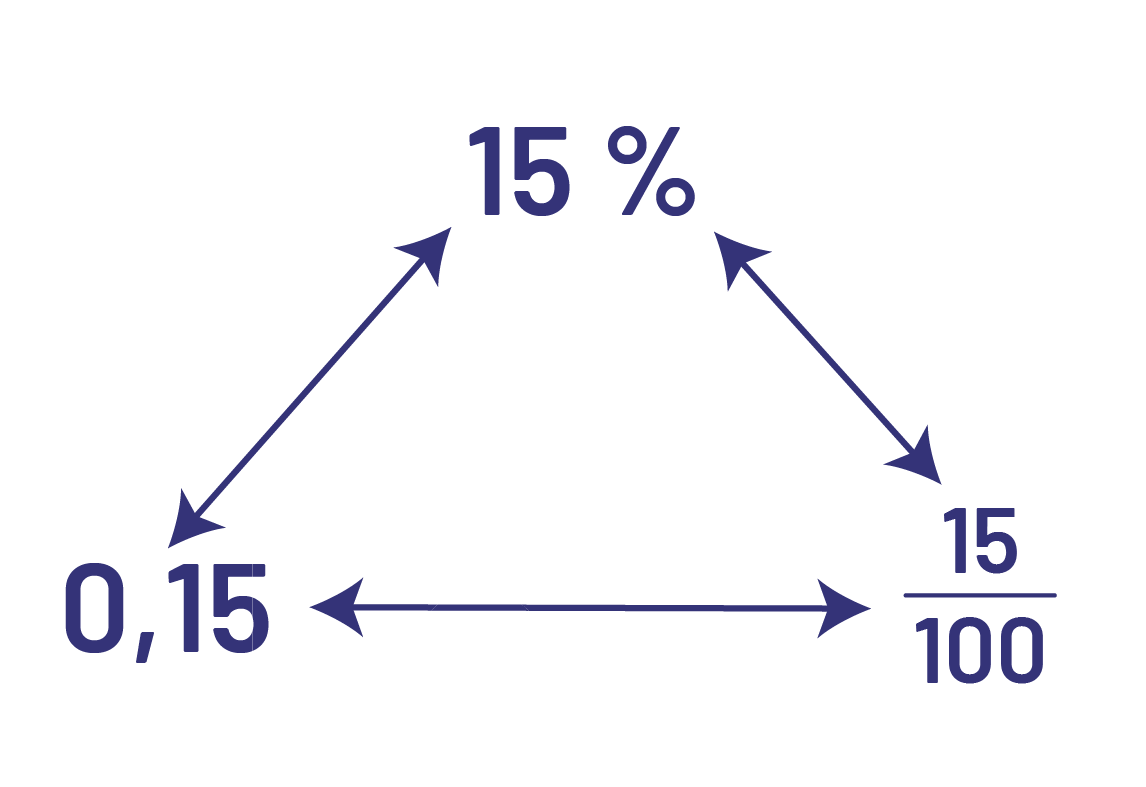Image Nombres disposés en forme de triangle. En haut, 15 pourcent, en
bas à gauche, zéro virgule 15, et en bas à droite, 15 sur cent. Ils sont tous reliés entre eux par des flèches à
double sens.
Pour aider les élèves à développer cette habileté, il faut régulièrement les inviter à exprimer leurs réponses en utilisant une autre notation. Par exemple, le personnel enseignant peut inciter l’élève qui a répondu que \(\frac{3}{4}\) des jeunes de la classe ont les cheveux noirs à exprimer aussi cette réponse en notation décimale (0,75) et en pourcentage (75 %).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 46-51.
Certains nombres décimaux, lorsqu’ils sont convertis en pourcentage, donnent un pourcentage entier ou un pourcentage avec une partie décimale (par exemple, 0,15 = 15 %; 0,642 = 64,2 %; 3,425 = 342,5 %).
Les pourcentages peuvent être des nombres naturels (par exemple, 32 %, 168 %) ou des nombres décimaux (par exemple, 0,5 %; 43,6 %; 108,75 %).
Il existe trois types de situations où interviennent des pourcentages : déterminer le pourcentage qu’une quantité représente par rapport à un tout; trouver le pourcentage d’un nombre; et trouver un nombre alors que le pourcentage qu’il représente est donné.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Les élèves croient souvent, à tort, qu’un pourcentage ne peut dépasser 100 (100 %). Or, certaines situations de la vie courante mènent à des pourcentages supérieurs à 100 %. Pour bien comprendre, ces situations peuvent être explorées au moyen de représentations concrètes ou semi-concrètes où les quantités sont mises en relation avec le tout. On peut aussi utiliser la notation fractionnaire ou décimale.
Exemple
À la suite d’une augmentation de 25 %, on peut affirmer que la nouvelle quantité représente 125 % de la quantité initiale.
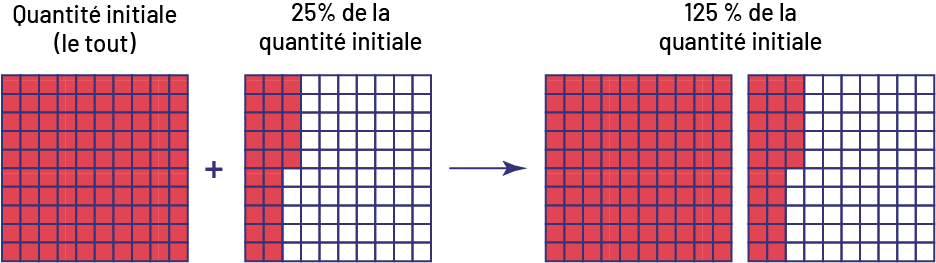Image Quatre grilles de cent unités sont présentées côte à côte. La
première grille possède 100 unités rouges. Au-dessus, il est écrit : Quantité initiale, le tout. Entre la première et
la deuxième grille, il y a un symbole plus. La deuxième grille possède 25 unités rouges et 75 unités blanches.
Au-dessus, il est écrit : 25 pourcent de la quantité initiale. Elle se lie à la troisième grille par une flèche. La
troisième grille est identique à la première, et la quatrième grille est identique à la deuxième. Au-dessus des deux
dernières grilles, il est écrit : 125 pourcent de la quantité initiale.
Ainsi, la nouvelle quantité représente \(\frac{{125}}{{100}}\) (cent vingt-cinq centièmes) de la quantité initiale ou 125 % de la quantité initiale. Cependant, une augmentation de 125 % signifie que 125 % du tout est ajouté à la quantité initiale. La nouvelle quantité représente alors \(\frac{{225}}{{100}}\) (deux cent vingt-cinq centièmes) de la quantité initiale ou 225 % de la quantité initiale.
Image
Six grilles de cent unités sont présentées côte à côte. La première grille possède 100 unités rouges. Au-dessus, il
est écrit : Quantité initiale, le tout. Entre la première et la deuxième grille, il y a un symbole plus. La deuxième
grille possède 100 unités rouges tandis que la troisième possède 25 unités rouges. Au-dessus des deuxième et troisième
grilles, il est écrit : 125 pourcent de la quantité initiale. La troisième grille se lie à la quatrième par une
flèche. La quatrième et la cinquième grilles possèdent 100 unités rouges, et la sixième possède 25 unités rouges.
Au-dessus de ces trois dernières, il est écrit : 225 pourcent de la quantité initiale.
Connaissance : pourcentage
Le pourcentage est une façon particulière de présenter une fraction. Il est souvent employé dans la vie courante. Une expression numérique comme 30 % (qui se lit « trente pour cent ») est en réalité une autre notation du nombre trente centièmes, soit \(\frac{{30}}{{100}}\) ou 0,30. Afin de faciliter la compréhension du concept de pourcentage, il faut d’abord amener les élèves à établir le lien entre le pourcentage et la fraction dont le dénominateur est 100, et ce, à l’aide de matériel concret ou semi-concret.
Exemple
Les élèves doivent aussi réaliser qu’un pourcentage représente un rapport à 100 (par exemple, 30 % représente le rapport 30 :100). Il est important de souligner qu’un résultat exprimé en pourcentage ne signifie pas que la quantité en question est nécessairement composée de 100 parties, comme expliqué dans le tableau suivant.
Lien entre le pourcentage et la quantité 100
| Représentation | Pourcentage | Notes pédagogiques |
|---|---|---|
  |
75 % des cercles sont verts. | Même si 75 % des cercles sont verts, cela ne veut pas dire qu’il y a 100 cercles dans l’ensemble. Cependant, s’il y avait 100 cercles, il y aurait 75 cercles verts. De plus, la fraction des cercles qui sont verts est équivalente à \(\frac{{75}}{{100}}\) (par exemple, \(\frac{3}{4}\; = \;\frac{{75}}{{100}}\) et \(\frac{{150}}{{200}}\; = \;\frac{{75}}{{100}}\)). |
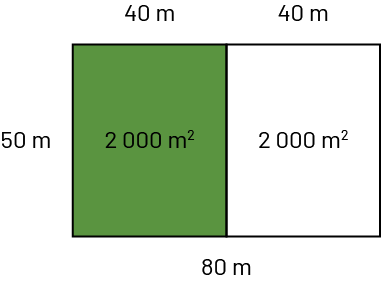 Image Un rectangle de 50 mètres par 80 mètres est découpé en deux parties égales sur la
largeur : une partie verte et une partie blanche. Ces deux dernières mesurent respectivement 2 000 mètres
carrés ainsi que 50 mètres par 40 mètres. |
50 % du terrain est recouvert de pelouse. | Même si 50 % du terrain est recouvert de pelouse, on ne peut pas affirmer que le terrain a une aire de 100 m2. Mais on peut affirmer que pour chaque 100 m2 de terrain, 50 m2 sont recouverts de pelouse. Ainsi, \(\frac{2\;000}{4\;000} = \frac{1}{2} = \frac{50}{100} = 50\) . |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 35.