B2.2 Comprendre et se rappeler des nombres carrés et de leur racine carrée de nombres utilisés couramment.
Habileté : comprendre et se rappeler des nombres carrés et de leur racine carrée de nombres utilisés couramment
En 8e année, les élèves établissent des liens entre les carrés parfaits et les racines carrées. La racine carrée est l’opération inverse d’une puissance dont l’exposant est 2.
- La racine carrée d’un nombre est un nombre qui, quand il est multiplié par lui-même, donne le nombre de départ.
- Les côtés d’un carré parfait correspondent aux racines de ce carré.
- Une puissance est le nombre de fois indiqué par l’exposant qu’un nombre est multiplié par lui-même.
Exemple
Racine carrée
\(\sqrt {16} \; = \;4\)
Puissance
\({4^2}\; = \;4\; \times \;4\; = \;16\)
En déterminant la longueur du côté d’un carré dont l’aire est donnée, on peut calculer la racine carrée de l’aire de ce carré.
Exemple
Détermine les dimensions d’un carré dont l’aire est de 36 unités carrées.
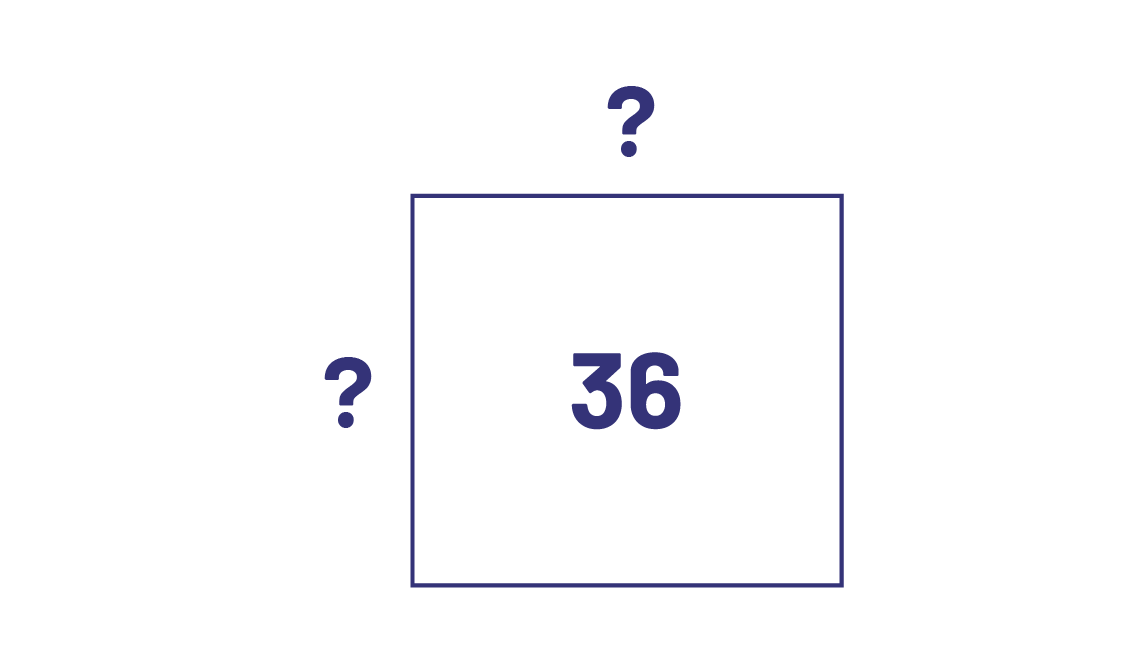
L’aire d’un carré s’obtient en multipliant la longueur de ses côtés.
\(A\; = \;c\; \times \;c\; = \;{c^2}\)
Je sais que l’aire est 36 et que \(6\; \times \;6\; = \;36\), alors les dimensions du carré sont \(6\; \times \;6\;\), soit \({6^2}\). Alors, \(\sqrt {36} \; = \;6\).
La racine carrée d’un nombre rationnel positif est toujours positive. La racine carrée d’un nombre rationnel négatif n’existe pas dans les nombres réels.
Exemple
\(\sqrt {25} \; = \;5,\;\;{\rm{car \;\; 5}}\; \times \;{\rm{5}}\;{\rm{ = }}\;\;{\rm{25 \;\; mais \;\; }} \sqrt {- 25} \) n’existe pas dans les nombres réels, car il n’y a aucun nombre réel multiplié par lui-même qui donne (–25).
L’élève doit être capable de manipuler des expressions contenant des entiers positifs et également des entiers négatifs. De plus, il doit comprendre la différence entre des expressions comme celles-ci :
- \({5^2}\; = \;5\; \times \;5\; = \;25\)
- \({\left( {- 5} \right)^2}\; = \;\left( {(- 5)\; \times \;(- 5)} \right)\; = \;25\)
- \(- ({5^2})\; = \;- {\left( {5\; \times \;5} \right)^2}\; = \;(- 25)\)
*source d’erreur très fréquente
Voici les représentations de tous les carrés parfaits de 1 à 144, ainsi que leur racine carrée positive. Les carrés et les racines carrées sont des opérations inverses.
| Carré parfait | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Repésentation visuelle |
1 11 |
2 24 |
3 39 |
4 416 |
5 525 |
6 636 |
7 749 |
8 864 |
9 981 |
10 10100 |
11 11121 |
12 12144 |
| Produit des côtés des carrés | \(1\; \times \;1\) | \(2\; \times \;2\) | \(3\; \times \;3\) | \(4\; \times \;4\) | \(5\; \times \;5\) | \(6\; \times \;6\) | \(7\; \times \;7\) | \(8\; \times \;8\) | \(9\; \times \;9\) | \(10\; \times \;10\) | \(11\; \times \;11\) | \(12\; \times \;12\) |
| Puissance sous sa forme exponentielle | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 | 102 | 112 | 122 |
| Racine carrée | \(\sqrt 1 \; = \;1\) | \(\sqrt 4 \; = \;2\) | \(\sqrt 9 \; = \;3\) | \(\sqrt {16} \; = \;4\) | \(\sqrt {25} \; = \;5\) | \(\sqrt {36} \; = \;6\) | \(\sqrt {49} \; = \;7\) | \(\sqrt {64} \; = \;8\) | \(\sqrt {81} \; = \;9\) | \(\sqrt {100} \; = \;10\) | \(\sqrt {121} \; = \;11\) | \(\sqrt {144} \; = \;12\) |
Connaissance : racine carrée (d’un nombre)
Nombre qui, lorsqu’il est multiplié par lui-même, donne le nombre (le carré). Par exemple, 3 est la racine carrée de 9, car \(3\; \times \;3\; = \;9\).
Note : Déterminer la longueur d’un côté d’un carré dont l’aire est donnée, c’est calculer la racine carrée de ce nombre. Le nom du signe utilisé pour l’écriture des racines carrées est radical. Le radicande est le nombre qui se situe sous le radical.
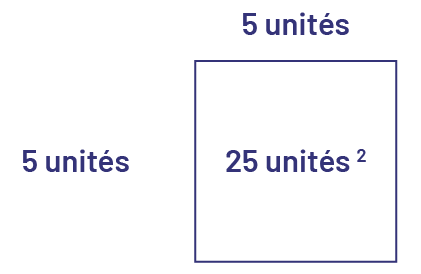
\(\sqrt {25} \; = \;5\)
La racine carrée de 25 est 5 puisque 5 × 5 = 5 2 = 25.
25 est un nombre carré ou un carré
parfait et 5 est sa racine carrée.
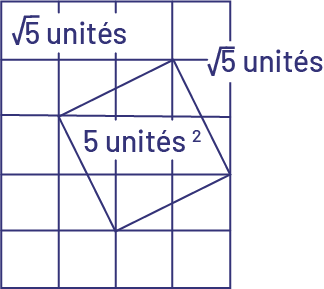Image Un rectangle est constitué de cinq rangées de quatre
carrés. Dans la première rangée, il est écrit racine carrée de cinq unités. À la jonction de la première à la
deuxième rangée, il est écrit racine carrée de cinq unités. Dans les deuxième, troisième et quatrième rangées
s’imbrique un carré tourné de travers sur son côté gauche, dans lequel il est écrit cinq unités carrées.
La racine carrée de 5 est \(\sqrt 5 \) car la racine carrée dont le radicande n’est pas un carré parfait est irrationnelle et s’exprime au moyen d’un radical ou d’un nombre décimal arrondi.
La racine carrée de 5 est \(\sqrt 5 \) car \(\sqrt 5 \; \times \;\sqrt 5 \; = \;{\sqrt 5 ^2}\; = \;5.\)
Source : En avant, les maths!, 8e année, CM, Nombres, p. 2.
Connaissance : carré parfait ou nombre carré
Carré parfait ou nombre carré. Un nombre entier multiplié par lui-même produit un nombre carré, ou un carré parfait, et peut être représenté par une puissance avec un exposant 2. Par exemple, 9 est un nombre carré parce que \(3\; \times \;3\; = \;9\;\;{\rm{ou}}\;\;{\rm{3}^2}\; = \;9\). Une représentation visuelle d’un nombre carré consiste à voir son aire comme le « carré de la longueur de son côté » (\({\rm{côté}} \times {\rm{côté }}\) ou \({c\;^2}\)).
Source : En avant, les maths!, 8e année, CM, Nombres, p. 3.