B2.2 Understand and recall commonly used square numbers and their square roots.
Skill: Understanding and Recalling Commonly Used Square Numbers and Their Square Roots
In Grade 8, students make connections between perfect squares and square roots. The square root is the inverse operation of a power whose exponent is 2.
- The square root of a number is a number that, when multiplied by itself, gives the starting number.
- The sides of a perfect square correspond to the roots of that square.
- A power is the number of times indicated by the exponent that a number is multiplied by itself.
Example
Square Root
\(\sqrt {16} \; = \;4\)
Power
\({4^2}\; = \;4\; \times \;4\; = \;16\)
To determine the length of the side of a square with a given area, we calculate the square root of the area of that square.
Example
Determine the dimensions of a square with an area of 36 square units.
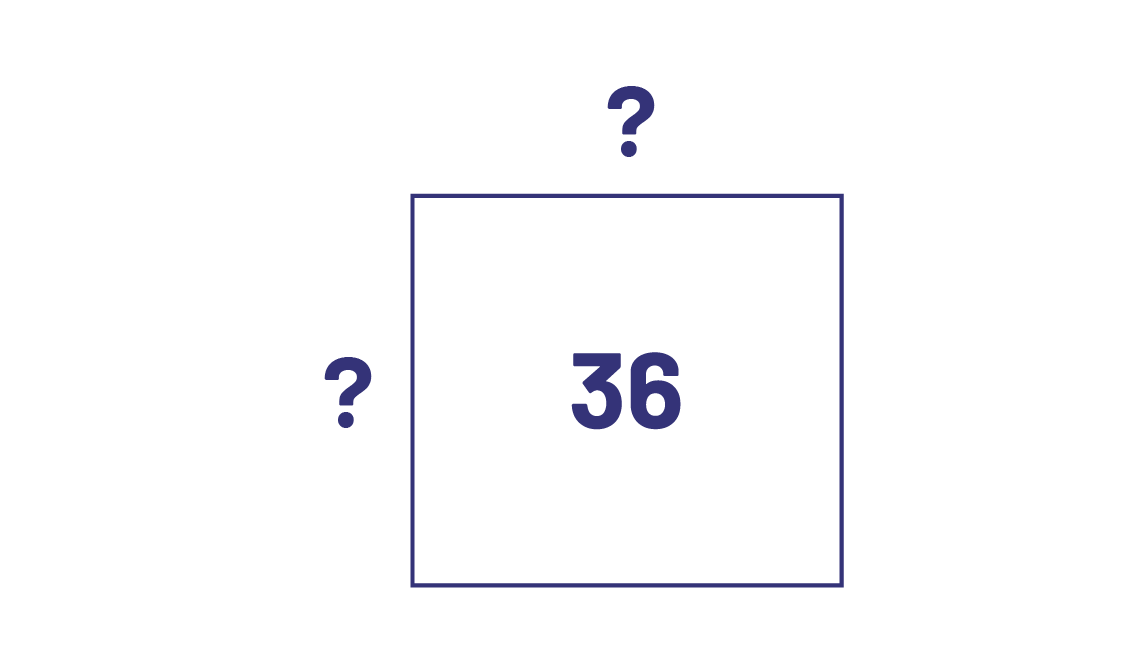
The area of a square is obtained by multiplying the length of its sides.
\(A\; = \;c\; \times \;c\; = \;{c^2}\)
I know that the area is 36 and that \(6\; \times \;6\; = \;36\), so the dimensions of the square are \(6\; \times \;6\;\), or \({6^2}\). Then, \(\sqrt {36} \; = \;6\).
The square root of a positive rational number is always positive. The square root of a negative rational number does not exist in real numbers.
Example
\(\sqrt {25} \; = \;5,\;{\rm{since \; \;5}}\; \times \;{\rm{5}}\;{\rm{ = }}\;{\rm{25 \; but \; }} \sqrt {- 25} \) does not exist in real numbers, because there is no real number multiplied by itself that gives –25.
The student should be able to manipulate expressions containing positive integers and also negative integers. In addition, they should understand the difference between expressions such as these:
- \({5^2}\; = \;5\; \times \;5\; = \;25\)
- \({\left( {- 5} \right)^2}\; = \;\left( {(- 5)\; \times \;(- 5)} \right)\; = \;25\)
- \(- ({5^2})\; = \;- {\left( {5\; \times \;5} \right)^2}\; = \;(- 25)\)
*very frequent source of error
Here are the representations of all the perfect squares from 1 to 144, as well as their positive square root. Squares and square roots are inverse operations.
| Perfect Square | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Visual Representation |
1 11 |
2 24 |
3 39 |
4 416 |
5 525 |
6 636 |
7 749 |
8 864 |
9 981 |
10 10100 |
11 11121 |
12 12144 |
| Product of the Sides of the Squares | \(1\; \times \;1\) | \(2\; \times \;2\) | \(3\; \times \;3\) | \(4\; \times \;4\) | \(5\; \times \;5\) | \(6\; \times 6\) | \(7\; \times 7\) | \(8\; \times \;8\) | \(9\; \times \;9\) | \(10\; \times \;10\) | \(11\; \times \;11\) | \(12\; \times \;12\) |
| Power in its Exponential Form | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 | 102 | 112 | 122 |
| Square Root | \(\sqrt 1 \; = \;1\) | \(\sqrt 4 \; = \;2\) | \(\sqrt9 = \;3\) | \(\sqrt {16} \; = \;4\) | \(\sqrt {25} \; = \;5\) | \(\sqrt {36} \; = \;6\) | \(\sqrt {49} \; = \;7\) | \(\sqrt {64} \; = \;8\) | \(\sqrt {81} \; = \;9\) | \(\sqrt {100} \; = \;10\) | \(\sqrt {121} \; = \;11\) | \(\sqrt {144} \; = \;12\) |
Knowledge: Square Root
A number that, when multiplied by itself, gives the number (square). For example, 3 is the square root of 9, because \(3 \times \;3 = \;9\).
Note: Determining the length of a side of a square where the area is given is calculated by finding the square root of the area. The name of the sign used for writing square roots is radical. The radicand is the number below the radical.
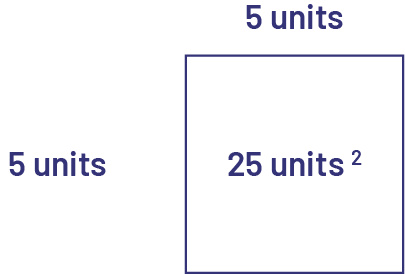
\(\sqrt {25} \; = \;5\)
The square root of 25 is 5 since because \(5 \;\times\; 5\; =\; 25 \). 25 is a square number or perfect square because 5 is its square root.
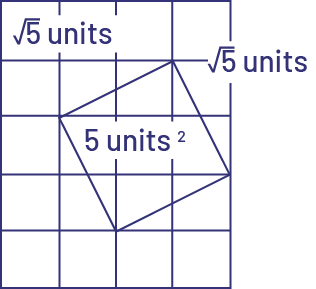
The square root of 5 is \(\sqrt 5 \) because the square root whose radicand is not a perfect square is irrational and is expressed as a radical or rounded decimal number.
Knowledge: Perfect Square or Square Number
A whole number multiplied by itself produces a square number, or a perfect square, and can be represented by a power with an exponent of 2. For example, 9 is a square number because \(3\; \times \;3 \;=\;9\;{\rm{or}}\;{\rm{3}^2}\;=\;9\). A visual representation of a square number is to view its area as the "square of its side length" (\({\rm{side}} \times {\rm{side }}\) or \({c ^2}\)).
Source: translated from En avant, les maths! 8e, CM, Nombres, p. 3.
