B2.3 Utiliser des stratégies de calcul mental pour multiplier et diviser des nombres naturels et des nombres décimaux jusqu’aux millièmes par des puissances de 10, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental pour multiplier et diviser des nombres naturels et des nombres décimaux jusqu’aux millièmes par des puissances de 10, et expliquer les stratégies utilisées
Calcul mental
La vie quotidienne présente de nombreuses occasions d’effectuer des opérations sur les nombres décimaux. Par exemple, les achats et les mesures font appel aux nombres décimaux. L’habileté à estimer et l’habileté à calculer mentalement sont des caractéristiques du sens du nombre et du sens des opérations. Diverses stratégies de calcul mental peuvent être utilisées, dont l’arrondissement, la décomposition et l’utilisation de repères.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 91.
Le calcul mental comprenant la multiplication et la division des nombres naturels et des nombres décimaux par des puissances de dix repose sur le rapport constant de 10 : 1 qui existe entre les valeurs de position.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Les élèves du cycle moyen ont déjà une expérience du concept de multiplication et comprennent que la multiplication de nombres naturels a pour effet de générer un produit supérieur aux quantités en cause, sauf dans les situations de multiplications par 1 et par 0. Elles et ils sont alors souvent surpris de constater qu’une multiplication dont l’un des facteurs est un nombre décimal inférieur à 1 donne un produit inférieur à l’autre facteur (par exemple, \(10\; \times \;0,1\; = \;1\; \) et \(20 \times 0,10 = 2\)).
Ces résultats sont surprenants pour quiconque ne traite pas les nombres en contexte ou n’a pas acquis une compréhension de la multiplication lui permettant d’expliquer de tels résultats.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 79.
Lorsqu’on multiplie un nombre naturel par 0,1 la valeur devient 10 fois plus petite, qui est la même chose que diviser par 10.
Lorsqu’on multiplie un nombre naturel par 0,01, la valeur devient 100 fois plus petite, qui est la même chose que diviser par 100.
Lorsqu’on multiplie un nombre par 0,001, la valeur devient 1 000 fois plus petite, qui est la même chose que diviser par 1 000.
Multiplication effectuée à l’aide du tableau de valeur de position
\[\ 23 \times 0,1 = 2,3\]
Je visualise un déplacement d’une colonne vers la droite dans le tableau de valeur de position.
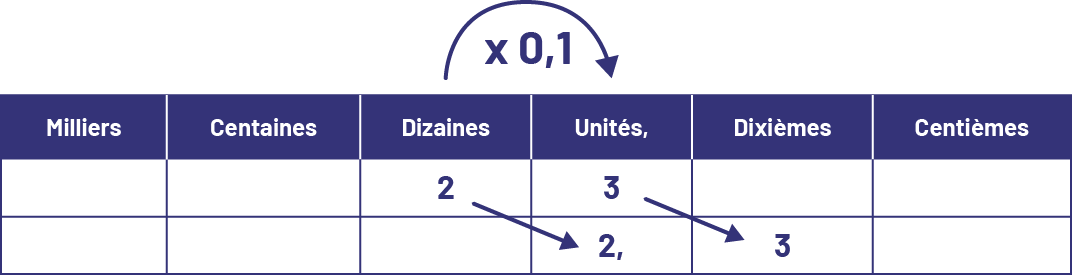Image Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit :
milliers, centaines, dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre
deux, relié par une flèche à la deuxième case des unités laquelle contient aussi le chiffre deux. Dans la première
case des unités, il y a le chiffre trois, relié par une flèche à la deuxième case des dixièmes laquelle contient aussi
le chiffre trois. Toutes les autres cases sont vides. Au-dessus de la colonne unités, il est écrit fois zéro virgule
un.
\[\ 23 \times 0,01 = 0,23\]
Je visualise un déplacement de deux colonnes vers la droite dans le tableau de valeur de position.
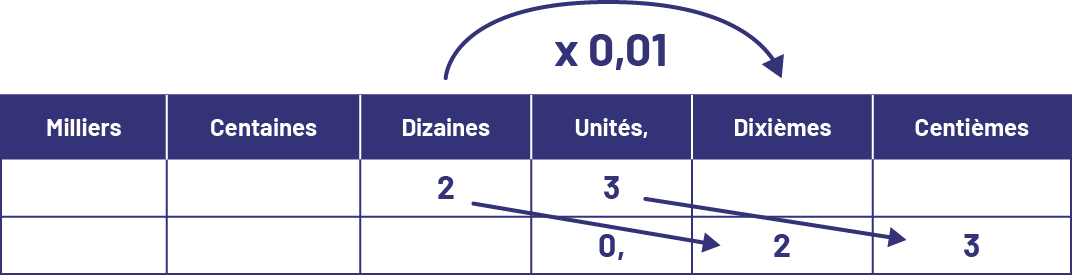Image
Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines,
dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une
flèche à la deuxième case des dixièmes, qui est vide. Dans la première case des unités, il y a le chiffre trois, relié
par une flèche à la deuxième case des centièmes, qui est vide. Dans la deuxième case des unités, il y a un zéro avec
une virgule. Toutes les autres cases sont vides. Au-dessus du tableau, entre unités et dixièmes, il est écrit fois
zéro virgule zéro un.
Multiplication effectuée à l’aide de la division
\[\ 23 \times 0,1 = 2,3\]
Pour effectuer \(23\; \times \;0,1\;\), je visualise le nombre 23 divisé en 10 groupes égaux. Je décompose 23 en 20 + 3.
\(\begin{array}{l}20\; \div \;10\; = \;2\\3\; \div \;10\; = \;0,3\\2\; + \;0,3\; = \;2,3\end{array}\)
Donc, dans chacun des groupes de 10, il y a 2,3.
\[230\; \times \;0,01\; = \;2,3\]
Pour effectuer \(230\; \times \;0,01\;\), je visualise le nombre 230 divisé en 100 groupes égaux. Je décompose 230 en 200 + 30.
Donc, dans chacun des groupes de 100, il y a 2,3.
Source : adapté de En avant, les maths!, 5e année, ML, Nombres, p. 5-6.
Lorsqu’on multiplie un nombre naturel ou un nombre décimal par une puissance positive de 10, la valeur devient plus grande (déplacement d’une position) pour chaque multiplication par 10.
- \( \times \;{10^1}\) : un déplacement d’une position vers la gauche
- \( \times \;{10^2}\) : un déplacement de deux positions vers la gauche
- \( \times \;{10^3}\) : un déplacement de trois positions vers la gauche
Lorsqu’on divise un nombre naturel ou un nombre décimal par une puissance positive de 10, la valeur devient plus petite (déplacement d’une position) pour chaque multiplication par 10.
- ÷ 101 : un déplacement d’une position vers la droite (× 0,1)
- ÷ 102 : un déplacement de deux positions vers la droite (× 0,01)
- ÷ 103 : un déplacement de trois positions vers la droite (× 0,001)
Ceci est évident lorsqu’on utilise un tableau de valeurs de position.
Ainsi, l’élève peut écrire son nombre initial au bon endroit dans les bonnes cases du tableau et poursuivre avec ses calculs mentaux en déplaçant les chiffres selon les positions. Ce visuel lui permettrait d’appliquer plus facilement les stratégies de calcul mental et ainsi les expliquer.
Exemple
Nombre initial : 645,123
- 645,123 × 101
- 645,123 × 102
- 645,123 × 103
- 645,123 ×104
- 645,123 ÷ 101 ou 645,123 × 0,1
- 645,123 ÷ 102 ou 645,123 × 0,01
- 645,123 ÷ 103 ou 645,123 × 0,001
| Unités de millions | Centaines de mille | Dizaines de mille | Unités de mille | Centaines | Dizaines | Unités, | Dixièmes | Centièmes | Millièmes | |
|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 4 | 5, | 1 | 2 | 3 | |||||
| a) | 6 | 4 | 5 | 1, | 2 | 3 | ||||
| b) | 6 | 4 | 5 | 1 | 2, | 3 | ||||
| c) | 6 | 4 | 5 | 1 | 2 | 3, | ||||
| d) | 6 | 4 | 5 | 1 | 2 | 3 | 0, | |||
| e) | 6 | 4, | 5 | 1 | 2 | |||||
| f) | 6, | 4 | 5 | 1 | ||||||
| g) | 0, | 6 | 4 | 5 |
Que remarquez-vous si je multiplie le nombre initial par 1 000? Par 10 000 ? Par 0,01? Par 0,001?
Connaissance : relation de valeur de position
C’est au début du cycle moyen que les élèves étudient pour la première fois la partie décimale d’un nombre. Elles et ils doivent alors approfondir leur compréhension de la valeur de position des chiffres et de la relation entre les valeurs de position. Les nombres décimaux font partie du quotidien et la compréhension des valeurs de position à la droite et à la gauche de la virgule est essentielle. La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.
Or, il est essentiel que les élèves reconnaissent la position des unités puisque c’est elle qui définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, les centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.
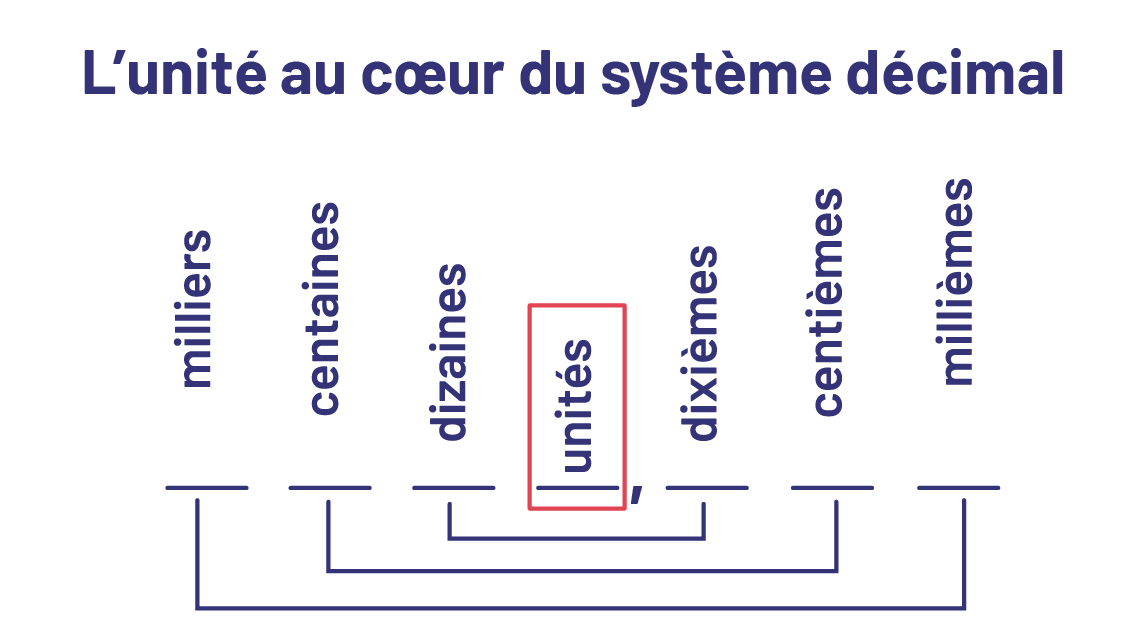Image Le schéma se présente comme suit : milliers, centaines,
dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le mot « unités » est encadré. Les mots « milliers » et «
millièmes » sont réunis par un trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et «
dixièmes ».
Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les dizaines représentent une quantité dix fois plus grande que l’unité, alors que les dixièmes représentent une quantité dix fois plus petite que l’unité. De même, la centaine est cent fois plus grande que l’unité, alors que le centième est cent fois plus petit que l’unité.
Note : Certains élèves ont l’impression que c’est la virgule qui est au centre du système décimal. Conséquemment, elles et ils ont tendance à appeler la première position à droite de la virgule, la position des unièmes plutôt que des dixièmes. Il est important que les élèves saisissent aussi la relation multiplicative par 10 qui existe entre les valeurs de position adjacentes. Elles et ils ont préalablement développé une compréhension de cette relation dans le cadre de l’étude des nombres naturels, soit que chaque position a une valeur 10 fois plus grande que celle à sa droite et 10 fois plus petite que celle à sa gauche.
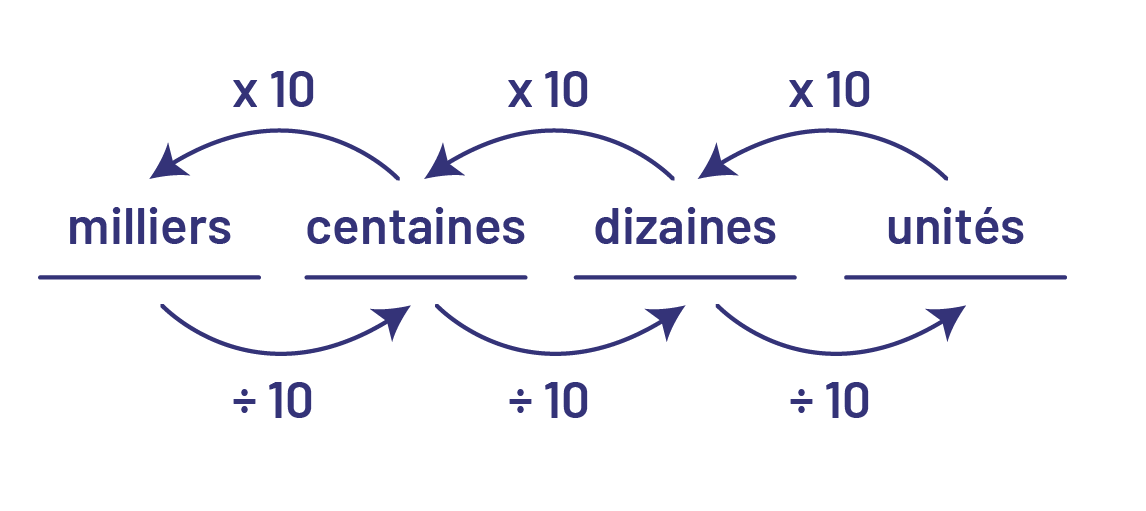Image Le schéma se présente comme suit, de gauche à droite : milliers,
centaines, dizaines, unités. En haut, chaque mot est relié à son précédent par une flèche courbe au-dessus de laquelle
il est écrit « fois dix ». En bas, chaque mot est relié au suivant par une flèche courbe sous laquelle il est écrit «
divisé par dix ».
Or, cette relation multiplicative est aussi vraie pour les positions décimales.
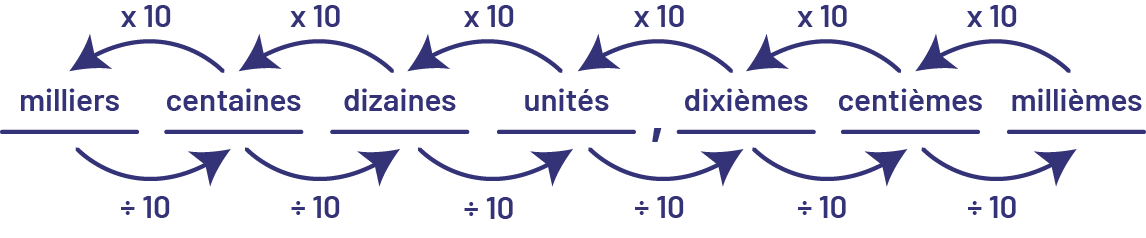Image Le
schéma se présente comme suit, de gauche à droite : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. En haut, chaque mot est relié à son précédent par une flèche courbe au-dessus de laquelle il est
écrit « fois dix ». En bas, chaque mot est relié au suivant par une flèche courbe sous laquelle il est écrit « divisé
par dix ».
Les élèves peuvent en développer une compréhension en effectuant des regroupements à l’aide du matériel de base dix. Il s’agit de démontrer que, tout comme 10 unités donnent 1 dizaine, 10 dixièmes donnent 1 unité et 10 centièmes donnent 1 dixième, et ainsi de suite.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 51-52.