B2.3 Use mental math strategies to multiply and divide whole numbers and decimal numbers up to thousandths by powers of ten, and explain the strategies used.
Skill: Using Mental Math Strategies to Multiply and Divide Whole Numbers and Decimal Numbers to Thousandths by Powers of 10, and Explain the Strategies Used
Mental Math
Daily life presents many opportunities to perform operations with decimal numbers. For example, shopping and measuring involve decimal numbers. Having solid estimation and mental math skills are characteristics of good number sense and operation sense. A variety of mental math strategies can be used, including rounding, decomposing, and using benchmarks.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 91.
Mentally multiplying and dividing whole numbers and decimals by powers of ten builds on the constant 10:1 ratio between place value columns.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Junior students already have experience with the concept of multiplication and understand that multiplying whole numbers results in a product that is greater than the quantities involved, except in situations involving multiplication by 1 and by 0. They are then often surprised to find that a multiplication in which one of the factors is a decimal number less than 1 gives a product less than the other factor (for example, \(10\; \times \;0.1\; = \;1\;{\rm{\;and\;}}\;{\rm{20}}\; \times \;{\rm{0}}{\rm{.10}}\;{\rm{ = } }\;{\rm{2}}\)).
These results are surprising to anyone who does not deal with numbers in context or has not developed an understanding of multiplication to explain such results.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 79.
When you multiply a whole number by 0.1 the value becomes one tenth as large, which is the same as dividing it by 10.
When you multiply a whole number by 0.01, the value becomes one hundredth as large, which is the same as dividing it by 100.
When you multiply a whole number by 0.001, the value becomes one thousandth as large, which is the same as dividing it by 1000.
Multiplication Performed Using the Place Value Chart
\(23 \times 0.1 = 2.3\)
To multiply by one tenth, I visualized a shift of the number one column to the right in the place value chart.
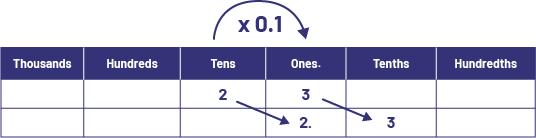
\(23 \times 0.01 = 0.23\)
To multiply by one hundredth, I visualized a shift of the number two columns to the right in the place value chart.
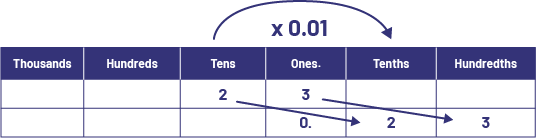
Multiplication Using Division
\(23 \times 0.1 = 2.3\)
To perform \(23\; \times \;0.1\;\), I visualized the number 23 divided into 10 equal groups. To make it easier I decompose 23 into 20 + 3.
\(\begin{array}{l}20\; \div \;10\; = \;2\\3\; \div \;10\; = \;0.3\\2\; + \; 0.3\;=\;2.3\end{array}\)
So, in each group of 10, there are 2.3.
\(230 \times 0.01 = 2.3\)
To perform \(230\; \times\; 0.01 \), I visualized the number 230 divided into 100 equal groups. I decompose 230 into 200 + 30.
So in each of the groups of 100, there are 2.3.
Source: adapted and translated from En avant, les maths!, 5e, ML, Nombres, p. 5-6.
When a whole number or decimal number is multiplied by a positive power of 10, the value becomes ten times larger and the entire number shifts one position to the left for each multiplication by 10.
- \( \times \;{10^1}\): moving one position to the left
- \( \times \;{10^2}\): a move of two positions to the left
- \( \times \;{10^3}\): a move of three positions to the left
When dividing a whole number or a decimal number by a positive power of 10, the value becomes ten times smaller and the entire number shifts one position to the right for each multiplication by 10.
- ÷ 101: moving one position to the right (× 0.1)
- ÷ 102: a move two positions to the right (× 0.01)
- ÷ 103: a move three positions to the right (× 0.001)
This is evident when using a place value chart.
This way, students can write their initial number in the place value chart and use their mental math to move the numbers according to the multiplier. This visual makes it easier for them to apply mental math strategies and explain them.
Example
Initial number: 645.123
- 645.123 × 101
- 645.123 × 102
- 645.123 × 103
- 645.123 ×104
- 645.123 ÷ 101 or 645.123 ×0.1
- 645.123 ÷ 102 or 645.123 ×0.01
- 645.123 ÷ 103 or 645.123 × 0.001
| Millions | Hundreds of Thousand | Tens of Thousand | Thousands | Hundreds | Tens | Ones. | Tenths | Hundredths | Thousandths | |
|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 4 | 5. | 1 | 2 | 3 | |||||
| a) | 6 | 4 | 5 | 1. | 2 | 3 | ||||
| b) | 6 | 4 | 5 | 1 | 2. | 3 | ||||
| c) | 6 | 4 | 5 | 1 | 2 | 3. | ||||
| d) | 6 | 4 | 5 | 1 | 2 | 3 | 0. | |||
| e) | 6 | 4. | 5 | 1 | 2 | |||||
| f) | 6. | 4 | 5 | 1 | ||||||
| g) | 0. | 6 | 4 | 5 |
Ask students: "What do you notice if I multiply the initial number by 1 000? By 10 000? By 0.01? By 0.001?
Knowledge: Place Value Relationship
The beginning of the Junior Division is the first time students study the decimal part of a number. They need to deepen their understanding of the place values of the numbers and the relationship between the place values. Decimal numbers are part of everyday life and understanding the place values to the right and left of the decimal point is essential. The decimal point plays a significant role in decimal notation. It separates the whole part from the decimal part and thus indicates the position of the ones.

It is essential that students recognize the position of the ones, since it defines the whole, from which the tenths, hundredths and thousandths are formed on the one hand, and the tens, hundreds and thousands on the other. We can therefore say that the ones, identified by the decimal point, is at the heart of the decimal system, and there is symmetry around it.
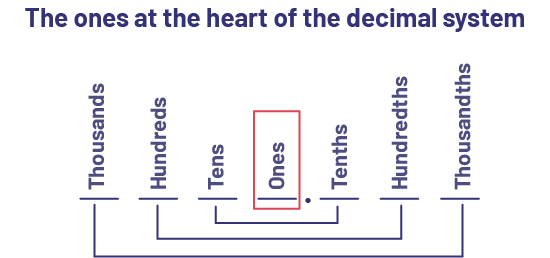
This recognition of the role of the units digit is evidenced by the name prefixes given to the place value of the digits on either side of the unit digit. Thus, tens represent a quantity ten times greater than the unit, while tenths represent a quantity ten times smaller than the unit.
Note: Some students are under the impression that the decimal point is the centre of the decimal system. As a result, they tend to call the first position to the right of the decimal point the oneth rather than the tenth position. It is also important that students understand the \( \times\; 10 \) multiplicative relationship that exists between adjacent place values. Students should have previously developed an understanding of this relationship in the study of whole numbers, such that each place has a value 10 times greater than the one to its right and 10 times smaller than the one to its left.
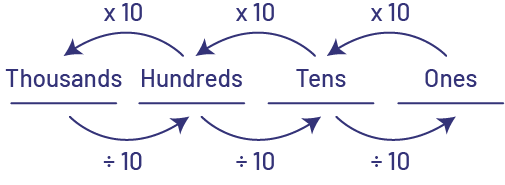
This multiplicative relationship is true for all positions.
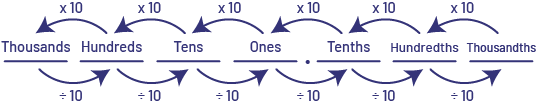
Students can develop an understanding of this relationship by doing groupings using base ten blocks. The idea is to demonstrate that just as 10 ones yield 1 ten, 10 tenths yield 1 one and 10 hundredths yield 1 tenth, and so on.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 51-52.
