B2.4 Additionner et soustraire des nombres entiers, en utilisant des stratégies appropriées, dans divers contextes.
Habileté : représenter, décrire et résoudre des additions et des soustractions de nombres entiers
En 7e année, l’élève est amené à additionner et à soustraire des nombres entiers en utilisant différentes représentations (jetons bicolores, droite numérique) et des stratégies de calcul qui lui permettront de généraliser des règles de calcul. L’utilisation de jetons bicolores et de la droite numérique est essentielle pour illustrer l’addition et la soustraction de nombres entiers. En utilisant ces modèles, l’élève se crée des représentations visuelles des opérations à effectuer et peut mieux comprendre la raison d’être des différentes règles qui régissent l’addition et la soustraction des nombres entiers. Plutôt que d’enseigner des règles, il est préférable que l’élève, à la suite de certaines observations, puisse les généraliser. Les règles de calcul concernant les nombres entiers constituent le point d’arrivée et non le point de départ de l’enseignement et de l’apprentissage de ces nombres.
Source : Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 7e année, Module 3, Série 1, Introduction, p. 15.
Comme pour les nombres naturels, l’addition de nombres entiers est commutative. Alors, l’ordre dans lequel les nombres entiers sont écrits dans une addition n’a pas d’importance.
Cependant, comme pour les nombres naturels, la commutativité ne s’applique pas à la soustraction. L’ordre dans lequel les nombres entiers sont écrits dans une soustraction est important.
Lors de l’écriture d’une égalité, les nombres entiers sont souvent placés entre parenthèses, par exemple \(\ { 3} \; - {(- 2)} \; = \; { 5} \).
- Si un signe n’est pas inclus, le nombre est considéré comme positif.
- Ces conventions aident à réduire la confusion entre le nombre et l’opération.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Modèle des jetons bicolores
Une couleur représente les nombres positifs et une autre représente les nombres négatifs.

Dans ce modèle, deux jetons de couleurs opposées s’annulent ou donne 0.
Exemples
\((- 5)\; + \; 3\;\)
Je représente chaque terme à l’aide de jetons bicolores, soit 5 jetons rouges et 3 jetons blancs.
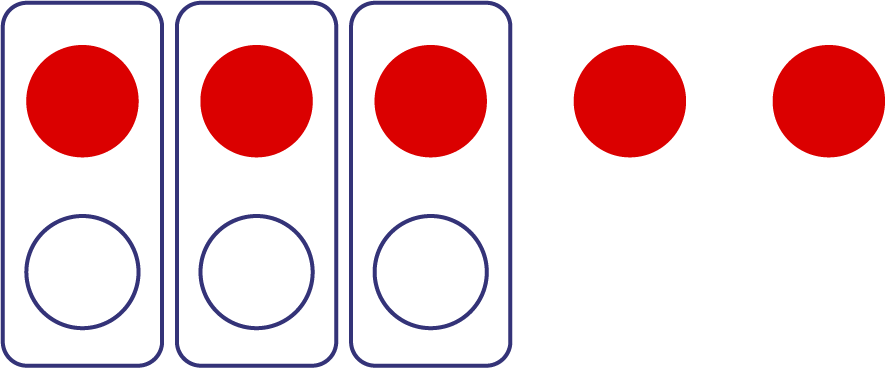
J’associe un jeton rouge à un jeton blanc pour obtenir des zéros puisqu’ils s’annulent. En tout, il y a 3 zéros. Cet ensemble de jetons représente le nombre entier \((- 2)\). Alors, \((- 5)\; + \; 3\; = \;(- 2)\).
\((- 5)\; + \;(- 3)\;\)
Je représente chaque terme à l’aide de jetons bicolores, soit 5 jetons rouges et 3 jetons rouges.

En tout, il y a 8 jetons rouges. Cet ensemble de jetons représente le nombre entier \((- 8)\). Alors, \((- 5)\; + \;(- 3)\; = \;(- 8)\) .
\(5\; + \;(- 3)\;\)
Je représente chaque terme à l’aide de jetons bicolores. J’ai 5 jetons blancs et 3 jetons rouges.

J’associe un jeton rouge à un jeton blanc pour obtenir des zéros puisqu’ils s’annulent. En tout, il y a 3 zéros. Cet ensemble de jetons représente le nombre entier \( 2\). Alors, \(5\; + \;(- 3)\; = {\rm{2}}\).
\(5\; - \;(- 3)\;\)
J'ai cinq jetons blancs.

Je veux enlever 3 jetons rouges mais je n'en ai pas alors, je les ajoute en ajoutant des paires de 0.

Maintenant, je peux enlever mes trois jetons rouges.

Il me reste huit jetons blancs.

Cet ensemble de jetons représente le nombre entier 8. Alors, \(5\; - (-3)\; = \;8\).
Modèle de la droite numérique
Dans ce modèle, les entiers sont représentés par des flèches. La direction de la flèche détermine si la valeur représente une quantité positive ou négative. La longueur (toujours une valeur positive) de la flèche représente la quantité, et sa direction, le signe.
Exemple
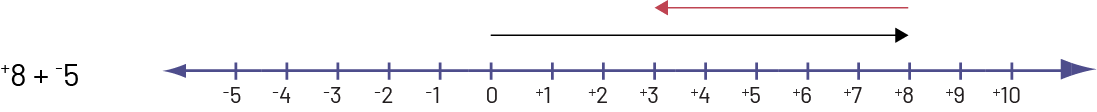
La flèche noire qui est positive (pointe vers la droite) représente \( 8\).
La flèche rouge qui est négative (pointe vers la gauche) représente \((- 5)\).
Lorsque deux nombres entiers positifs sont additionnés, le résultat est positif. Cela peut être visualisé sur une droite numérique comme :
- deux flèches se déplaçant dans une direction positive (vers la droite ou vers le haut);
- une flèche se déplaçant dans une direction positive à partir d’un nombre de départ positif.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
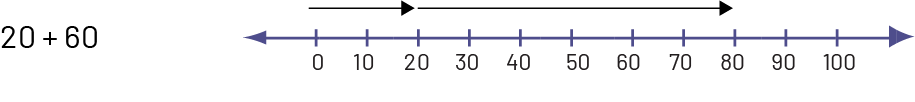
À partir de zéro, l’élève fait un bond de 20 et par la suite lui ajoute un bond de 60 donc la position finale représente la somme qui équivaut à 80. Alors, \(60\; + \;20\; = \;80\).
Lorsque deux nombres entiers négatifs sont additionnés, le résultat est négatif. Cela peut être visualisé sur une droite numérique comme :
- deux flèches se déplaçant dans une direction négative (vers la gauche ou vers le bas);
- une flèche se déplaçant dans une direction négative à partir d’une position de départ négative.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
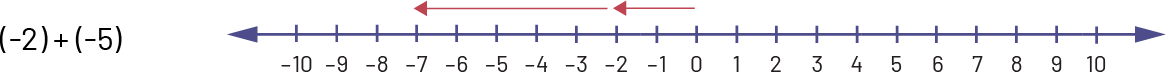
À partir de 0, l’élève dessine une flèche rouge de 2 unités vers la gauche. À partir du \((- 2)\), il se déplace d’un autre 5 unités vers la gauche. L’élève s’arrête à \((- 7)\). Alors, \(\left( {- 2} \right)\; + \;\left( {- 5} \right)\; = \;(- 7)\).
Lorsque des nombres entiers positifs et négatifs sont additionnés, le résultat est négatif si la valeur absolue du nombre entier négatif est supérieure à la valeur absolue du nombre positif. Cela peut être visualisé sur une droite numérique comme :
- une flèche se déplaçant dans une direction positive et l’autre flèche de plus grande amplitude se déplaçant dans une direction négative;
- une flèche se déplaçant dans une direction négative à partir d’une position de départ positive (la pointe est à la gauche ou au-dessous de zéro);
- une flèche se déplaçant dans une direction positive à partir d’une position de départ négative (la pointe de la flèche est à la gauche ou au-dessous de zéro).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
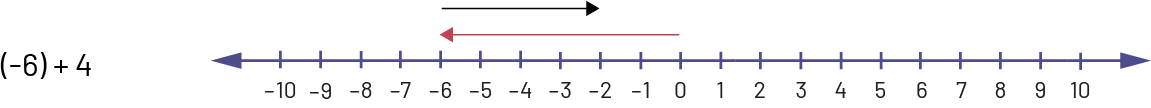
À partir de 0, l’élève dessine une flèche rouge de 6 unités vers la gauche. À partir du -6, il se déplace de 4 unités vers la droite en dessinant une flèche noire. L’élève s’arrête à \((- 2)\). Alors, \(\left( {- 6} \right)\; + \;\left( 4 \right)\; = \;(- 2)\).
Lorsque des nombres entiers positifs et négatifs sont additionnés, le résultat est positif si la valeur absolue du nombre entier positif est supérieure à la valeur absolue du nombre entier négatif. Cela peut être visualisé sur une droite numérique comme :
- une flèche se déplaçant dans une direction négative et l’autre flèche de plus grande amplitude se déplaçant dans une direction positive;
- une flèche se déplaçant dans une direction positive à partir d’une position de départ négative (la pointe de la flèche est à la droite ou au-dessus du zéro);
- une flèche se déplaçant dans une direction négative à partir d’une position de départ positive (la pointe de la flèche est à la droite ou au-dessus de zéro).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple

À partir de 0, l’élève dessine une flèche rouge de 3 unités vers la gauche. À partir du \((- 3)\), il se déplace de 7 unités vers la droite en dessinant une flèche noire. L’élève s’arrête à 4. Alors \((- 3)\; + ( 7) = \;4\).
La soustraction sur la droite numérique peut aussi être vue comme l’écart entre les 2 nombres.
Exemple
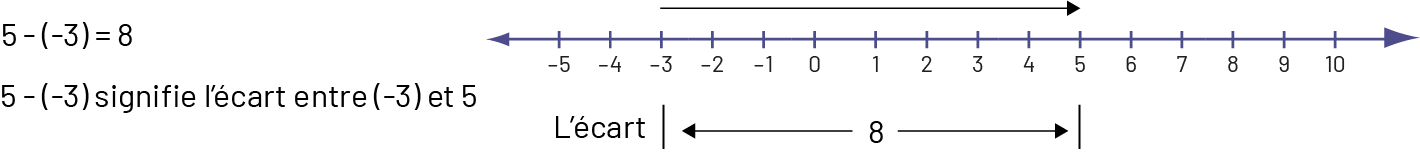 Image Une double droite numérique est graduée de moins cinq à plus dix.
Au-dessus de la droite, une flèche part de moins trois et se rend à plus cinq. Sous la droite, le chiffre huit
s’accompagne d’une double flèche gauche-droite qui couvre le même écart que la flèche au-dessus de la droite.
Image Une double droite numérique est graduée de moins cinq à plus dix.
Au-dessus de la droite, une flèche part de moins trois et se rend à plus cinq. Sous la droite, le chiffre huit
s’accompagne d’une double flèche gauche-droite qui couvre le même écart que la flèche au-dessus de la droite.
Les situations de la vie quotidienne qui comprennent des nombres entiers positifs et négatifs fournissent un point de départ pour comprendre comment elles et ils décrivent un changement (par exemple, température, déplacements d’ascenseurs, niveau de la mer, pointage au golf, acquisition et perte d’argent, pas vers l’avant et l’arrière).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple 1
Selon le bulletin météo, il fait présentement \((- 4)\;^\circ {\rm{C}}\) à Iqaluit. La température augmentera de 9 degrés au cours de la journée. Quelle est la température maximale prévue?
Voici un exemple de solution possible :
 Image Un thermomètre affiche une graduation de moins quatre à cinq
degrés Celsius en montrant le zéro entre les deux. À gauche, une flèche monte de moins quatre à cinq en indiquant neuf
degrés Celsius.
Image Un thermomètre affiche une graduation de moins quatre à cinq
degrés Celsius en montrant le zéro entre les deux. À gauche, une flèche monte de moins quatre à cinq en indiquant neuf
degrés Celsius.
Je sais que 5 °C, c’est 9 degrés de plus que \((- 4)\;^\circ {\rm{C}}\).
Donc, la température maximale prévue à Iqaluit est de 5 °C.
Source : Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 7e année, Module 3, Série 1, Activité 3 Addition de nombres entiers, p. 82.
Exemple 2
Au printemps, Patrick emprunte 75 $ à ses parents pour s’acheter un vélo. Pendant l’été, il économise en vue de rembourser ses parents. En septembre, il remet 25 $ à ses parents. En octobre, il leur remet 30 $. Dans quelle situation financière se trouve Patrick à la suite de son emprunt?
Voici des exemples de solutions possibles :
Dette : 75 $ ou \((- 75)\)
Argent économisé : 55 $ \(\left( {25\; + \;30\; = \;55} \right)\)ou 55
Patrick a donc remboursé 55 $ des 75 $ qu’il devait à ses parents.
\(\begin{align}(- 75)\; + \; 25\; + \; 30\; &= \;(- 75)\; + \; 55\\ &= \;\left( {(- 20)\; + \;(- 55)} \right)\; + \; 55\\ &= \;(- 20)\; + \;0\\ &= \;(- 20)\end{align}\)
Patrick doit encore 20 $ à ses parents.
Source : Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 7e année, Module 3, Série 1, Activité 3 Addition de nombres entiers, p. 78.
Connaissance : nombre entier
Les nombres entiers appartiennent à l’ensemble \(\Bbb{Z}\).
\(\Bbb{Z} = \left\{ { \ldots ,\; } \right.(-3),\;(- 2,)\;(- 1),\;0,\;1,\;2,\;3\left. \ldots \right\}\)
Chaque nombre entier est formé d’un nombre et d’un signe + ou - .
Chaque nombre entier a un opposé (par exemple, \(- 3\;\;\;{\rm{et}}\;\;\; 3\)). L’opposé d’un nombre positif est un nombre négatif de même quantité (valeur absolue), et vice versa.
Les signes + ou - sont associés au nombre. Ce ne sont pas des signes d’opération. Ainsi, le nombre \((- 4)\) se lit : l’opposé de 4 ou négatif 4.
Il n’y a pas d’espace entre le signe négatif « \(- \) » et le nombre 4, puisqu’il ne s’agit pas de l’opération de soustraction.
Zéro n’est ni un nombre positif ni un nombre négatif, car il est le seul nombre à être son propre opposé.
Sur la droite numérique, les nombres sont par ordre croissant de la gauche vers la droite et par ordre décroissant de la droite vers la gauche.
 Image Une droite numérique est graduée de moins vingt à plus vingt.
Au-dessus de la droite, du côté gauche, il est écrit « Nombres négatifs ». Au-dessus du zéro, il est écrit : «
Frontière entre les nombres positifs et négatifs ». Et du côté droit, il est écrit : « Nombres positifs ».
Image Une droite numérique est graduée de moins vingt à plus vingt.
Au-dessus de la droite, du côté gauche, il est écrit « Nombres négatifs ». Au-dessus du zéro, il est écrit : «
Frontière entre les nombres positifs et négatifs ». Et du côté droit, il est écrit : « Nombres positifs ».
Source : Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 7e année, Module 3, Série 1, Activité 1 Des nombres entiers sur la droite numérique, p. 35-37.
