B2.5 Additionner et soustraire des fractions, en utilisant des stratégies appropriées, dans divers contextes.
Habileté : additionner et soustraire des fractions avec et sans dénominateurs communs, à l’aide d’outils et de stratégies appropriés
Faire le lien entre les opérations sur les nombres naturels et celles sur les fractions
Les élèves ont déjà acquis une compréhension solide de l’addition et de la soustraction. Il est important de faire des liens entre les opérations sur les nombres naturels et celles sur les fractions. Par exemple, l’addition de 3 huitièmes et de 2 huitièmes est la même que celle de 3 bonbons et de 2 bonbons. Seule la notation est différente et plus complexe.
Valoriser les procédures informelles pour développer des stratégies
Il est important de valoriser les procédures informelles, car elles contribuent au développement du sens du nombre et du sens des opérations. Dans des situations qui impliquent des opérations, plusieurs élèves font appel à des algorithmes personnels plutôt qu’aux procédures. Par exemple, l’élève qui a un bon sens du nombre pourrait aborder l’addition de \(\frac{7}{8}\) d’un sandwich et de \(\frac{4}{8}\) d’un autre sandwich identique de cette façon : « Je sais qu’avec \(\frac{7}{8}\) d’un sandwich, il me manque \(\frac{1}{8}\) d’un sandwich pour avoir un sandwich complet. Alors, si j’ajoute \(\frac{1}{8}\) à \(\frac{7}{8}\), j’ai un entier et il me reste \(\frac{3}{8}\). Donc, \(\frac{7}{8}\; + \;\frac{4}{8}\; = \;1\frac{3}{8}\). »
Nature des opérations fondamentales
L’application d’une opération sur des nombres a pour effet de réorganiser les quantités en jeu. Il est très important que les élèves comprennent cette facette de la quantité lorsqu’elles et ils utilisent l’une ou l’autre des quatre opérations. Les élèves du cycle moyen ont eu l’occasion d’apprendre cette relation par rapport aux quatre opérations sur les nombres naturels. Dans l’addition, deux quantités sont mises ensemble pour former une nouvelle quantité. Dans une soustraction, on enlève une quantité d’une autre. On peut aussi reconnaître que l’on cherche une quantité par laquelle deux quantités données diffèrent.
Il faut beaucoup de temps pour construire un sens des opérations sur les fractions, car il faut réfléchir aux numérateurs, aux dénominateurs et aux touts en cause. Il faut donner aux élèves l’occasion de travailler avec des modèles concrets et semi-concrets et de développer un sens de l’ordre de grandeur des résultats avant de passer aux opérations mettant en cause les représentations symboliques.
Selon le programme-cadre, les élèves de 6e année voient l’addition et la soustraction de fractions avec et sans dénominateurs communs.
Pour l’addition et soustraction avec des fractions ayant un même dénominateur, il s’agit essentiellement de l’addition et de la soustraction d’objets ou de quantités de même nature.
Par exemple, dans \(\frac{3}{7}\; + \;\frac{2}{7}\; = \;\frac{5}{7}\), l’addition représente simplement 3 un septième + 2 un septième = 5 un septième, tout comme 3 pommes + 2 pommes = 5 pommes. Dans cet exemple, les septièmes sont comptés de la même façon que des pommes. On a 3 morceaux d’une certaine taille et 2 morceaux de la même taille, ce qui donne 5 morceaux de cette taille.
Effectuer l’addition de fractions devient plus complexe lorsque les fractions ont des dénominateurs différents, puisque les morceaux n’ont pas la même taille et ne sont pas de même nature.
La soustraction se traite de la même façon. Par exemple, si j’enlève 3 billes d’un sac qui en contient 5, il en reste 2. De même, si je soustrais 3 un huitième de 5 un huitième, il reste 2 un huitième (\(\frac{5}{8}\; - \;\frac{3}{8}\; = \;\frac{2}{8}\)).
L’addition de deux nombres naturels a pour effet d’augmenter les deux quantités initiales, tandis que la soustraction de deux nombres naturels a pour effet de diminuer la quantité initiale. Il est important que les élèves comprennent qu’il en est de même pour l’addition et la soustraction de fractions.
Cela leur permet de comprendre l’invraisemblance de certaines réponses obtenues à partir de procédures erronées. Par exemple, l’élève qui, pour calculer \(\frac{2}{3}\; + \;\frac{1}{3}\), additionne les numérateurs et les dénominateurs et obtient \(\frac{3}{6}\), devrait voir que cette réponse, qui est égale à \(\frac{1}{2}\), est inférieure à une des fractions initiales, soit \(\frac{2}{3}\).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 75-77.
 Description de la vidéo
Description de la vidéo
Description à venir
Explorer les opérations à l’aide de plusieurs modèles
Il est important pour les élèves d’apprendre les concepts liés aux fractions dans diverses situations à l’aide d’une variété de modèles tels que des modèles de surface, des modèles de longueur et des modèles d’ensemble. Il en est de même pour l’apprentissage des opérations sur les fractions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 76.
Lorsqu’on travaille avec les fractions, le plus important et parfois le plus difficile, c’est de bien représenter le tout. Avec du matériel concret ou semi-concret, l’effet visuel de l’addition et de la soustraction est renforcé. En puisant dans leurs expériences avec les nombres naturels et en se forgeant un sens de l’opération, les élèves peuvent reconnaître, par exemple, que l’ajout de deux tiers (\(\frac{2}{3}\)) à un tiers (\(\frac{1}{3}\)) donne trois tiers (\(\frac{3}{3}\)), soit le tout.
 Image Le tout est représenté par une languette rouge divisée en trois parties égales. Sous celle-ci,
il y a une languette de la même longueur divisée en trois parties égales : une violet pâle, qui représente un tiers,
et deux bleu marine, qui représentent deux tiers.
Image Le tout est représenté par une languette rouge divisée en trois parties égales. Sous celle-ci,
il y a une languette de la même longueur divisée en trois parties égales : une violet pâle, qui représente un tiers,
et deux bleu marine, qui représentent deux tiers.
Or, il n’est pas toujours clair pour les élèves que l’addition se fait par rapport au numérateur. Dans une situation où il reste trois huitièmes (\(\frac{3}{8}\)) d’une pizza et deux huitièmes (\(\frac{2}{8}\)) d’une autre pizza de même grandeur, on cherche combien il en reste en tout. Est-ce qu’on compte des huitièmes ou des seizièmes, puisque les pizzas comptaient seize morceaux en tout?
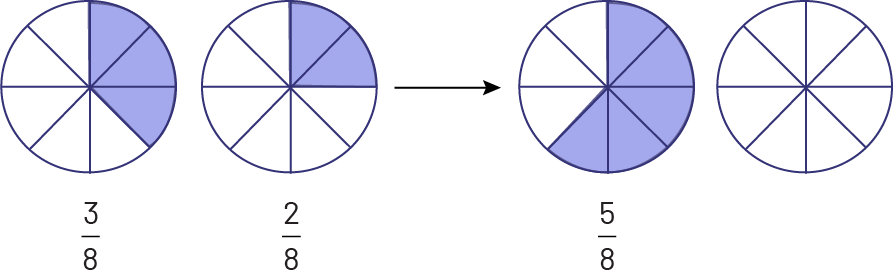 Image Quatre diagrammes circulaires sont placés côte à côte. Ils sont
tous divisés de la même façon, en huit parts égales. Le premier diagramme a trois parts violettes et cinq parts
blanches. Il indique trois huitièmes. Le deuxième a deux parts violettes et indique deux huitièmes. Une flèche le
relie au suivant. Le troisième a cinq parts violettes et indique cinq huitièmes. Et le quatrième est tout blanc et
n’indique aucune fraction.
Image Quatre diagrammes circulaires sont placés côte à côte. Ils sont
tous divisés de la même façon, en huit parts égales. Le premier diagramme a trois parts violettes et cinq parts
blanches. Il indique trois huitièmes. Le deuxième a deux parts violettes et indique deux huitièmes. Une flèche le
relie au suivant. Le troisième a cinq parts violettes et indique cinq huitièmes. Et le quatrième est tout blanc et
n’indique aucune fraction.
Les élèves progressent vers des problèmes comportant des fractions avec dénominateurs différents. Les élèves peuvent néanmoins explorer ce type de problème dans un contexte à l’aide de représentations concrètes et semi-concrètes.
Par exemple, Alexis et son frère Mycolas ont chacun une barre tendre. Les barres sont identiques. Alexis a mangé le tiers (\(\frac{1}{3}\)) de sa barre tendre et Mycolas a mangé les 3 quarts (\(\frac{3}{4}\)) de la sienne. Quelle quantité de barres tendres leur reste-t-il en tout ?
Cette situation représente certes un défi pour les élèves, mais si elles et s’ils ont recours à des repères, à une visualisation de la situation ou à une représentation semi-concrète, elles et ils sont en mesure de conclure qu’il reste presque une barre tendre au complet.
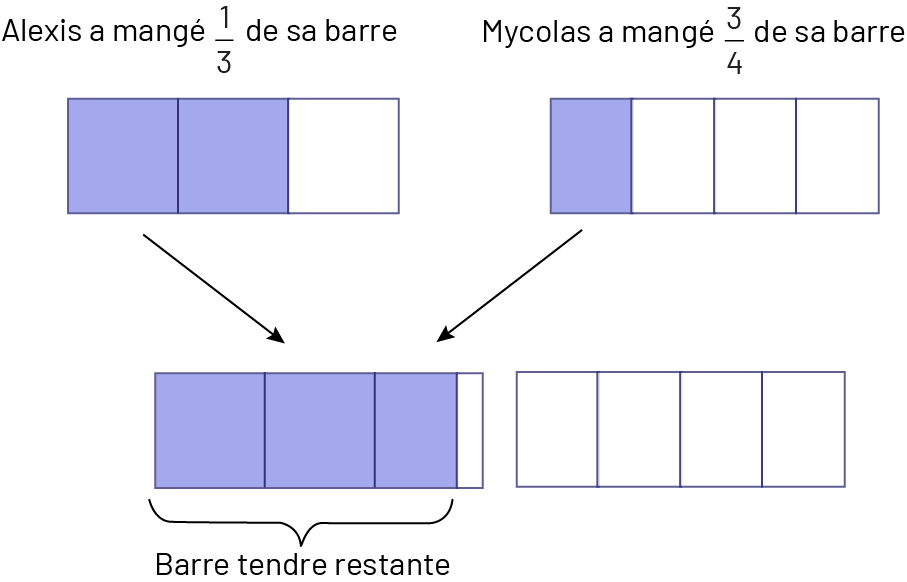 Image L’image montre quatre rectangles de longueur égale. Le premier rectangle est divisé en trois parts égales,
deux des trois parts sont colorées en violet et la troisième part est blanche. Au-dessus, il est écrit : Alexis a
mangé un tiers de sa barre. Le deuxième rectangle est divisé en quatre parts égales, l’une d’elles est colorée en
violet et les autres sont
blanches. Au-dessus, il est écrit : Mycolas a mangé trois-quarts de sa barre. Le troisième rectangle est divisé en
trois parts égales. Deux parts sont colorées en violet et les trois quarts de
la dernière part sont violets, tandis que le reste est blanc. Une accolade en dessous indique « barre tendre
restante ». Le quatrième rectangle est divisé en quatre parts blanches égales.
Image L’image montre quatre rectangles de longueur égale. Le premier rectangle est divisé en trois parts égales,
deux des trois parts sont colorées en violet et la troisième part est blanche. Au-dessus, il est écrit : Alexis a
mangé un tiers de sa barre. Le deuxième rectangle est divisé en quatre parts égales, l’une d’elles est colorée en
violet et les autres sont
blanches. Au-dessus, il est écrit : Mycolas a mangé trois-quarts de sa barre. Le troisième rectangle est divisé en
trois parts égales. Deux parts sont colorées en violet et les trois quarts de
la dernière part sont violets, tandis que le reste est blanc. Une accolade en dessous indique « barre tendre
restante ». Le quatrième rectangle est divisé en quatre parts blanches égales.
Cette situation est représentée à l’aide d’un modèle de surface. La forme rectangulaire est plutôt naturelle, puisqu’elle ressemble à une barre tendre. Cependant, il ne faut pas négliger d’autres représentations, comme le modèle de longueur.
L’exemple suivant porte sur la distance et fait appel aux nombres fractionnaires :
Dans le cadre d’un entraînement pour une course, William doit parcourir au moins \(6\frac{1}{{10}}\) km par jour. Ce matin, avant d’aller à l’école, il a couru \(3\frac{3}{{10}}\) km. Combien de kilomètres doit-il parcourir après l’école?
Puisque la situation traite d’une mesure linéaire, les élèves peuvent avoir recours à un modèle de longueur tel que la droite numérique. Il s’agit d’abord de situer \(6\frac{1}{{10}}\) sur une droite numérique graduée (à gauche) ou une droite numérique non graduée (à droite),
 Image Deux droites numériques sont placées côte à côte. La première
droite est graduée de zéro à sept par intervalles d’un, avec des marques d’intervalles d’un dixième. Une flèche part
de zéro et se rend à six. La deuxième droite est graduée de zéro à six et un dixième et ne présente aucune marque
d’intervalle.
Image Deux droites numériques sont placées côte à côte. La première
droite est graduée de zéro à sept par intervalles d’un, avec des marques d’intervalles d’un dixième. Une flèche part
de zéro et se rend à six. La deuxième droite est graduée de zéro à six et un dixième et ne présente aucune marque
d’intervalle.
ensuite de soustraire 3 de \(6\frac{1}{10}\)
 Image Deux droites numériques sont placées côte à côte. La première
droite est graduée de zéro à sept par intervalles d’un, avec des marques d’intervalles d’un dixième. Une flèche part
de zéro et se rend à six. La deuxième droite est graduée de zéro à six et un dixième et ne présente aucune marque
d’intervalle.
Image Deux droites numériques sont placées côte à côte. La première
droite est graduée de zéro à sept par intervalles d’un, avec des marques d’intervalles d’un dixième. Une flèche part
de zéro et se rend à six. La deuxième droite est graduée de zéro à six et un dixième et ne présente aucune marque
d’intervalle.
puis de soustraire la partie fractionnaire, soit \(\frac{3}{{10}}\) ou 3 fois \(\frac{1}{{10}}\).
 Image
Deux droites numériques sont placées côte à côte. La première droite est graduée de zéro à sept par intervalles d’un,
avec des marques d’intervalles d’un dixième. Une flèche part de trois et un dixième et recule à deux et huit dixièmes
en indiquant moins trois dixièmes. La deuxième droite est graduée de zéro à six et un dixième et ne présente aucune
marque d’intervalle, mais elle affiche les chiffres deux et huit dixième ainsi que trois et un dixième. Une flèche
part de ce dernier chiffre et recule à deux et huit dixièmes en indiquant moins trois dixièmes.
Image
Deux droites numériques sont placées côte à côte. La première droite est graduée de zéro à sept par intervalles d’un,
avec des marques d’intervalles d’un dixième. Une flèche part de trois et un dixième et recule à deux et huit dixièmes
en indiquant moins trois dixièmes. La deuxième droite est graduée de zéro à six et un dixième et ne présente aucune
marque d’intervalle, mais elle affiche les chiffres deux et huit dixième ainsi que trois et un dixième. Une flèche
part de ce dernier chiffre et recule à deux et huit dixièmes en indiquant moins trois dixièmes.
Ainsi, on peut conclure que William doit parcourir \(2\frac{8}{{10}}\) km. On a donc \(6\frac{1}{{10}}\; - \;3\frac{3}{{10}}\; = \;2\frac{8}{{10}}\).
Bien que le modèle de longueur représente fidèlement la situation, les élèves pourraient représenter l’opération en utilisant un modèle de surface comme illustré ci-dessous.
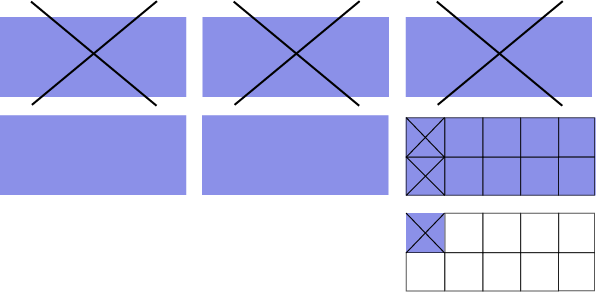 Image
Sept rectangles sont présentés en deux rangée de trois et une rangée d’un. Les trois du haut sont violets et barrés
d’un « X ». Les deux premiers de la deuxième rangée sont complètement violets et entiers. Le troisième de la deuxième
rangée est violet et divisé en deux rangées de cinq cases. Les premières cases du haut et du bas sont marquées d’un «
X ». Le septième rectangle est divisé en deux rangées de cinq cases. La première est violette et marquée d’un « X »
tandis que les autres sont blanches et intactes.
Image
Sept rectangles sont présentés en deux rangée de trois et une rangée d’un. Les trois du haut sont violets et barrés
d’un « X ». Les deux premiers de la deuxième rangée sont complètement violets et entiers. Le troisième de la deuxième
rangée est violet et divisé en deux rangées de cinq cases. Les premières cases du haut et du bas sont marquées d’un «
X ». Le septième rectangle est divisé en deux rangées de cinq cases. La première est violette et marquée d’un « X »
tandis que les autres sont blanches et intactes.
Cette situation peut aussi être résolue en décomposant \(6\frac{1}{{10}}\) en \(5\; + \;\frac{{10}}{{10}}\) pour ensuite combiner les fractions, donc \(5\; + \;\frac{{10}}{{10}}\; + \;\frac{1}{{10}}\; = \;5\frac{{11}}{{10}}\).
Maintenant, on peut soustraire \(5\frac{{11}}{{10}}\; - \;3\frac{3}{{10}}\; = \;2\frac{8}{{10}}\).
Les élèves doivent aussi explorer des situations comprenant des fractions impropres. Par exemple, l’opération \(\frac{{10}}{4}\; + \;\frac{3}{4}\) pourrait être représentée à l’aide du modèle suivant.
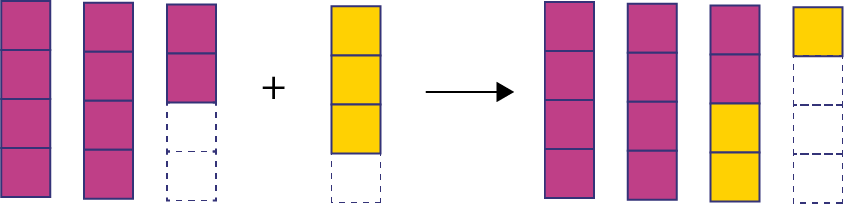 Image
Quatre colonnes de quatre carrés sont placées côte à côte. Les deux premières sont complètement fuchsia. La troisième
possède deux carrés fuchsia et deux blancs. Un symbole plus précède la quatrième colonne, qui possède trois carrés
fuchsia et un blanc. Une flèche pointe vers la prochaine colonne, qui comme la suivante est complètement fuchsia. La
septième colonne a deux carrés fuchsia et deux carrés orange. La huitième colonne a un carré orange et trois carrés
blancs.
Image
Quatre colonnes de quatre carrés sont placées côte à côte. Les deux premières sont complètement fuchsia. La troisième
possède deux carrés fuchsia et deux blancs. Un symbole plus précède la quatrième colonne, qui possède trois carrés
fuchsia et un blanc. Une flèche pointe vers la prochaine colonne, qui comme la suivante est complètement fuchsia. La
septième colonne a deux carrés fuchsia et deux carrés orange. La huitième colonne a un carré orange et trois carrés
blancs.
Ce modèle permet d’exprimer le résultat sous la forme \(\frac{{13}}{4}\), si on compte les quarts, ou \(3\frac{1}{4}\), si on tient compte des touts.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 92-94.
Voici différents types de problèmes relatifs à l’addition et à la soustraction (problèmes d’ajout, problèmes de retrait, problèmes de comparaison et problèmes de réunion).
Exemples
Problèmes d’ajout
Mila a mangé \(\frac{2}{8}\) d’un sous-marin, alors que Pierre en a mangé \(\frac{1}{2}\). Quelle fraction du sous-marin a été mangée par les 2 enfants?
\(\frac{2}{8}\; + \;\frac{1}{2}\; = \;?\)
Représentation à l’aide de bandes fractionnaires
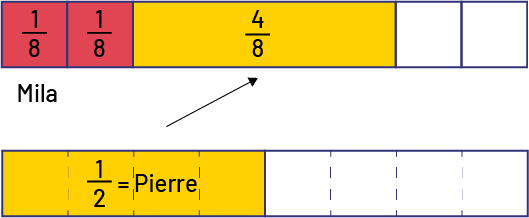 Image Deux rectangles de longueur égale sont placés l’un sous l’autre. Le premier rectangle est divisé en cinq parts.
Les deux premières sont rouges, d‘égale longueur, et indiquent un
huitième. La troisième est plus longue, jaune, et indique quatre huitièmes. Les deux dernières sont blanches, de
longueur égale et équivalent aux deux premières. Le nom Mila est écrit sous la première part. Le deuxième rectangle
est divisé en huit parts égales. Les quatre premières sont jaunes, et sur celles-ci, il est
écrit : un demi égale Pierre. Une flèche part de celles-ci et pointe vers la part jaune à quatre huitièmes du
rectangle au-dessus. Les quatre autres parts du deuxième rectangle sont blanches.
Image Deux rectangles de longueur égale sont placés l’un sous l’autre. Le premier rectangle est divisé en cinq parts.
Les deux premières sont rouges, d‘égale longueur, et indiquent un
huitième. La troisième est plus longue, jaune, et indique quatre huitièmes. Les deux dernières sont blanches, de
longueur égale et équivalent aux deux premières. Le nom Mila est écrit sous la première part. Le deuxième rectangle
est divisé en huit parts égales. Les quatre premières sont jaunes, et sur celles-ci, il est
écrit : un demi égale Pierre. Une flèche part de celles-ci et pointe vers la part jaune à quatre huitièmes du
rectangle au-dessus. Les quatre autres parts du deuxième rectangle sont blanches.
\(\begin{align}\frac{2}{8}\; + \;\frac{1}{2}\; &= \;\frac{2}{8}\; + \frac{4}{8}\; \\ &= \frac{6}{8}\; \\ &= \;\frac{3}{4}\end{align}\)
\(\frac{6}{8}\;\;{\rm{ou}}\;\;\frac{3}{4}\)du sous-marin a été mangée par les 2 enfants.
Source : Problème modifié de Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
La fourmi rouge mesure \(\frac{3}{{10}}\) de centimètre, la cigale mesure \(1\frac{1}{5}\) de centimètre, le scarabée mesure \(\frac{2}{{10}}\) de centimètre et la coccinelle mesure \(\frac{3}{{10}}\) de centimètre;
- Quelle fraction impropre représente la longueur en centimètres de la suite d’insectes?
- Quelle est cette longueur en mètres?
Pour additionner les fractions, il faut les représenter à l’aide d’un dénominateur commun. Alors, pour la longueur de la cigale, je trouve une fraction équivalente qui a le même dénominateur que les autres fractions.
 Image
Une droite numérique est graduée de zéro à deux mètres, avec intervalle d’un mètre et avec marques d’intervalles de
zéro virgule un. Une flèche relie zéro à un virgule deux en indiquant douze dixièmes. Une flèche relie un virgule deux
à un virgule cinq en indiquant trois dixièmes. Une flèche relie un virgule cinq à un virgule sept en indiquant deux
dixièmes. Et une flèche relie un virgule sept à deux en indiquant trois dixièmes.
Image
Une droite numérique est graduée de zéro à deux mètres, avec intervalle d’un mètre et avec marques d’intervalles de
zéro virgule un. Une flèche relie zéro à un virgule deux en indiquant douze dixièmes. Une flèche relie un virgule deux
à un virgule cinq en indiquant trois dixièmes. Une flèche relie un virgule cinq à un virgule sept en indiquant deux
dixièmes. Et une flèche relie un virgule sept à deux en indiquant trois dixièmes.
Sa longueur est \(\frac{{20}}{{10}}\) de centimètres ou 2 cm. Sa longueur en mètres est \(\frac{2}{100}\) de mètre ou 0,02 m.
Source : adapté de L'@telier - Ressources pédagogiques en ligne (atelier.on.ca)
Problème de comparaison
Mila a pris \(\frac{1}{4}\) d’un pichet d’eau pour arroser sa plante. Pierre a pris \(\frac{5}{8}\) du pichet pour arroser la sienne. Quelle fraction représente la différence entre les quantités d’eau utilisées par Pierre et Mila?
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
Pour soustraire les fractions, il faut les représenter à l’aide d’un dénominateur commun. Alors, pour la quantité d’eau de Mila, je trouve la fraction équivalente qui a le même dénominateur que l’autre fraction. Je sais que \(\frac{1}{4}\; = \;\frac{2}{8}\) puisque 8 est un multiple de 4. Je multiplie le dénominateur par 2 pour avoir des huitièmes, alors je multiplie le numérateur par 2 aussi, pour avoir \(\frac{2}{8}\).
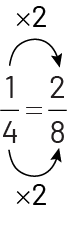
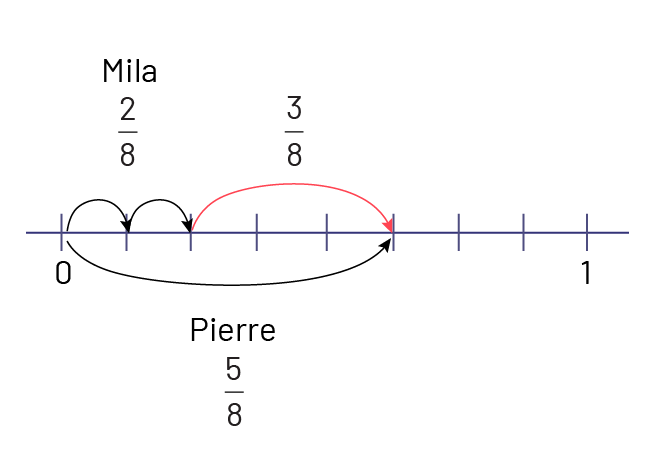 Image Une droite numérique est graduée de zéro à un avec des
marques d’intervalles d’un huitième. Deux flèches noires bondissent de zéro à un huitième et d’un huitième à deux
huitièmes. Au-dessus, il est écrit Mila deux huitièmes. Une flèche rouge bondit de deux huitièmes à cinq huitièmes,
et une flèche noire bondit de zéro à cinq huitièmes. Sous cette dernière, il est écrit Pierre cinq huitièmes.
Image Une droite numérique est graduée de zéro à un avec des
marques d’intervalles d’un huitième. Deux flèches noires bondissent de zéro à un huitième et d’un huitième à deux
huitièmes. Au-dessus, il est écrit Mila deux huitièmes. Une flèche rouge bondit de deux huitièmes à cinq huitièmes,
et une flèche noire bondit de zéro à cinq huitièmes. Sous cette dernière, il est écrit Pierre cinq huitièmes.
Il y a une différence de \(\frac{3}{8}\) d’eau du pichet.
Calcul mental
Dans la vie quotidienne, les élèves font souvent face à des situations impliquant des opérations sur les fractions, par exemple, les soldes d’un magasin lorsque les articles sont offerts à moitié prix, ou la manchette du journal qui indique que le nombre d’inscriptions dans un programme collégial a augmenté de un tiers. Dans de telles situations, il faut souvent effectuer un calcul mental. Selon le contexte, on cherche soit une estimation, soit une réponse exacte.
Un calcul mental repose sur l’utilisation des relations entre les nombres et entre les opérations. Il exige une certaine flexibilité de raisonnement en ce qui a trait aux calculs à effectuer. Au cours d’un calcul mental, les nombres sont souvent décomposés (par exemple, \(\frac{3}{4}\; = \;\frac{2}{4}\; + \;\frac{1}{4}\) ou \(\frac{1}{2}\; + \;\frac{1}{4}\)) et les opérations sont interprétées ou modifiées (par exemple, \(\frac{1}{2}\; + \;\frac{3}{4}\; = \;1\frac{1}{2}\)) sachant que les 3 quarts sont composés de 1 demi et de 1 quart, les 2 demis sont combinés pour faire un tout, puis 1 quart est ajouté.
Exemple
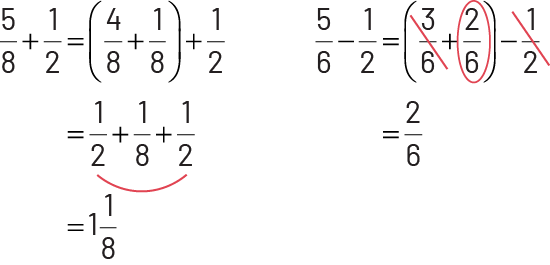 Image Deux longues séquences sont présentées l’une sous l’autre. Première séquence : cinq huitièmes plus un demi
égale parenthèse ouvrante quatre huitièmes plus un huitième
parenthèse fermante plus un demi égale un demi plus un huitième plus un demi égale un et un huitième. Un trait rouge
courbé relie l’avant-dernier un demi au dernier un demi. Deuxième séquence : cinq sixièmes moins un demi égale
parenthèse ouvrante trois sixièmes plus deux sixièmes
parenthèse fermante moins un demi égale deux sixièmes. Trois sixièmes est barré par un trait rouge, le premier deux
sixièmes est encerclé, et le dernier un demi est
barré.
Image Deux longues séquences sont présentées l’une sous l’autre. Première séquence : cinq huitièmes plus un demi
égale parenthèse ouvrante quatre huitièmes plus un huitième
parenthèse fermante plus un demi égale un demi plus un huitième plus un demi égale un et un huitième. Un trait rouge
courbé relie l’avant-dernier un demi au dernier un demi. Deuxième séquence : cinq sixièmes moins un demi égale
parenthèse ouvrante trois sixièmes plus deux sixièmes
parenthèse fermante moins un demi égale deux sixièmes. Trois sixièmes est barré par un trait rouge, le premier deux
sixièmes est encerclé, et le dernier un demi est
barré.
Je sais que \(\frac{3}{6}\) est égal à \(\frac{1}{2}\), alors je décompose \(\frac{5}{6}\) en \(\frac{3}{6}\; + \;\frac{2}{6}\). J’élimine les deux\(\frac{1}{2}\). Il me reste \(\frac{2}{6}\).
La fraction \(\frac{2}{6}\) peut être réduite à \(\frac{1}{3}\).
Il est évident que pour pouvoir effectuer mentalement une opération avec des fractions, les élèves doivent avoir une bonne compréhension des fractions, des opérations et des opérations sur les fractions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 87.
Connaissance : dénominateur
Nombre de parties équivalentes du tout dont se compose la fraction.
Par exemple, le tout est une longueur.
\(\frac{2}{3}\) du segment est rouge.
Le dénominateur « 3 » de la fraction \(\frac{2}{3}\), représente les 3 parties équivalentes sectionnées de la droite numérique.
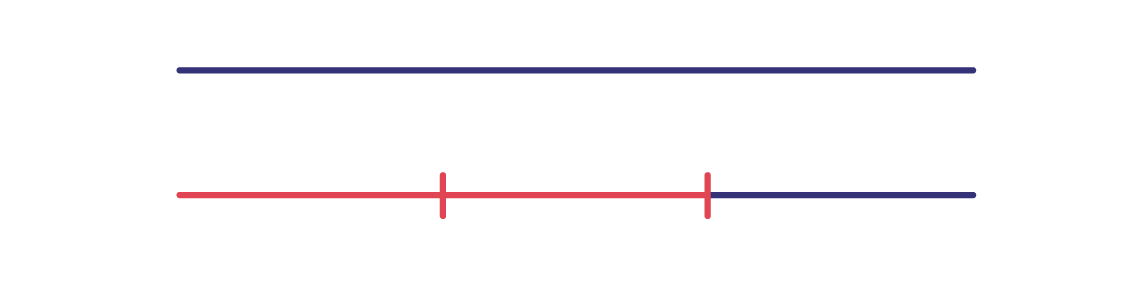 Image Deux lignes de la même longueur sont placées l’une sous l’autre.
La première est toute noire, tandis que la deuxième est séparée en trois parties égales. Les deux premières sont
rouges et la deuxième est noire.
Image Deux lignes de la même longueur sont placées l’une sous l’autre.
La première est toute noire, tandis que la deuxième est séparée en trois parties égales. Les deux premières sont
rouges et la deuxième est noire.
Connaissance : numérateur
Nombre de parties équivalentes par lequel le tout est divisé.
Par exemple, le tout est une longueur.
\(\frac{2}{3}\) du segment est rouge.
Le numérateur « 2 » de la fraction \(\frac{2}{3}\), représente les 2 parties rouges des 3 sections équivalentes de la droite numérique.
 Image Deux lignes de la même longueur sont placées l’une sous
l’autre. La première est toute noire, tandis que la deuxième est séparée en trois parties égales. Les deux premières
sont rouges et la deuxième est noire.
Image Deux lignes de la même longueur sont placées l’une sous
l’autre. La première est toute noire, tandis que la deuxième est séparée en trois parties égales. Les deux premières
sont rouges et la deuxième est noire.
Connaissance : fractions équivalentes
Reconnaître l’égalité de 2 fractions, c’est reconnaître que les 2 fractions représentent la même quantité. Selon Van De Walle et Folk (2005, p. 236 et 237), il faut faire la distinction entre le concept de fractions équivalentes et l’algorithme qui permet de déterminer des fractions équivalentes.
Concept : 2 fractions sont équivalentes si elles représentent la même quantité.
Algorithme : Pour obtenir une fraction équivalente à une fraction quelconque, il faut multiplier ou diviser son numérateur et son dénominateur par le même nombre (différent de 0).
Déterminer des fractions équivalentes, c’est déterminer des fractions qui représentent la même quantité. On cherche alors un nombre de « petites parties » d’un tout qui correspondent à un nombre particulier de « grandes parties » du même tout. Par exemple, si on cherche le nombre de seizièmes qui correspond à un quart (\(\frac{1}{4}\; = \;\frac{?}{{16}}\)) :
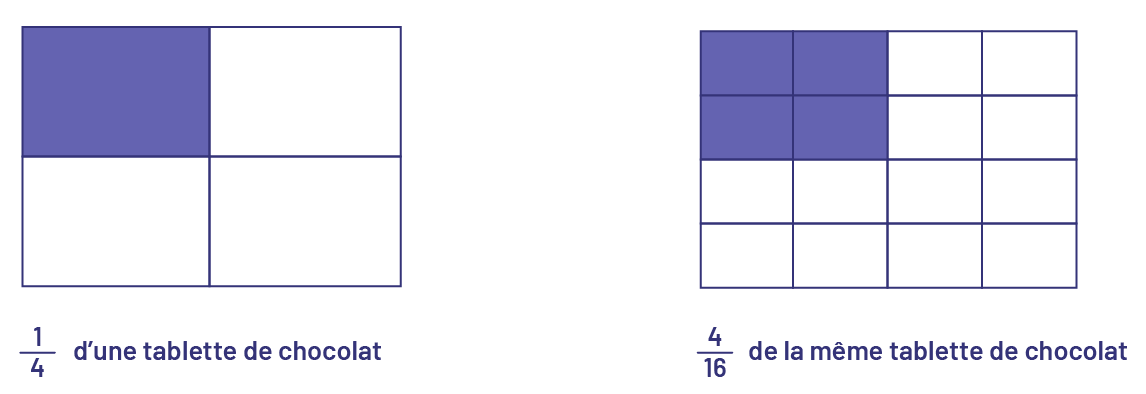 Image Le premier rectangle est divisé en deux rangées de deux
rectangles de taille égale. Le rectangle du coin en
haut à gauche est violet tandis que les trois autres sont blancs. En dessous, il est écrit : Un quart d’une tablette
de chocolat. Le deuxième rectangle est divisé en quatre rangées de quatre rectangles de taille égale. Les quatre
rectangles du
coin en haut à gauche sont violets tandis que les 12 autres sont blancs. En dessous, il est écrit : Quatre seizièmes
de la même tablette de chocolat.
Image Le premier rectangle est divisé en deux rangées de deux
rectangles de taille égale. Le rectangle du coin en
haut à gauche est violet tandis que les trois autres sont blancs. En dessous, il est écrit : Un quart d’une tablette
de chocolat. Le deuxième rectangle est divisé en quatre rangées de quatre rectangles de taille égale. Les quatre
rectangles du
coin en haut à gauche sont violets tandis que les 12 autres sont blancs. En dessous, il est écrit : Quatre seizièmes
de la même tablette de chocolat.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-51.
