B2.5 Add and subtract fractions, using appropriate strategies, in various contexts.
Skill: Adding and Subtracting Fractions in Various Contexts
Make Connections Between Operations on Whole Numbers and Operations on Fractions
Students have already developed a solid understanding of addition and subtraction. It is important to make connections between operations on whole numbers and operations on fractions. For example, adding 3 eighths and 2 eighths is the same as adding 3 candies and 2 candies. Only the notation is different and more complex.
Valuing Informal Procedures to Develop Strategies
It is important to value informal procedures, as they contribute to the development of number sense and operational sense. In situations that involve operations, many students use personal algorithms rather than procedures. For example, a student with good number sense could tackle the addition of \(\frac{7}{8}\) from a sandwich and \(\frac{4}{8}\) from another identical sandwich in this way: "I know that with \(\frac{7}{8}\) of a sandwich, I am missing \(\frac{1}{8}\) of a sandwich to have a complete sandwich. So if I add \(\frac{1}{8}\) to \(\frac{7}{8}\), I have a whole and I'm left with \(\frac{3}{8 }\). So, \(\frac{7}{8}\; + \;\frac{4}{8}\; = \;1\frac{3}{8}\). »
Fundamental Operations
Applying an operation on numbers has the effect of rearranging the quantities involved. It is very important that students understand this aspect of quantity when using any of the four operations. Junior students have had the opportunity to learn this relationship in relation to the four operations on whole numbers. In addition, two quantities are put together to form a new quantity. In subtraction, one quantity is taken away from another. We can also recognize that we are looking for a quantity by which two given quantities differ.
It takes a long time to build a sense of operations on fractions, as one must think about the numerators, denominators, and wholes involved. Students should be given the opportunity to work with concrete and semi-concrete models and develop a sense of the order of magnitude of results before moving on to operations involving symbolic representations.
According to the curriculum,6th graders see addition and subtraction of fractions with like and unlike denominators.
For addition and subtraction with like denominators, it is essentially the addition and subtraction of objects or quantities of the same kind.
For example, in \(\frac{3}{7}\; + \frac{2}{7}\; = \frac{5}{7}\), the addition simply represents 3 one-seventh + 2 one-seventh = 5 one-seventh, just as 3 apples + 2 apples = 5 apples. In this example, sevenths are counted in the same way as apples. We have 3 pieces of a certain size and 2 pieces of the same size, which gives 5 pieces of that size.
Adding fractions becomes more complex when the fractions have unlike denominators, since the pieces are not the same size and not the same kind.
Subtraction is treated the same way. For example, if I take 3 marbles out of a bag that contains 5 marbles, 2 marbles remain. Similarly, if I subtract 3 one-eighths from 5 one-eighths, I have 2 one-eighths left \(\frac{5}{8}\; - \frac{3}{8}\; = \frac{2}{8}\).
Adding two whole numbers increases both initial quantities, while subtracting two whole numbers decreases the initial quantity. It is important for students to understand that the same is true for adding and subtracting fractions.
This allows them to evaluate the reasonableness of some answers obtained from incorrect procedures. For example, a student who adds the numerators and denominators of \(\frac{2}{3}\; + \;\frac{1}{3}\) to obtain \(\frac{3}{6}\) should see that this answer, which is equal to \(\frac{1}{2}\), is less than one of the original fractions, \(\frac{2}{3}\).
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 75-77.
Explore Operations Using Multiple Models
It is important for students to learn fraction-related concepts in a variety of situations using a variety of models such as area models, linear models, and set models. The same is true for learning operations on fractions.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 76.
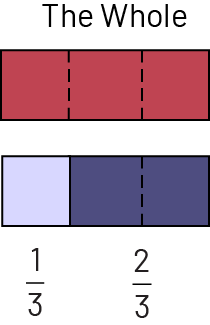
When working with fractions, the most important and sometimes the most difficult thing is to represent the whole correctly. With concrete or semi-concrete material, the visual effect of addition and subtraction is enhanced. Drawing on their experiences with whole numbers and developing a sense of operation, students may recognize, for example, that adding two-thirds (\(\frac{2}{3}\)) to one-third (\(\frac{1}{3}\)] is three-thirds (\(\frac{3}{3}\)), or the whole.
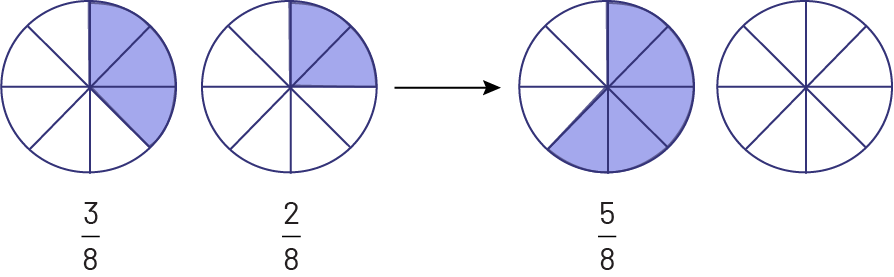
However, it is not always clear to students that addition is in relation to the numerator. In a situation where there are three eighths left of a pizza and two eighths left of another pizza of the same size, we look at how many are left in total. Are we counting eighths or sixteenths, since the pizzas had sixteen pieces in all?
Students progress to problems involving fractions with unlike denominators. Students can explore this type of problem in context using concrete and semi-concrete representations.
For example, Alexis and his brother Mycolas each have a granola bar. The bars are identical. Alexis ate one-third (\(\frac{1}{3}\)) of her granola bar and Mycolas ate three-quarters (\(\frac{3}{4}\)) of his. How many granola bars do they have left altogether?
While this is a challenging situation for students, if they use benchmarks, a visualization of the situation, or a semi-concrete representation, they are able to conclude that there is almost a whole granola bar left.
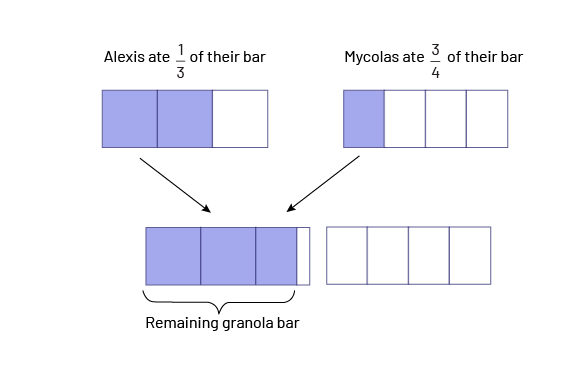
This situation is represented with the help of an area model. The rectangular shape is rather natural, since it looks like a granola bar. However, other representations, such as the linear model, should not be overlooked.
The following example is about distance and uses mixed numbers:
As part of his training for a race, William must run at least \(6\frac{1}{{10}}\) km a day. This morning, before going to school, he ran \(3\frac{3}{{10}}\) km. How many kilometres does he have to run after school?
Since the situation deals with a linear measurement, students can use a linear model such as a number line. The first step is to locate \(6\frac{1}{{10}}\) on a number line (left) or an open number line (right),
then subtract 3 from \(\ 6 \frac{1}{10}\).
then subtract the fractional part, either \(\frac{3}{{10}}\) or 3 times \(\frac{1}{{10}}\).
Thus, we can conclude that William must run \(2\frac{8}{{10}}\) km. We therefore have \(6\frac{1}{{10}}\; - \;3\frac{3}{{10}}\; = \;2\frac{8}{{10}}\).
Although the linear model accurately represents the situation, students could represent the operation using an area model as shown below.
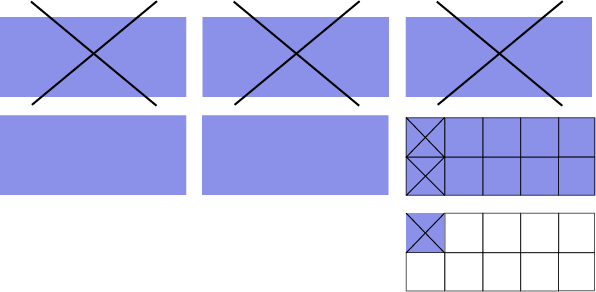
This situation can also be solved by decomposing \(6\frac{1}{{10}}\) into 5 wholes and then combining the fractions, so \(5\; + \;\frac{10}{10}; + \;\frac{1}{10}; = \;5\frac{11}{10}\).
Now we can subtract \(5\frac{{11}}{{10}}\; - \;3\frac{3}{{10}}\; = \;2\frac{8}{{10 }}\).
Students should also explore situations involving improper fractions. For example, the operation \(\frac{{10}}{4}; + \;\frac{3}{4}\) could be represented using the following model.
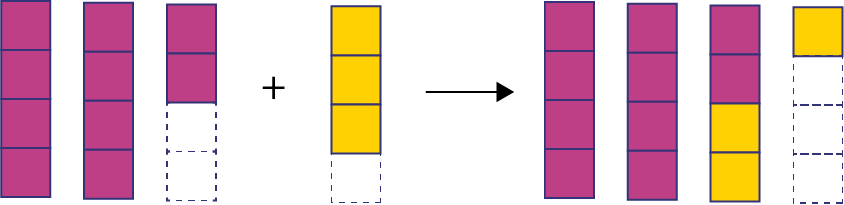
This model allows the result to be expressed as \(\frac{{13}}{4}\), if the fourths are counted, or \(3\frac{1}{4}\), as a mixed number.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 92-94.
Here are different types of problems relating to addition and subtraction (joining problems, separating problems, comparing problems and part-part-whole problems).
Examples
Joining Problems
Mila ate \(\frac{2}{8}\) of a submarine sandwich, while Peter ate \(\frac{1}{2}\). a) What fraction of the submarine sandwich was eaten by the 2 children?
\(\frac{2}{8}\; + \;\frac{1}{2}\; = \;?\)
Representation using fraction strips
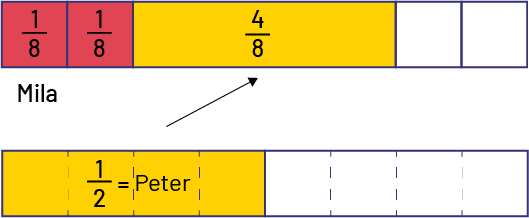
\(\begin{array}{l}\frac{2}{8}\; + \;\frac{1}{2}\; = \;\frac{2}{8}\; + \frac{ 4}{8}\;=\;\frac{6}{8}\\\frac{6}{8}\;=\;\frac{3}{4}\end{array}\)
\(\frac{6}{8}\;{\rm{ou}}\;\frac{3}{4}\)of the submarine was eaten by the 2 children.
Source: Problem modified from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
The red ant is \(\frac{3}{{10}}\) centimetre long, the cicada is \(1\frac{1}{5}\) centimetre long, the beetle is \(\frac{2} {{10}}\) centimetre long and the ladybug is \(\frac{3}{{10}}\) centimetre long.
- Which improper fraction represents the total length in centimetres of the insects?
- What is this length in metres?
To add fractions, you need to represent them using like denominators. So, for the length of the cicada, I find an equivalent fraction that has the same denominator as the other fractions.
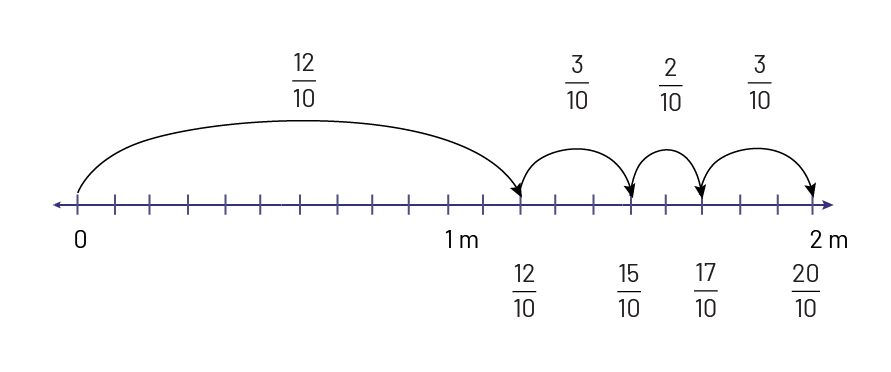
Its length is \(\frac{{20}}{{10}}\) centimetres or 2 cm. Its length in metres is \(\frac{2}{100}\) of metre or 0.02 m.
Source : adapted from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca)
Comparing Problem
Mila took \(\frac{1}{4}\) from a pitcher of water to water her plant. Peter took \(\frac{5}{8}\) from the pitcher to water his own. What fraction represents the difference between the amounts of water used by Peter and Mila?
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
To subtract fractions, you need to represent them using a common denominator. So, for Mila's quantity of water, I find the equivalent fraction that has the same denominator as the other fraction. I know that \(\frac{1}{4}\; = \;\frac{2}{8}\) since 8 is a multiple of 4. I multiply the denominator by 2 to get eighths, so I multiply the numerator by 2 too, to get \(\frac{2}{8}\).
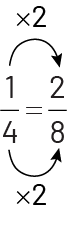
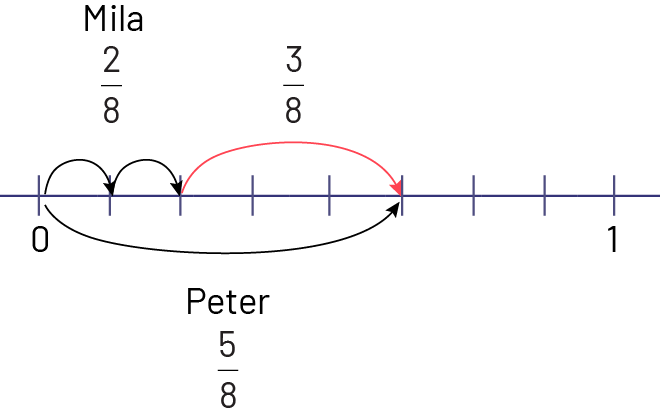
There is a difference of \(\frac{3}{8}\) of water from the pitchers.
Mental Math
In everyday life, students often encounter situations involving fraction operations, such as a store sale when items are offered at half price, or the headline in the newspaper that indicates enrollment in a college program has increased by one-third. In such situations, a mental calculation is often required. Depending on the context, either an estimation or an exact answer is sought.
Mental math is based on the use of relationships between numbers and operations. It requires flexibility in reasoning about the calculations to be performed. In mental math, numbers are often decomposed (for example, \(\frac{3}{4}\; = \;\frac{2}{4}\; + \;\frac{1}{4}\) or \(\frac{1}{2}\; + \;\frac{1}{4}\)) or operations are interpreted or modified
(for example, \(\frac{1}{2}\; + \;\frac{3}{4}\; = \;1\frac{1}{2}\)) knowing that the 3 fourths are composed of 1 half and 1 fourth, the 2 halves are combined to make a whole, then 1 fourth is added.
Example
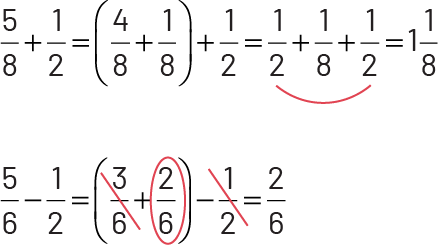
I know that \(\frac{3}{6}\) is equal to \(\frac{1}{2}\), so I decompose \(\frac{5}{6}\) into \(\ frac{3}{6}\;+\;\frac{2}{6}\). I eliminate the \(2\frac{1}{2}\). I still have \(\frac{2}{6}\).
The fraction \(\frac{2}{6}\) can be simplified to \(\frac{1}{3}\).
Clearly, in order to mentally perform an operation with fractions, students must have a good understanding of fractions, operations, and operations with fractions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 87.
Knowledge: Denominator
Number of equal parts into which a whole or set is divided.
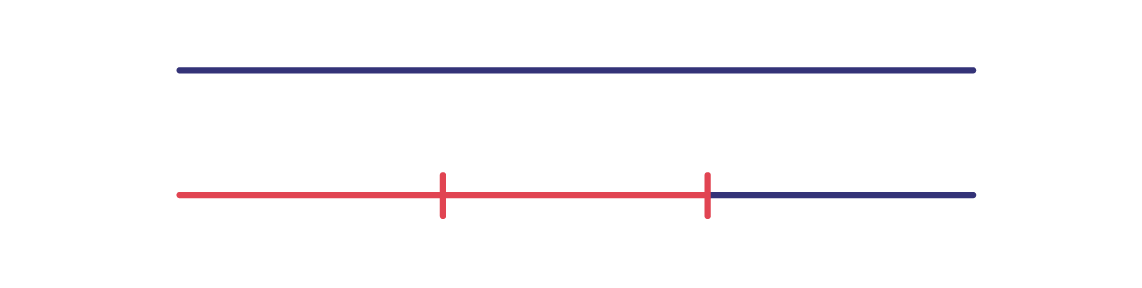
For example, the whole is a length.
\(\frac{2}{3}\) of the segment is red.
The denominator "3" of the fraction \(\frac{2}{3}\), represents the 3 equal parts of the number line.
Knowledge: Numerator
The number above the line in a fraction that represents the number of equal parts being considered.
For example, the whole is a length.
\(\frac{2}{3}\) of the segment is red.
The numerator "2" of the fraction \(\frac{2}{3}\), represents the 2 red parts of the 3 equal sections of the number line.
Knowledge: Equivalent Fractions
To recognize the equality of 2 fractions is to recognize that the 2 fractions represent the same quantity. According to Van de Walle and Folk (2005, pp. 236-237), we must distinguish between the concept of equivalent fractions and the algorithm for determining equivalent fractions.
Concept: Two fractions are equivalent if they represent the same quantity.
Algorithm: To obtain a fraction equivalent to any fraction, multiply or divide its numerator and its denominator by the same number (other than 0).
To determine equivalent fractions is to determine fractions that represent the same quantity. We then seek a number of “small parts” of a whole which correspond to a particular number of “large parts” of the same whole. For example, if we find the number of sixteenths that corresponds to a fourth (\(\frac{1}{4}\; = \;\frac{?}{{16}}\)):
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-51.