B2.6 Multiplier et diviser des fractions par des fractions, des nombres naturels et des nombres fractionnaires, dans divers contextes.
Habileté : multiplier et diviser des fractions par des fractions, des nombres naturels et des nombres fractionnaires, dans divers contextes
Multiplication
Lorsqu’on multiplie des fractions, il y a une certaine progression à suivre. Au cycle moyen, les élèves ont déjà un bagage de connaissances sur la multiplication. En effet, depuis le cycle primaire, elles et ils explorent des concepts reliés à la multiplication à l’aide de matériel concret, de la calculatrice, d’illustrations et de symboles. En 4e année, la multiplication de fractions est limitée à la multiplication d’une fraction unitaire par un nombre naturel. Ce type de multiplication peut être compris en le reliant à l’addition répétée. Ainsi, les élèves saisissent facilement que \(3\; \times \;\frac{1}{2}\), qu’on peut lire « 3 fois un demi », est une multiplication qui peut être représentée par l’addition répétée, soit \(\frac{1}{2}\; + \;\frac{1}{2}\; + \;\frac{1}{2}\). Elles doivent être explorées pour aider les élèves à comprendre la multiplication des fractions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
Exemple
De combien de cartons l’élève qui doit distribuer un demi-carton à quatre camarades aura-t-il besoin?
En comprenant la situation, les élèves reconnaissent qu’il y a multiplication d’une quantité, soit \(4\; \times \;\frac{1}{2}\), qui peut être représentée par une addition répétée, soit \(\frac{1}{2}\; + \;\frac{1}{2}\; + \;\frac{1}{2}\; + \;\frac{1}{2}\). Pour trouver la réponse, les élèves se représentent la situation de façon mentale ou semi-concrète ou utilisent leurs connaissances de l’addition des fractions en question. Certains élèves peuvent visualiser que deux parties égales d’un premier carton sont distribuées à deux camarades et que deux parties égales d’un deuxième carton sont distribuées aux deux autres camarades. Il lui faut donc deux cartons.
D’autres peuvent penser à la représentation abstraite suivante : « Il faut 4 fois un demi-carton. Je sais que \(4\; \times \;\frac{1}{2}\) est égal à 2, car deux demis font 1. Il me faut donc 2 cartons. » D’autres peuvent illustrer le problème comme suit, puis regrouper mentalement les morceaux deux par deux pour constater qu’il y a l’équivalent de deux cartons complets.
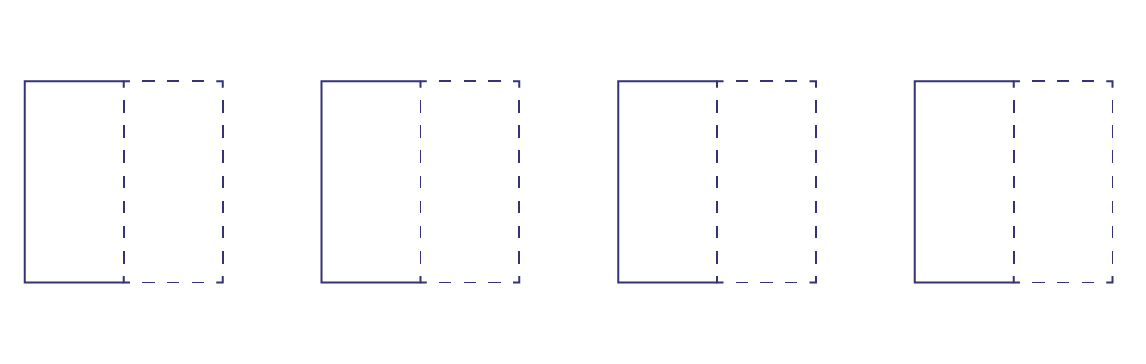
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 86-87.
Multiplication d’un nombre naturel par une fraction
Cependant, il est plus difficile de donner un sens à la multiplication d’un nombre naturel par une fraction (par exemple, \(\frac{1}{2}\; \times \;3\)). Ces situations sont explorées à partir de la 5e année en multipliant un nombre naturel par une fraction unitaire.
Exemple 1
Dans une salle de classe de 8e année, \(\frac{1}{2}\) des élèves portent une tuque.
S’il y a 24 élèves dans la salle de classe, combien d’élèves portent une tuque?
Source : adapté du ministère de l’Éducation de l’Ontario, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 6e année, Module 2, Série 2, Activité 7, p. 281.
- Multiplication effectuée à l’aide d’une droite numérique double
Pour trouver \(\frac{1}{2}\;\;\;{\rm{de}}\;\;\;{\rm{24}}\), je divise 24 par 2, ce qui me donne 12.
Je représente les 24 élèves sous la droite et la moitié de 24 sur le haut de la droite.
 Image
Une droite numérique est graduée de zéro à 26 par marques d’intervalles de deux. Au-dessus, une flèche relie zéro à
douze en indiquant « douze élèves », et en dessous, une flèche relie zéro à 24 en indiquant « 24 élèves ».
Image
Une droite numérique est graduée de zéro à 26 par marques d’intervalles de deux. Au-dessus, une flèche relie zéro à
douze en indiquant « douze élèves », et en dessous, une flèche relie zéro à 24 en indiquant « 24 élèves ».
Il y a 12 élèves qui portent une tuque.
- Multiplication effectuée à l’aide de la disposition rectangulaire
Je décompose 24 en \(20\; + \;4\). Je détermine la moitié de 20 et la moitié de 4, \(10\; + \;2\; = \;12\).
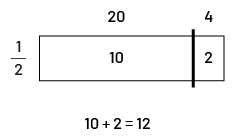 Image
Un rectangle est traversé par une ligne verticale entre le centre et l’extrême droit. Au-dessus du rectangle, il est
écrit le nombre 20 à gauche de la ligne verticale, et le chiffre quatre à droite de la ligne verticale. À l’intérieur
du rectangle, il est écrit dix à gauche de la ligne verticale et deux à droite de la ligne. À gauche du rectangle, il
est écrit un demi.
Image
Un rectangle est traversé par une ligne verticale entre le centre et l’extrême droit. Au-dessus du rectangle, il est
écrit le nombre 20 à gauche de la ligne verticale, et le chiffre quatre à droite de la ligne verticale. À l’intérieur
du rectangle, il est écrit dix à gauche de la ligne verticale et deux à droite de la ligne. À gauche du rectangle, il
est écrit un demi.
Il y a 12 élèves qui portent une tuque.
Exemple 2
Dans un champ de forme rectangulaire dont l’aire est de 100 m2, M. Longpré a semé des concombres sur \(\frac{2}{5}\) de cette surface. Quelle est l’aire du champ, en m2, consacrée à la culture des concombres?
Source : adapté du ministère de l’Éducation de l’Ontario, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 6e année, Module 2, Série 2, Activité 9, Activités à la carte, p. 309.
- Multiplication effectuée à l’aide de la disposition rectangulaire
J’ai décomposé 100 en \(25\; + \;25\; + \;25\; + \;25\). J’ai aussi décomposé \(\frac{2}{5}\) en \(\frac{1}{5}\; + \;\frac{1}{5}\). Je sais que \(\frac{1}{5}\) de 25 est 5 puisque \(5\; \times \;5\; = \;25\).
J’ai additionné les produits partiels pour arriver à 40.
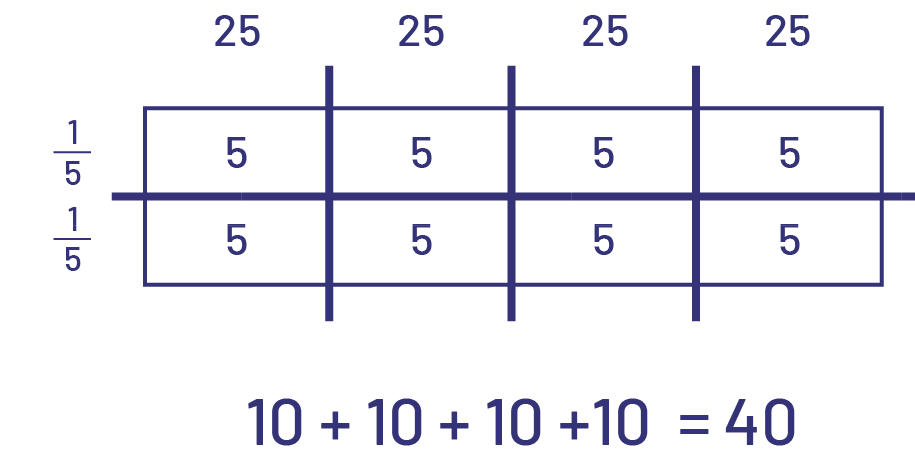 Image Un
rectangle est divisé en huit parts égales, soit deux rangées de quatre parts, lesquelles possèdent chacune le chiffre
cinq. Au-dessus de chaque colonne il est écrit 25, et à gauche de chaque rangée, il est écrit un cinquième. Sous le
rectangle, il est écrit : dix plus dix plus dix plus dix égale 40.
Image Un
rectangle est divisé en huit parts égales, soit deux rangées de quatre parts, lesquelles possèdent chacune le chiffre
cinq. Au-dessus de chaque colonne il est écrit 25, et à gauche de chaque rangée, il est écrit un cinquième. Sous le
rectangle, il est écrit : dix plus dix plus dix plus dix égale 40.
L’aire du champ consacrée à la culture des concombres est 40 m2.
- Multiplication effectuée à l’aide d’un algorithme personnel
J’ai décomposé \(\frac{2}{5}\) en \(2\; \times \;\frac{1}{5}\).
J’ai multiplié \(\frac{1}{5}\; \times \;200\).
Multiplier par \(\frac{1}{5}\) est la même chose que diviser par 5.
J’obtiens 40.
\[\begin{align}\frac{2}{5}\; \times \;100\; = \;2\; \times \;\frac{1}{5}\; \times \;100\; &= \;\frac{1}{5}\; \times \;2\; \times \;100\\\quad \quad \quad \quad \quad \quad \quad \quad \,\; &= \;\frac{1}{5}\; \times 200\\\quad \quad \quad \quad \quad \quad \quad \quad \,\; &= \;200\; \div \;5\\\quad \quad \quad \quad \quad \quad \quad \quad \,\; &= \;40\end{align}\]
L’aire du champ consacrée à la culture des concombres est 40 m2.
Multiplication d’une fraction par une fraction
En 7e année, l’élève multiplie et divise des fractions par d’autres fractions. Ainsi, l’enseignante ou l’enseignant doit amener les élèves à comprendre le sens des opérations et à les représenter visuellement en utilisant diverses représentations.
L’élève qui résout des problèmes utilise du matériel de manipulation et des illustrations pour représenter les fractions et pour simuler l’action qui se dégage de l’énoncé. C’est en partant de ces représentations visuelles qu’elle ou il construit le sens des opérations (×, ÷).
Source : inspiré de Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 8e année, Module 1, Série 2, p. 143-144.
La vidéo suivante montre la multiplication d’une fraction par une fraction à l’aide du modèle de surface, ainsi que l’algorithme représentant la situation.
 Description de la vidéo
Description de la vidéo
Description à venir
Voici d’autres exemples de multiplication de fractions, soient la multiplication sans fractionnement et la multiplication avec fractionnement.
Multiplication sans fractionnement
- Multiplication effectuée à l’aide du modèle de surface
L’élève peut utiliser le modèle de surface, soit le rectangle ou le carré pour multiplier une fraction par une autre fraction.
Exemple
\(\frac{1}{4}\; \times \;\frac{2}{3}\) ou \(\frac{1}{4}\) de \(\frac{2}{3}\)
Puisque je cherche \(\frac{1}{4}\) de \(\frac{2}{3}\), je divise verticalement un rectangle en 3 parties égales et je colorie 2 parties, ce qui correspond à \(\frac{2}{3}\) du rectangle.
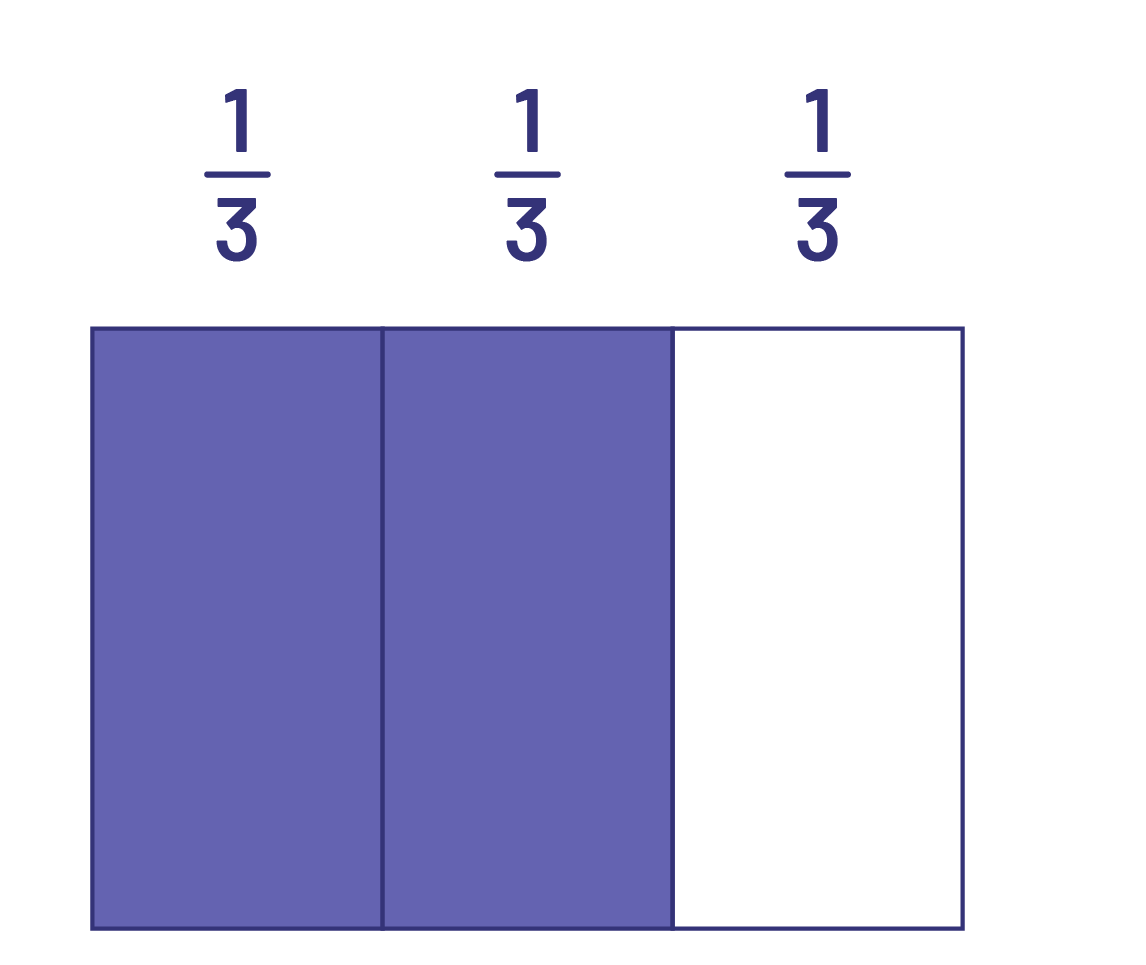 Image Un
rectangle est divisé en trois parties égales sur le sens de la largeur. Les deux premières sont bleues tandis que la
dernière est blanche. Il est écrit un tiers au-dessus de chacune des parties.
Image Un
rectangle est divisé en trois parties égales sur le sens de la largeur. Les deux premières sont bleues tandis que la
dernière est blanche. Il est écrit un tiers au-dessus de chacune des parties.
Ensuite, je divise horizontalement le même rectangle en 4 parties égales et je colorie 1 partie, ce qui correspond à \(\frac{1}{4}\) du rectangle.
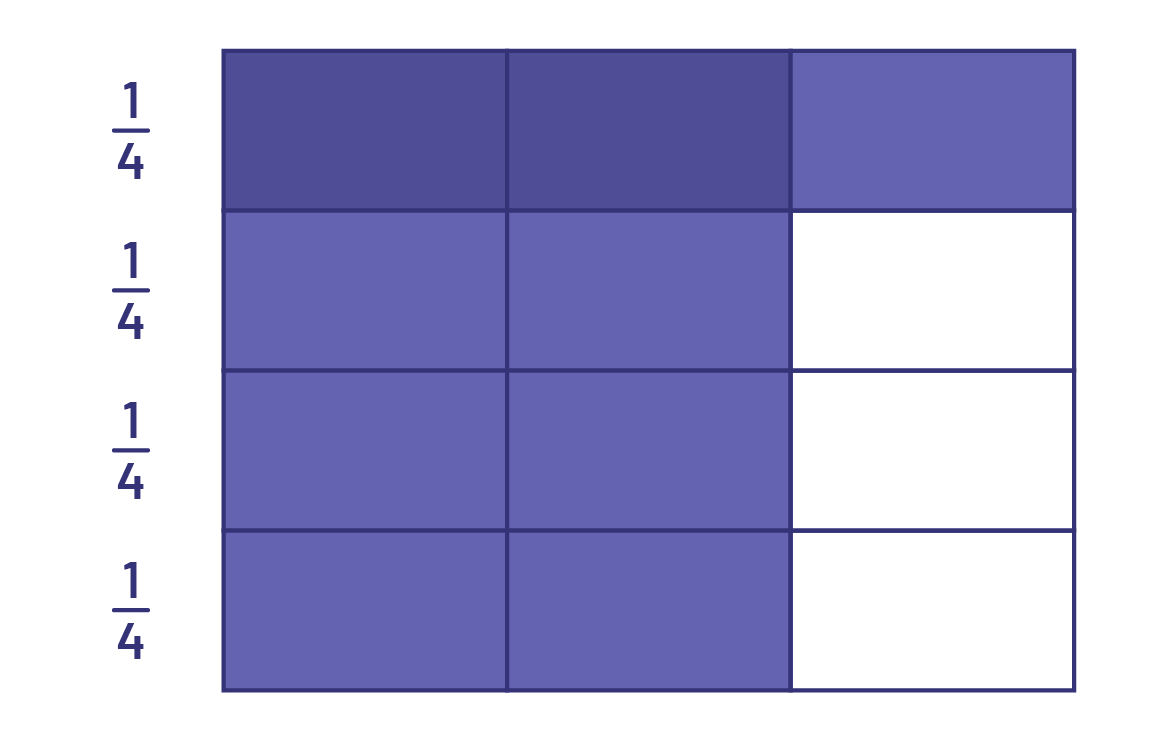 Image Un rectangle est divisé en quatre rangées de trois rectangles
tous égaux. La première rangée a trois rectangles bleus, et les trois autres ont deux rectangles bleus et un blanc. Il
est écrit un quart devant chaque rangée.
Image Un rectangle est divisé en quatre rangées de trois rectangles
tous égaux. La première rangée a trois rectangles bleus, et les trois autres ont deux rectangles bleus et un blanc. Il
est écrit un quart devant chaque rangée.
La fraction qui représente \(\frac{1}{4}\) correspond au nombre de parties coloriées 2 fois, soit \(\frac{2}{{12}}\). Le numérateur correspond aux parties coloriées plus foncées et le dénominateur correspond au nombre de parties de même taille dans le tout, soit 12 parties.
La fraction \(\frac{2}{{12}}\) peut être simplifiée à une fraction équivalente de \(\frac{1}{6}\) en divisant le numérateur et le dénominateur par 2.
- Multiplication effectuée à l’aide d’une représentation symbolique
L’élève multiplie les numérateurs entre eux et les dénominateurs entre eux.
\(\begin{align} \frac{1}{4}\; \times \;\frac{2}{3}\; &= \;\frac{1\; \times \;2}{4\; \times \;3} \\ &= \frac{2}{12} \;\;\; ou \;\;\; \frac{1}{6} \end{align}\)
Source : inspiré de Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 8e année, Module 1, Série 2, p. 253-254.
- Multiplication effectuée en trouvant le PPCM
Le plus petit commun multiple (PPCM) de 4 et 3 est 12.
Je divise un rectangle en 12 parties égales et je représente \(\frac{2}{3}\) du rectangle.
Ensuite, je trouve \(\frac{1}{4}\) de 8 carrés ou \(\frac{1}{4}\) de 2 colonnes = 2 carrés sur 12.
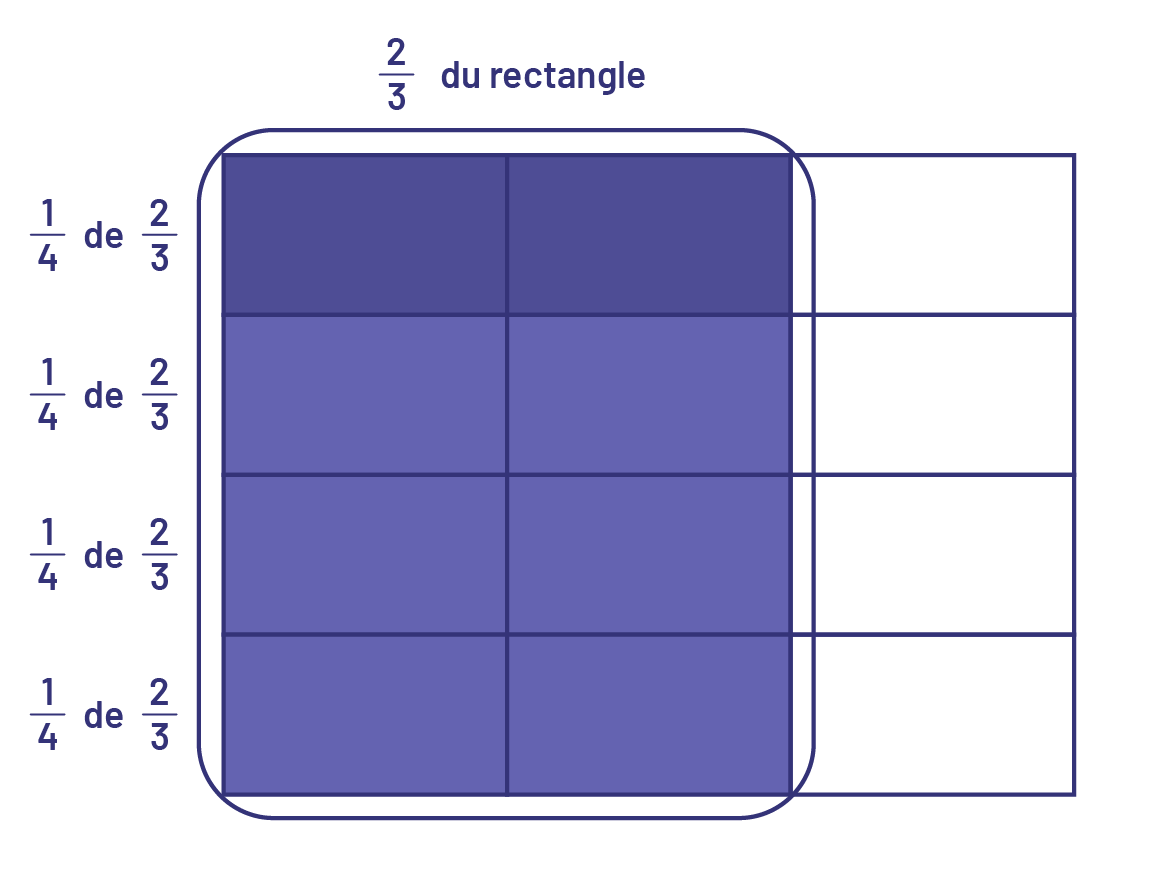 Image Un
rectangle est divisé en quatre rangées de trois rectangles tous égaux. Chaque rangée a deux rectangles bleus et un
blanc. À gauche de chacune d’elle il est écrit un quart de deux tiers. Au-dessus du grand rectangle il est écrit deux
tiers du rectangle.
Image Un
rectangle est divisé en quatre rangées de trois rectangles tous égaux. Chaque rangée a deux rectangles bleus et un
blanc. À gauche de chacune d’elle il est écrit un quart de deux tiers. Au-dessus du grand rectangle il est écrit deux
tiers du rectangle.
Alors, \(\frac{1}{4}\) de \(\frac{2}{3}\) du rectangle est égale à 2 carrés sur l’ensemble des carrés (12).
\(\frac{1}{4}\;\;\;{\rm{de}}\;\;\;\frac{2}{3}\;{\rm{du \;\;\; rectangle}}\; = \frac{2}{{12}}\;\;\;{\rm{ou}}\;\;\;\frac{1}{6}\)
Multiplication avec fractionnement
- Multiplication effectuée à l’aide du modèle de surface
\(\frac{3}{4}\; \times \;\frac{2}{3}\) ou \(\frac{3}{4}\) de \(\frac{2}{3}\)
Puisque je cherche \(\frac{3}{4}\) de \(\frac{2}{3}\), je divise verticalement un rectangle en 3 parties égales et je colorie 2 parties, ce qui correspond à \(\frac{2}{3}\) du rectangle.
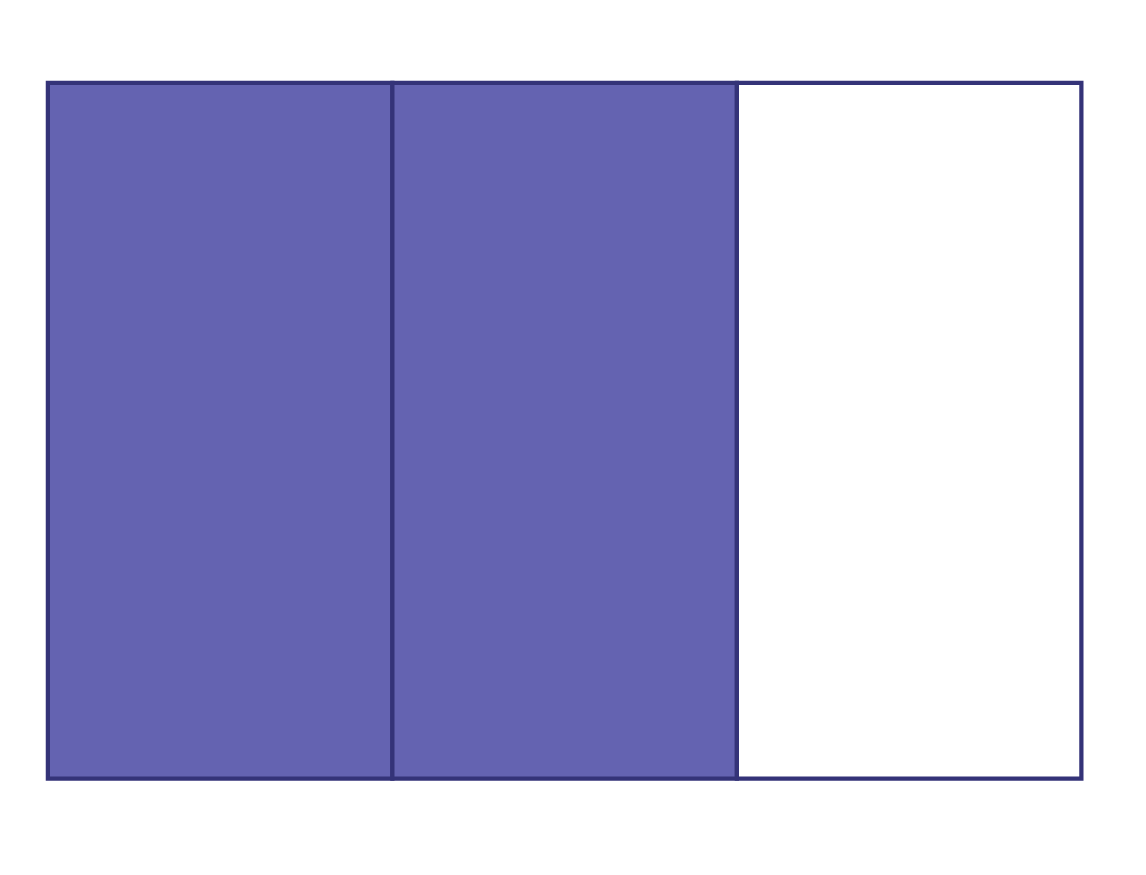
Ensuite, je peux décomposer \(\frac{3}{4}\) en \(\frac{1}{4}\; + \;\frac{1}{4} + \;\frac{1}{4}\).
Je divise horizontalement le même rectangle en 4 parties égales et je colorie tout d’abord 1 partie, ce qui correspond à \(\frac{1}{4}\) du rectangle, soit 3 carrés parmi 12. La fraction qui représente \(\frac{1}{4}\) de \(\frac{2}{3}\) correspond au nombre de parties coloriées 2 fois, soit \(\frac{2}{{12}}\). Le numérateur correspond aux parties coloriées plus foncées et le dénominateur correspond au nombre de parties de même taille dans le tout, soit 12 parties (figure 1).
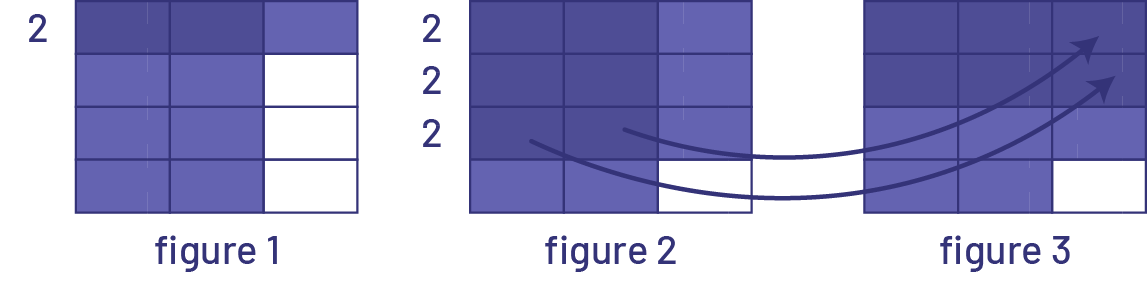 Image La figure un, la figure deux et la figure trois sont placées côte à côte. Ce sont toutes des rectangles
divisés en quatre rangées de trois rectangles tous égaux. La figure un a trois rectangles bleus dans la première
rangée, et les trois autres rangées ont deux rectangles
bleus et un rectangle blanc. Il est écrit « deux » à gauche de la première rangée. La figure deux a des rectangles
bleus partout sauf le dernier en bas à droite. Il est écrit « deux » à gauche des
trois premières rangées. Par des flèches, le premier et le deuxième rectangle de la troisième rangée se lient
respectivement au troisième rectangle de la deuxième rangée et au troisième rectangle de la première rangée de la
figure trois. La figure trois a des rectangles bleus partout sauf le dernier en bas à droite. Il est écrit « deux » à
gauche de
la première rangée.
Image La figure un, la figure deux et la figure trois sont placées côte à côte. Ce sont toutes des rectangles
divisés en quatre rangées de trois rectangles tous égaux. La figure un a trois rectangles bleus dans la première
rangée, et les trois autres rangées ont deux rectangles
bleus et un rectangle blanc. Il est écrit « deux » à gauche de la première rangée. La figure deux a des rectangles
bleus partout sauf le dernier en bas à droite. Il est écrit « deux » à gauche des
trois premières rangées. Par des flèches, le premier et le deuxième rectangle de la troisième rangée se lient
respectivement au troisième rectangle de la deuxième rangée et au troisième rectangle de la première rangée de la
figure trois. La figure trois a des rectangles bleus partout sauf le dernier en bas à droite. Il est écrit « deux » à
gauche de
la première rangée.
Je cherche \(\frac{3}{4}\), alors je peux faire \(2\; + \;2\; + \;2\) puisque \(\frac{1}{4}\) représente 2 carrés. Alors, \(\frac{3}{4}\) représente 6 carrés. \(\frac{3}{4}\) de \(\frac{2}{3}\) représente \(\frac{6}{{12}}\) du tout (figure 2). Si je déplace 2 des carrés (figure 3), je peux voir que \(\frac{6}{{12}}\) est aussi \(\frac{1}{2}\) du tout.
Multiplication d’une fraction par un nombre naturel
En 8e année, les élèves abordent la multiplication de fractions par des nombres naturels (par exemple, \(7\; \times \;\frac{3}{4}\)). Aux cycles primaire et moyen, les élèves ont reconnu le lien entre la multiplication et une addition répétée. Ce lien peut aussi être appliqué dans le cas de multiplications de fractions par des nombres naturels. Or, pour mettre l’accent sur la multiplication comme opération, il est utile de la représenter de diverses façons. Par exemple, l’opération \(4\; \times \;\frac{1}{2}\) qui est lue « quatre fois un demi » peut être représentée par 4 groupes de \(\frac{1}{2}\)(Figure 1) ou à l’aide d’une disposition rectangulaire (Figure 2).
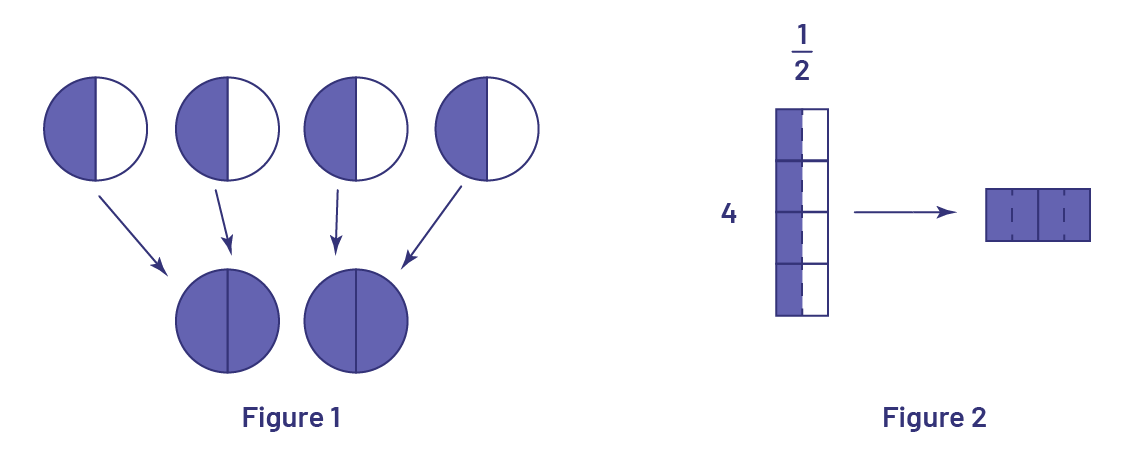 Image Deux illustrations sont présentées : figure un et figure deux. La figure un affiche quatre cercles séparés en
deux parties égales verticalement, la moitié gauche bleue et la
moitié droite blanche. Tous les cercles pointent à l’aide de flèches vers deux cercles en bas, séparés en deux à la
verticale, et présentant deux moitiés bleues. La figure deux montre un rectangle vertical divisé en quatre carrés
égaux. Une ligne verticale divise les quatre
carrés en deux parties égales; le côté gauche est bleu et le côté droit est blanc. À gauche du rectangle il est
écrit quatre, en haut il est écrit un demi. Le rectangle pointe à droite à l’aide d’une flèche vers un rectangle
horizontal divisé en deux parties égales verticalement et présentant deux moitiés bleues.
Image Deux illustrations sont présentées : figure un et figure deux. La figure un affiche quatre cercles séparés en
deux parties égales verticalement, la moitié gauche bleue et la
moitié droite blanche. Tous les cercles pointent à l’aide de flèches vers deux cercles en bas, séparés en deux à la
verticale, et présentant deux moitiés bleues. La figure deux montre un rectangle vertical divisé en quatre carrés
égaux. Une ligne verticale divise les quatre
carrés en deux parties égales; le côté gauche est bleu et le côté droit est blanc. À gauche du rectangle il est
écrit quatre, en haut il est écrit un demi. Le rectangle pointe à droite à l’aide d’une flèche vers un rectangle
horizontal divisé en deux parties égales verticalement et présentant deux moitiés bleues.
Afin d’effectuer une multiplication d’une fraction par un nombre naturel, les élèves développent des stratégies personnelles en utilisant divers modèles. Prenons la situation suivante :
Lors d’une journée d’activités, on veut que les élèves vivent six activités différentes d’une durée de trois quarts d’heure chacune. Quelle sera la durée de l’ensemble des activités?
Pour résoudre ce problème, on peut reconnaître qu’on peut effectuer l’opération \(6\; \times \;\frac{3}{4}\). Afin d’en déterminer le résultat, diverses stratégies de calcul sont possibles telles que :
- effectuer l’addition répétée; \(\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; = \;\frac{{18}}{4}\;\;\;{\rm{donc}}\;\;\;4\frac{2}{4}\;\;\;{\rm{ou}}\;\;\;4\frac{1}{2}\);
- utiliser une représentation concrète;
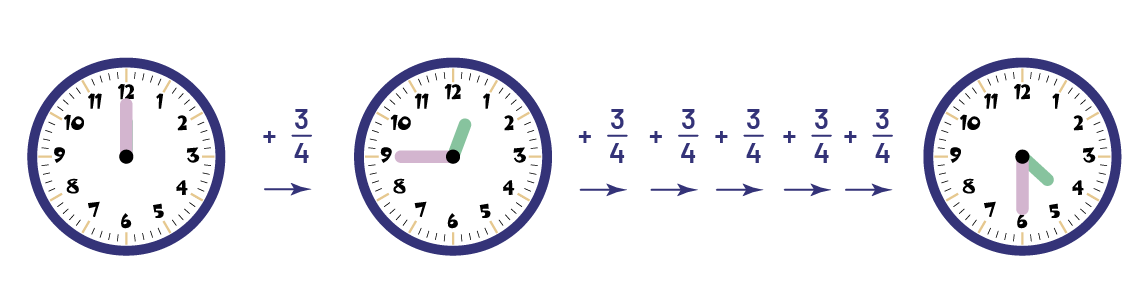 Image L’illustration montre des horloges, des flèches et des fractions toutes alignées côte à côte. La
première horloge affiche douze heures. À sa droite, il est écrit « plus trois quarts » au-dessus d’une flèche qui
pointe à droite vers la prochaine horloge. Celle-ci affiche douze heures 45. À sa droite, il est écrit « plus trois
quart » à cinq reprises. Sous chaque fraction il y a une flèche qui pointe à droite vers la dernière horloge. Celle-ci
affiche quatre heures 30.
Image L’illustration montre des horloges, des flèches et des fractions toutes alignées côte à côte. La
première horloge affiche douze heures. À sa droite, il est écrit « plus trois quarts » au-dessus d’une flèche qui
pointe à droite vers la prochaine horloge. Celle-ci affiche douze heures 45. À sa droite, il est écrit « plus trois
quart » à cinq reprises. Sous chaque fraction il y a une flèche qui pointe à droite vers la dernière horloge. Celle-ci
affiche quatre heures 30.
- utiliser une représentation semi-concrète;
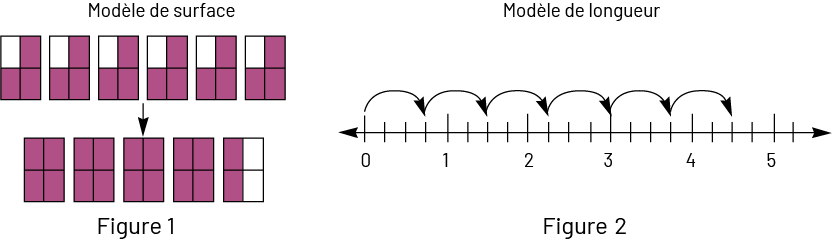 Deux illustrations sont présentées : figure un et figure deux. La figure un s’intitule Modèle de surface. Il y a six
rectangles alignés côte à côte, tous identiques. Ils sont
divisés en quatre parties égales, la première partie est blanche et les trois autres sont pourpre. Sous ceux-ci, une
flèche vers le bas pointe vers cinq rectangles divisés en quatre, alignés côte à côte. Les quatre premiers
rectangles sont entièrement pourpres, tandis que le cinquième est pourpre aux deux parties à gauche et blanc aux
deux parties à droite. La figure deux s’intitule Modèle de longueur. C’est une double droite numérique graduée de zéro
à cinq avec marques
d’intervalles à zéro virgule 25. Une flèche relie zéro à zéro virgule 75. Une flèche relie zéro virgule 75 à un
virgule cinq. Une flèche relie zéro virgule cinq à deux virgule 25. Une flèche relie deux virgule 25 à trois. Une
flèche relie trois à trois virgule 75. Et une flèche relie trois virgule 75 à quatre virgule cinq.
Deux illustrations sont présentées : figure un et figure deux. La figure un s’intitule Modèle de surface. Il y a six
rectangles alignés côte à côte, tous identiques. Ils sont
divisés en quatre parties égales, la première partie est blanche et les trois autres sont pourpre. Sous ceux-ci, une
flèche vers le bas pointe vers cinq rectangles divisés en quatre, alignés côte à côte. Les quatre premiers
rectangles sont entièrement pourpres, tandis que le cinquième est pourpre aux deux parties à gauche et blanc aux
deux parties à droite. La figure deux s’intitule Modèle de longueur. C’est une double droite numérique graduée de zéro
à cinq avec marques
d’intervalles à zéro virgule 25. Une flèche relie zéro à zéro virgule 75. Une flèche relie zéro virgule 75 à un
virgule cinq. Une flèche relie zéro virgule cinq à deux virgule 25. Une flèche relie deux virgule 25 à trois. Une
flèche relie trois à trois virgule 75. Et une flèche relie trois virgule 75 à quatre virgule cinq.
- utiliser une disposition rectangulaire;
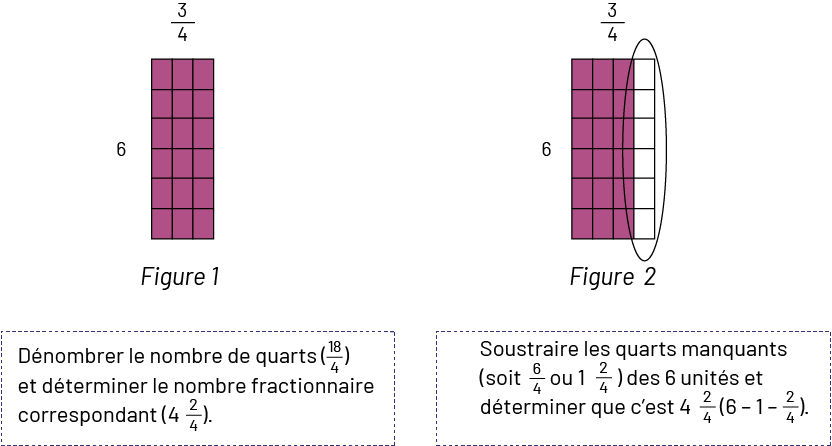 Image Deux illustrations sont présentées : figure un et figure deux. La figure un est un rectangle
vertical divisé en six rangées de trois parties égales. Toutes les parties sont
pourpres. À gauche du rectangle, il est écrit six, et en haut, il est écrit trois quarts. Sous le rectangle, il y a
un encadré textuel qui dit : Dénombrer le nombre de quarts, dix-huit quarts, et déterminer le nombre fractionnaire
correspondant, quatre et deux quarts. La figure deux est un rectangle divisé en six rangées de quatre parties égales.
Les trois premières colonnes sont
pourpres tandis que la dernière est blanche. À gauche, il est écrit six, et en haut, il est écrit trois quarts. En
dessous, il y a l’encadré textuel suivant : Soustraire les quarts manquants, soit six quarts ou un et deux quarts
des six unités et déterminer que c’est quatre et deux quarts parenthèse ouvrante six moins un moins deux quarts
parenthèse fermante.
Image Deux illustrations sont présentées : figure un et figure deux. La figure un est un rectangle
vertical divisé en six rangées de trois parties égales. Toutes les parties sont
pourpres. À gauche du rectangle, il est écrit six, et en haut, il est écrit trois quarts. Sous le rectangle, il y a
un encadré textuel qui dit : Dénombrer le nombre de quarts, dix-huit quarts, et déterminer le nombre fractionnaire
correspondant, quatre et deux quarts. La figure deux est un rectangle divisé en six rangées de quatre parties égales.
Les trois premières colonnes sont
pourpres tandis que la dernière est blanche. À gauche, il est écrit six, et en haut, il est écrit trois quarts. En
dessous, il y a l’encadré textuel suivant : Soustraire les quarts manquants, soit six quarts ou un et deux quarts
des six unités et déterminer que c’est quatre et deux quarts parenthèse ouvrante six moins un moins deux quarts
parenthèse fermante.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 95-96.
- effectuer des calculs.
À la suite de l’utilisation de divers modèles, certains élèves remarquent souvent qu’elles et ils peuvent déterminer le produit à l’aide de calculs. Par exemple, afin de calculer \(6\; \times \;\frac{3}{4}\), je multiplie d’abord 6 par 3, puis je divise ce résultat par 4 et j’obtiens \(\frac{{18}}{4}\;\;\;{\rm{ou}}\;\;\;{\rm{4}}\frac{2}{4}\).
Cette dernière stratégie quoiqu’elle soit efficace ne doit pas être appliquée sans compréhension. Il est important que les élèves réalisent que lorsqu’elles et ils effectuent la multiplication \(6\; \times \;3\), elles et ils déterminent le nombre de morceaux. Puisque ces morceaux sont des quarts, elles et ils ont alors déterminé qu’il y a un total de 18 quarts (\(\frac{{18}}{4}\)).
 Image Six carrés divisés en quatre carrés égaux sont alignés côte à côte. La description va de gauche à droite et
de haut en bas. Le premier carré présente les chiffres un, deux et trois dans ses trois premiers carrés, qui sont
aussi jaunes. Le
quatrième carré est vide et blanc. Le deuxième carré est identique, mais avec les chiffres quatre, cinq, six. Le
troisième carré est identique, mais avec les chiffres sept, huit, neuf. Le quatrième carré est identique, mais avec
les chiffres dix, onze, douze. Le cinquième carré est identique, mais avec les chiffres 13, 14, 15. Le sixième carré
est identique, mais avec les chiffres 16, 17, 18.
Image Six carrés divisés en quatre carrés égaux sont alignés côte à côte. La description va de gauche à droite et
de haut en bas. Le premier carré présente les chiffres un, deux et trois dans ses trois premiers carrés, qui sont
aussi jaunes. Le
quatrième carré est vide et blanc. Le deuxième carré est identique, mais avec les chiffres quatre, cinq, six. Le
troisième carré est identique, mais avec les chiffres sept, huit, neuf. Le quatrième carré est identique, mais avec
les chiffres dix, onze, douze. Le cinquième carré est identique, mais avec les chiffres 13, 14, 15. Le sixième carré
est identique, mais avec les chiffres 16, 17, 18.
Par la suite, lorsqu’elles et ils effectuent \(18\; \div \;4\), elles et ils déterminent le nombre de groupements de 4 quarts. Ainsi, elles et ils déterminent qu’il y a 4 touts et il reste deux quarts, d’où le résultat \(4\frac{2}{4}\).
 Image Cinq carrés divisés en quatre carrés égaux sont alignés côte à
côte. Tandis que les quatre premiers carrés sont entièrement jaunes, le cinquième carré a deux petits carrés jaunes à
gauche et deux petits carrés blancs à droite.
Image Cinq carrés divisés en quatre carrés égaux sont alignés côte à
côte. Tandis que les quatre premiers carrés sont entièrement jaunes, le cinquième carré a deux petits carrés jaunes à
gauche et deux petits carrés blancs à droite.
Multiplication d’une fraction par un nombre fractionnaire
Exemples
Note : Pour calculer l’aire d’un rectangle, il faut multiplier les deux dimensions, ce qui équivaut à la formule de l’aire.
A = longueur × largeur
\(\frac{2}{5}\; \times \;2\frac{1}{4}\;\)
- Multiplication effectuée à l’aide de la disposition rectangulaire
Je décompose le nombre \(2\frac{1}{4}\) en \(2\; + \;\frac{1}{4}\).
 Image Un
rectangle horizontal possède un trait vertical vers sa droite qui le sépare en deux parties. La largeur mesure deux
sur cinq, tandis que la longueur mesure deux pour la grande partie et un quart pour la petite partie.
Image Un
rectangle horizontal possède un trait vertical vers sa droite qui le sépare en deux parties. La largeur mesure deux
sur cinq, tandis que la longueur mesure deux pour la grande partie et un quart pour la petite partie.
J’effectue les multiplications partielles.
Je sais que \(2\; \times \;\frac{2}{5}\) est la même chose que \(\frac{2}{5}\; + \;\frac{2}{5}\), ce qui me donne \(\frac{4}{5}\).
Pour effectuer \(\frac{2}{5}\; \times \;\frac{1}{4}\), je multiplie les numérateurs ensemble et je multiplie les dénominateurs ensemble. Alors, \(\frac{2}{5}\; \times \;\frac{1}{4}\; = \;\frac{2}{{20}}\;{\rm{ou}}\;\frac{1}{{10}}\).
 Image Un rectangle horizontal possède un trait vertical vers sa droite
qui le sépare en deux parties. La largeur mesure deux sur cinq, tandis que la longueur mesure deux pour la grande
partie et un quart pour la petite partie. Il est écrit quatre sur cinq dans la grande partie et un sur dix dans la
petite partie.
Image Un rectangle horizontal possède un trait vertical vers sa droite
qui le sépare en deux parties. La largeur mesure deux sur cinq, tandis que la longueur mesure deux pour la grande
partie et un quart pour la petite partie. Il est écrit quatre sur cinq dans la grande partie et un sur dix dans la
petite partie.
Je dois maintenant additionner les produits partiels. Je trouve un dénominateur commun, soit des dixièmes.
\(\begin{align} \frac{4}{5}\; + \;\frac{1}{{10}}\; &= \;\frac{8}{{10}}\; + \frac{1}{{10}} \\ &= \;\frac{9}{{10}} \end{align}\)
Alors, \(\frac{2}{5}\; \times \;2\frac{1}{4}\; = \;\frac{9}{{10}}\).
- Multiplication effectuée en transformant le nombre fractionnaire en fraction impropre
Je transforme tout d’abord \(2\frac{1}{4}\)en fraction impropre, soit \(\frac{9}{4}\)puisque \(\frac{4}{4}\; + \;\frac{4}{4}\; + \;\frac{1}{4}\; = \;\frac{9}{4}\) (distributivité).
Maintenant, je peux multiplier les deux fractions en multipliant les numérateurs ensemble et en multipliant les dénominateurs ensemble.
\(\begin{align}\frac{2}{5}\; \times \;2\frac{1}{4}\; &= \;\frac{2}{5}\; \times \;\frac{9}{4}\\ &= \;\frac{{18}}{{20}}\;\;\;{\rm{ou}}\;\;\;\frac{9}{{10}}\end{align}\)
Alors, \(\frac{2}{5}\; \times \;2\frac{1}{4}\; = \;\frac{9}{{10}}\).
\(1\frac{1}{3}\; \times \;2\frac{3}{4}\)
- Multiplication effectuée à l’aide de la disposition rectangulaire
Je décompose le nombre fractionnaire \(1\frac{1}{3}\;\;\;{\rm{en}}\;\;\;{\rm{1}}\;{\rm{ + }}\;\frac{1}{3}\) et \(2\frac{3}{4}\;\;\;{\rm{et}}\;\;\;{\rm{2}}\;{\rm{ + }}\;\frac{3}{4}\).
J’effectue les multiplications partielles.
\(\begin{align} \left( {1\; + \;\frac{1}{3}} \right) \left( {2\; + \;\frac{3}{4}} \right)\; &= \;\left( {1\; \times \;2} \right)\; + \;\left( {1\; \times \;\frac{3}{4}} \right)\; + \;\left( {2\; \times \;\frac{1}{3}} \right)\; + \;\left( {\frac{1}{3}\; \times \;\frac{3}{4}} \right)\\ &= \;2\; + \;\frac{3}{4}\; + \;\frac{2}{3}\; + \;\frac{3}{{12}}\end{align}\)
J’additionne tous les produits partiels.
\(\begin{align}2\; + \;\frac{3}{4}\; + \;\frac{2}{3}\; + \;\frac{3}{{12}}\; &= \;2\; + \;\frac{9}{{12}}\; + \;\frac{8}{{12}}\; + \;\frac{3}{{12}}\\ &= \;2\; + \;\frac{{20}}{{12}}\\ &= \;2\; + \;1\frac{8}{{12}}\\ &= \;3\frac{8}{{12}}\;\;\;{\rm{ou}}\;\;\;{\rm{3}}\frac{2}{3} \\ {\rm{Alors,}}\; \;1\frac{1}{3} \times \; \;2\frac{3}{4} \; &= \;3\frac{2}{3}\end{align}\)
- Multiplication effectuée en transformant les nombres fractionnaires en fractions impropres
Je transforme les deux nombres fractionnaires en fractions impropres.
\(\begin{align}1\frac{1}{3}\; &= \;\frac{3}{3}\; + \;\frac{1}{3} \\ &= \;\frac{4}{3}\end{align}\) \(\begin{align}2\frac{3}{4}\; &= \;\frac{4}{4}\; + \;\frac{4}{4}\; + \;\frac{3}{4} \\ &= \frac{{11}}{4}\end{align}\)
Maintenant, je peux multiplier les deux fractions impropres en multipliant les numérateurs ensemble et en multipliant les dénominateurs ensemble.
\(\begin{align}\frac{4}{3}\; \times \;\frac{{11}}{4} &= \;\frac{{44}}{{12}} \\ &= 3\frac{8}{{12}}\;\; ou \;\; {\rm{3}}\frac{2}{3}\end{align}\)
Division
Lorsqu’on divise des fractions, il y a une certaine progression à suivre. L’exploration de la division, comme celle des autres opérations, doit miser sur les représentations concrètes et semi-concrètes et non sur les algorithmes. Les élèves peuvent alors réactiver leurs connaissances antérieures et saisir le sens de l’opération. Afin de comprendre une division, il est essentiel d’examiner le sens de la division et la nature des nombres qui la composent. Une division a le sens de partage lorsqu’on cherche la taille des groupes; elle a le sens de groupement lorsqu’on cherche le nombre de groupes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 79-80.
Division d’une fraction par un nombre naturel
On retrouve plus souvent la division d’une fraction par un nombre naturel (par exemple, \(\frac{3}{4}\; \div \;5\)) dans des situations de partage. On peut commencer par des situations dans lesquelles le numérateur est divisible par le diviseur (par exemple, \(\frac{6}{9}\; \div \;3,\;\frac{3}{4}\; \div \;3,\;\frac{4}{9}\; \div \;2,\;\frac{{12}}{{20}}\; \div \;4\)). Les exemples ci-dessous montrent différentes façons d’obtenir le résultat de la division de \(\frac{6}{9}\;{\rm{par}}\;{\rm{3}}\).
Exemples de représentations de \(\frac{6}{9}\; \div \;3\; = \;\frac{2}{9}\)
| Modèle de surface | Modèle de longueur | Modèle d’ensemble |
|---|---|---|
| Trois amies veulent se partager \(\frac{6}{9}\) d’une tarte. Combien chacune recevra-t-elle? | Trois sœurs s’en vont à l’école et il reste \(\frac{6}{9}\) de la distance à parcourir. À tour de
rôle, chacune aura le cellulaire qu’elles partagent. Sur quelle fraction de la distance totale
chaque sœur écoutera-t-elle de la musique?
|
Dans un sac, il y avait des bonbons. Pierre en a mangé et il reste \(\frac{6}{9}\) des bonbons. Trois amies veulent se les partager. Quelle fraction des bonbons chaque amie recevra-t-elle? |
 Image Un cercle est divisé en neuf parties égales. Il y a six parties bleues et trois
parties violettes. Un trait gras sépare les parties bleues par groupes de deux, au-dessus desquels il est
écrit deux sur neuf. Les parties violettes sont divisées par des pointillés. Image Un cercle est divisé en neuf parties égales. Il y a six parties bleues et trois
parties violettes. Un trait gras sépare les parties bleues par groupes de deux, au-dessus desquels il est
écrit deux sur neuf. Les parties violettes sont divisées par des pointillés. |
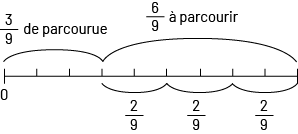 Image Une ligne de dénombrement partant de zéro est divisée en neuf marques d’intervalles.
Au-dessus de la ligne, un tracé courbé lie zéro à la troisième marque en indiquant trois neuvièmes de
parcourue. Un tracé courbé lie trois neuvièmes à la fin de la ligne en indiquant six neuvièmes à parcourir.
Sous la ligne, un tracé courbé relie la troisième marque à la cinquième en indiquant deux neuvièmes. Un
tracé courbé relie la cinquième marque à la septième en indiquant deux neuvièmes. Et un tracé courbé relie
la septième marque à la neuvième en indiquant deux neuvièmes. Image Une ligne de dénombrement partant de zéro est divisée en neuf marques d’intervalles.
Au-dessus de la ligne, un tracé courbé lie zéro à la troisième marque en indiquant trois neuvièmes de
parcourue. Un tracé courbé lie trois neuvièmes à la fin de la ligne en indiquant six neuvièmes à parcourir.
Sous la ligne, un tracé courbé relie la troisième marque à la cinquième en indiquant deux neuvièmes. Un
tracé courbé relie la cinquième marque à la septième en indiquant deux neuvièmes. Et un tracé courbé relie
la septième marque à la neuvième en indiquant deux neuvièmes. |
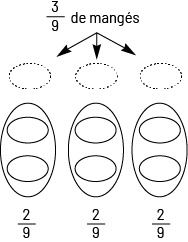 Image De haut en bas, l’illustration commence avec le court texte « trois neuvièmes de
mangés ». Celui-ci pointe avec trois flèches vers trois ovales horizontaux pointillés placés côte à côte.
Sous chacun d’eux, il y a un grand ovale vertical contenant deux ovales horizontaux. Et sous ceux-ci, il est
écrit deux neuvièmes. Image De haut en bas, l’illustration commence avec le court texte « trois neuvièmes de
mangés ». Celui-ci pointe avec trois flèches vers trois ovales horizontaux pointillés placés côte à côte.
Sous chacun d’eux, il y a un grand ovale vertical contenant deux ovales horizontaux. Et sous ceux-ci, il est
écrit deux neuvièmes. |
Les élèves peuvent ensuite s’attaquer à des situations de divisions plus complexes, où le numérateur n’est pas divisible par le diviseur (par exemple, \(\frac{2}{3}\; \div \;6,\;\frac{3}{5}\; \div \;12\)).
La complexité vient du fait que la situation est plus difficile à représenter. Pour réussir, il faut bien comprendre que le partage dans ces situations implique de subdiviser les parties. L’opération est plus facile à comprendre lorsqu’elle est présentée en situation.
Exemple 1
Dans la vidéo suivante, un groupe d’élèves divise un nombre fractionnaire par un nombre naturel à l’aide du matériel de base 10.
 Description de la vidéo
Description de la vidéo
Description à venir
Exemple 2
Les 6 membres d’une famille veulent se partager les \(\frac{2}{3}\) d’une tarte. Quelle fraction de tarte chacun aura-t-il?
La question éclaircit ce que l’on cherche, c’est-à-dire une fraction d’une tarte complète. En reconnaissant que la division est associée au concept de partage, on peut représenter la situation de façon symbolique par \(\frac{2}{3}\; \div \;6\). Afin de représenter l’opération, on peut illustrer \(\frac{2}{3}\) d’une tarte.
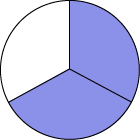
Comment partage-t-on ces deux tiers? On peut diviser chaque tiers en trois morceaux égaux pour un total de six morceaux égaux (Figure 1). On peut aussi diviser le premier tiers en six morceaux qui seront partagés, puis faire de même avec le deuxième tiers (Figure 2).
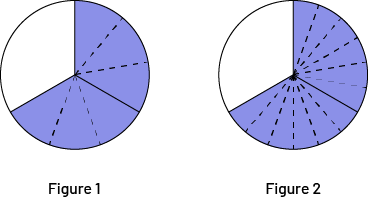 Image La figure un est un cercle divisé en sept parties égales,
violettes, et une plus grande partie, blanche. Les
sept parties sont séparées par un pointillé sauf de la troisième à la quatrième, où le trait est plein.
La figure deux est un cercle divisé en douze parties égales, violettes, et une grande partie blanche. Les parties
violettes sont séparées par un pointillé sauf de la sixième à la septième, où le trait est plein.
Image La figure un est un cercle divisé en sept parties égales,
violettes, et une plus grande partie, blanche. Les
sept parties sont séparées par un pointillé sauf de la troisième à la quatrième, où le trait est plein.
La figure deux est un cercle divisé en douze parties égales, violettes, et une grande partie blanche. Les parties
violettes sont séparées par un pointillé sauf de la sixième à la septième, où le trait est plein.
Dans les problèmes de division, la principale difficulté éprouvée par les élèves est de trouver la quantité en relation avec le tout. Dans la situation précédente (\(\frac{2}{3}\; \div \;6\)), la fraction \(\frac{2}{3}\) agit temporairement comme un tout, car elle doit être divisée en 6. Cependant, on doit exprimer la réponse par rapport au tout auquel \(\frac{2}{3}\) se rapporte (la tarte). Ainsi, d’après les représentations ci-dessus, l’élève détermine que la solution est 1 morceau ou 2 morceaux selon le partage effectué, mais a du mal à reconnaître qu’il s’agit de 1 ou de 2 morceaux du tout. Mais comment sait-on quelle fraction de tarte chacun reçoit? Pour le savoir, il faut aussi diviser le tiers manquant.
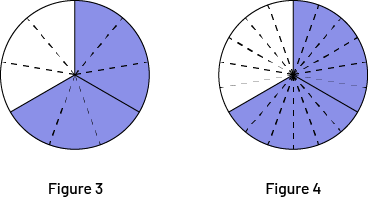 Image La figure trois est un cercle divisé en neuf parties égales, toutes séparées par un pointillé sauf entre la
troisième et la quatrième, où le trait est plein. Six parties sont violettes et trois parties sont blanches. La
figure quatre est un cercle divisé en 18 parties égales. Elles sont séparées par un pointillé sauf entre la
sixième et la septième partie, où le trait est plein. Entre la cinquième et la sixième, et entre la treizième et la
quatorzième, le pointillé est plus pâle. Douze parties sont violettes et six parties sont blanches.
Image La figure trois est un cercle divisé en neuf parties égales, toutes séparées par un pointillé sauf entre la
troisième et la quatrième, où le trait est plein. Six parties sont violettes et trois parties sont blanches. La
figure quatre est un cercle divisé en 18 parties égales. Elles sont séparées par un pointillé sauf entre la
sixième et la septième partie, où le trait est plein. Entre la cinquième et la sixième, et entre la treizième et la
quatorzième, le pointillé est plus pâle. Douze parties sont violettes et six parties sont blanches.
Ainsi, selon le premier fractionnement, chacun reçoit un morceau, soit \(\frac{1}{9}\) de tarte (Figure 3). Selon le deuxième, chacun reçoit deux morceaux, soit \(\frac{2}{{18}}\) de tarte (Figure 4). Cependant, il s’agit de la même quantité puisque \(\frac{1}{9}\) et \(\frac{2}{{18}}\) sont des fractions équivalentes.
Considérons la même division (\(\frac{2}{3}\; \div \;6\)) issue d’une situation qui se rapporte plutôt au modèle de longueur.
Exemple 3
On veut couper \(\frac{2}{3}\) d’un rouleau de corde en 6 sections. Quelle fraction du rouleau de corde chaque section représentera-t-elle?
Lorsque l’on saisit le sens du problème, on peut reconnaître qu’on doit effectuer \(\frac{2}{3}\; \div \;6\). Afin de déterminer le quotient, comme dans l’exemple précédent, on peut procéder de deux façons :
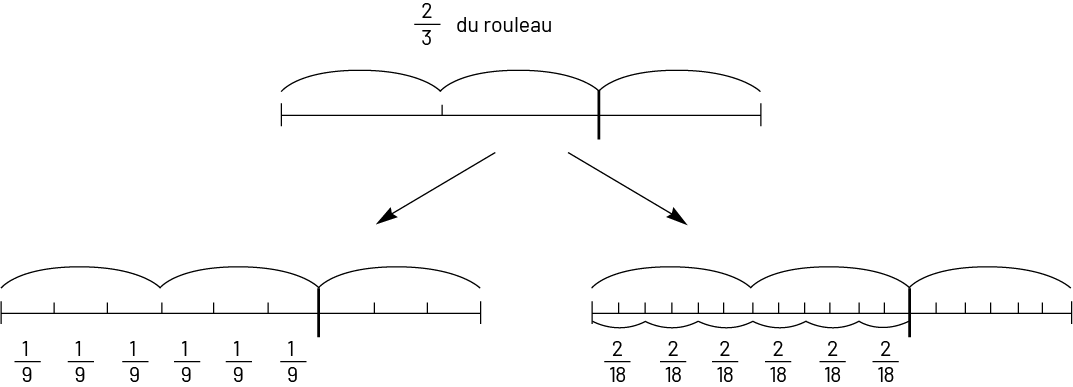 Image Tout en haut de l’illustration, il est écrit « deux tiers du rouleau ». En dessous, il y a une ligne
horizontale marquée d’un trait d’intervalle aux deux tiers. Au-dessus de la ligne, des tracés courbes relient le
début de la ligne au tiers, le tiers de la ligne aux deux tiers et les deux tiers de la ligne à la fin. Sous la
ligne, une flèche pointe en bas à gauche et une flèche pointe en bas à droite. En bas à gauche, il y a une ligne de
dénombrement séparée en neuf. Sous les six premiers neuvièmes, il est écrit un
neuvième. Un plus long trait les divise des trois neuvièmes restants. Au-dessus de la ligne, des tracés courbes
relient le début de la ligne au tiers, le tiers de la ligne aux deux tiers et les deux tiers de la ligne à la fin.
En bas à droite, il y a une ligne de dénombrement séparée en 18. Sous les douze premier dix-huitièmes, un trait
courbe les unit par deux en indiquant deux dix-huitièmes. Un plus long trait les divise des six dix-huitièmes
restants. Au-dessus de la ligne, des tracés courbes relient le début de la ligne au tiers, le tiers de la ligne aux
deux tiers et les deux tiers de la ligne à la fin.
Image Tout en haut de l’illustration, il est écrit « deux tiers du rouleau ». En dessous, il y a une ligne
horizontale marquée d’un trait d’intervalle aux deux tiers. Au-dessus de la ligne, des tracés courbes relient le
début de la ligne au tiers, le tiers de la ligne aux deux tiers et les deux tiers de la ligne à la fin. Sous la
ligne, une flèche pointe en bas à gauche et une flèche pointe en bas à droite. En bas à gauche, il y a une ligne de
dénombrement séparée en neuf. Sous les six premiers neuvièmes, il est écrit un
neuvième. Un plus long trait les divise des trois neuvièmes restants. Au-dessus de la ligne, des tracés courbes
relient le début de la ligne au tiers, le tiers de la ligne aux deux tiers et les deux tiers de la ligne à la fin.
En bas à droite, il y a une ligne de dénombrement séparée en 18. Sous les douze premier dix-huitièmes, un trait
courbe les unit par deux en indiquant deux dix-huitièmes. Un plus long trait les divise des six dix-huitièmes
restants. Au-dessus de la ligne, des tracés courbes relient le début de la ligne au tiers, le tiers de la ligne aux
deux tiers et les deux tiers de la ligne à la fin.
Ainsi, on peut déterminer que chacune des 6 sections correspond à \(\frac{1}{9}\) ou \(\frac{2}{{18}}\) du rouleau de corde.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97-100.
Division d’un nombre naturel par une fraction
Ainsi, en 5e année, la division d’un nombre naturel par une fraction unitaire (par exemple, \(2\; \div \;\frac{1}{3}\)) se représente bien en utilisant le sens de groupement. Dans ce cas, la fraction est le diviseur.

Par exemple, si on a 2 réglisses et que l’on veut remettre à chaque enfant \(\frac{1}{3}\) d’une réglisse, on procède à une division puisqu’il faut séparer une quantité (2 réglisses) en des quantités égales (\(\frac{1}{3}\) de réglisse) pour déterminer le nombre de quantités égales ou de groupes qui peuvent être créés (6 enfants recevront \(\frac{1}{3}\) de réglisse chacun). Dans ce cas, il est important de reconnaître que le quotient exprime un nombre de sections, soit des tiers et non une quantité d’objets (réglisses).
 Image
Trois ensembles de réglisses.
Le premier ensemble, qui comporte deux réglisses, pointe avec une flèche vers le deuxième ensemble, qui comporte six
réglisses placées deux par deux. Le premier paquet de deux pointe avec une flèche vers la troisième réglisse du
troisième ensemble, qui comporte six réglisses alignées et numérotées.
Image
Trois ensembles de réglisses.
Le premier ensemble, qui comporte deux réglisses, pointe avec une flèche vers le deuxième ensemble, qui comporte six
réglisses placées deux par deux. Le premier paquet de deux pointe avec une flèche vers la troisième réglisse du
troisième ensemble, qui comporte six réglisses alignées et numérotées.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 80-82.
Dans le cas d’une division d’un nombre naturel par une fraction, la division prend généralement le sens de groupement. Ainsi, l’analogie de la soustraction répétée est de mise puisqu’il s’agit de séparer des parties.
Par exemple, dans la division de 2 par \(\frac{1}{4}\) (\(2\; \div \;\frac{1}{4}\)), en faisant \(2\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\), on peut créer 8 groupes de \(\frac{1}{4}\). Cependant, le groupe créé est plutôt abstrait puisqu’il s’agit d’un groupe qui est une fraction d’un tout. Les questions « Combien de \(\frac{1}{4}\) peuvent être créés avec 2 touts? » et « Combien de fois \(\frac{1}{4}\) va-t-il dans 2? » peuvent aider à se représenter l’opération.
En 6e année, l’élève divise un nombre naturel par une fraction propre.
Exemple
\(6\; \div \;\frac{3}{5}\; = \;10\)
Modèle de surface
Afin de créer un dallage, chaque équipe a besoin de l’équivalent des \(\frac{3}{5}\;\)des carrés d’une feuille. Combien d’équipes peuvent effectuer la tâche si on dispose de 6 feuilles?
 Image Six carrés sont disposés en deux rangées de trois. Ils sont tous divisés en cinq parts égales qui forment des
rectangles verticaux. Premier carré : Les trois premiers rectangles sont pourpres et les deux autres sont jaunes. Le
chiffre un est placé
sur le deuxième rectangle. Le chiffre deux est placé entre le premier et le deuxième carré. Deuxième carré : Le
premier et le dernier rectangle sont jaunes et les trois rectangles du centre sont pourpres. Le
chiffre trois est placé sur le troisième rectangle. Le chiffre quatre est placé entre le deuxième et le troisième
carré. Troisième carré : les deux premiers rectangles sont jaunes tandis que les trois autres sont pourpres. Le
chiffre
cinq est placé sur le quatrième rectangle. Quatrième carré : les trois premiers rectangles sont jaunes et les deux
derniers sont pourpres. Le chiffre six est
placé sur le deuxième rectangle. Le chiffre sept est placé entre le quatrième et le cinquième carré. Cinquième carré
: le premier et le dernier rectangle sont pourpres et les trois rectangles du centre sont jaunes.
Le chiffre huit est placé sur le troisième rectangle. Le chiffre neuf est placé entre le cinquième et le sixième
carré. Sixième carré : Les deux premiers rectangles sont pourpres et les trois derniers sont jaunes. Le nombre dix
est
placé sur le quatrième rectangle.
Image Six carrés sont disposés en deux rangées de trois. Ils sont tous divisés en cinq parts égales qui forment des
rectangles verticaux. Premier carré : Les trois premiers rectangles sont pourpres et les deux autres sont jaunes. Le
chiffre un est placé
sur le deuxième rectangle. Le chiffre deux est placé entre le premier et le deuxième carré. Deuxième carré : Le
premier et le dernier rectangle sont jaunes et les trois rectangles du centre sont pourpres. Le
chiffre trois est placé sur le troisième rectangle. Le chiffre quatre est placé entre le deuxième et le troisième
carré. Troisième carré : les deux premiers rectangles sont jaunes tandis que les trois autres sont pourpres. Le
chiffre
cinq est placé sur le quatrième rectangle. Quatrième carré : les trois premiers rectangles sont jaunes et les deux
derniers sont pourpres. Le chiffre six est
placé sur le deuxième rectangle. Le chiffre sept est placé entre le quatrième et le cinquième carré. Cinquième carré
: le premier et le dernier rectangle sont pourpres et les trois rectangles du centre sont jaunes.
Le chiffre huit est placé sur le troisième rectangle. Le chiffre neuf est placé entre le cinquième et le sixième
carré. Sixième carré : Les deux premiers rectangles sont pourpres et les trois derniers sont jaunes. Le nombre dix
est
placé sur le quatrième rectangle.
Modèle de longueur
Une enseignante a une corde de 6 m et veut la couper en sections de \(\frac{3}{5}\;\)de mètre chacune. Combien de sections pourra-t-elle créer?
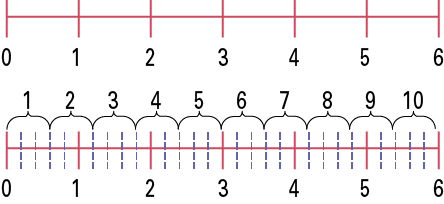 Image Deux droites numériques graduées de zéro à six sont placées l’une sous l’autre. La première ne présente que
les chiffres de zéro à six. La deuxième les présente aussi mais possède également des marques d’intervalles de zéro
virgule deux en pointillé.
Au-dessus, l'accolade un regroupe zéro à zéro virgule six. L’accolade deux regroupe zéro virgule six à un virgule
deux. L’accolade trois regroupe un virgule deux à un virgule huit. L’accolade quatre regroupe un virgule huit à deux
virgule quatre. L’accolade cinq regroupe deux virgule quatre à trois. L’accolade six regroupe trois à trois virgule
six. L’accolade sept regroupe trois virgule six à quatre virgule deux. L’accolade huit regroupe quatre virgule deux
à quatre virgule huit. L’accolade neuf regroupe quatre virgule huit à cinq virgule quatre. Et l’accolade dix
regroupe cinq virgule quatre à six.
Image Deux droites numériques graduées de zéro à six sont placées l’une sous l’autre. La première ne présente que
les chiffres de zéro à six. La deuxième les présente aussi mais possède également des marques d’intervalles de zéro
virgule deux en pointillé.
Au-dessus, l'accolade un regroupe zéro à zéro virgule six. L’accolade deux regroupe zéro virgule six à un virgule
deux. L’accolade trois regroupe un virgule deux à un virgule huit. L’accolade quatre regroupe un virgule huit à deux
virgule quatre. L’accolade cinq regroupe deux virgule quatre à trois. L’accolade six regroupe trois à trois virgule
six. L’accolade sept regroupe trois virgule six à quatre virgule deux. L’accolade huit regroupe quatre virgule deux
à quatre virgule huit. L’accolade neuf regroupe quatre virgule huit à cinq virgule quatre. Et l’accolade dix
regroupe cinq virgule quatre à six.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 102.
Rendu en 7e année, l’élève divise des fractions par d’autres fractions.
Division d’une fraction par une fraction
La vidéo suivante montre la division d’une fraction par une autre fraction à l’aide d’un modèle de surface et d’un algorithme.
 Description de la vidéo
Description de la vidéo
Description à venir
Voici d’autres exemples de division de fractions, soient la division sans fractionnement et la division avec fractionnement.
Division sans fractionnement
Exemple
\(\frac{5}{6}\; \div \;\frac{1}{6}\)
- Division effectuée à l’aide du modèle de modèle de surface
Je représente \(\frac{5}{6}\) d’un rectangle en divisant le rectangle en 6 parties égales dont 5 parties sont ombragées. Je me pose la question « Combien de \(\frac{1}{6}\) y a-t-il dans \(\frac{5}{6}\)? »
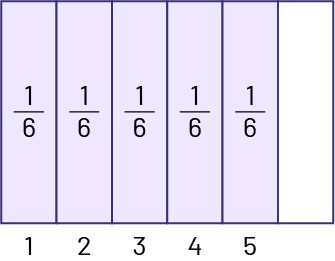 Image Un rectangle est divisé en six parties égales sur le sens de la largeur. Les cinq premières
parties sont bleues et portent la fraction un sixième. Il est écrit respectivement un, deux, trois, quatre et cinq
sous ces parties. La sixième partie est blanche et ne possède aucune mention.
Image Un rectangle est divisé en six parties égales sur le sens de la largeur. Les cinq premières
parties sont bleues et portent la fraction un sixième. Il est écrit respectivement un, deux, trois, quatre et cinq
sous ces parties. La sixième partie est blanche et ne possède aucune mention.
Il y a 5 un sixième dans \(\frac{5}{6}\). Alors, \(\frac{5}{6}\; \div \;\frac{1}{6}\; = \;5\).
- Division effectuée à l’aide d’une représentation symbolique
Étant donné que le dividende et le diviseur ont un dénominateur commun, je peux diviser les numérateurs et diviser les dénominateurs.
\(\begin{align}\frac{5}{6}\; \div \;\frac{1}{6}\; &= \;\frac{{5\; \div \;1}}{{6\; \div \;6}}\\ &= \;\frac{5}{1}\\ &= \;5 \end{align}\)
Division avec fractionnement
Exemple
\(\frac{3}{4}\; \div \;\frac{1}{2}\)
- Division effectuée à l’aide d’une droite numérique
Je représente \(\frac{3}{4}\)sur la droite numérique (trait rouge). Je me pose la question « Combien y a-t-il de groupes de \(\frac{1}{2}\) dans \(\frac{3}{4}\)? »
En sachant que \(\frac{2}{4}\; = \;\frac{1}{2}\), je détermine combien de \(\frac{2}{4}\) il y a dans \(\frac{3}{4}\).
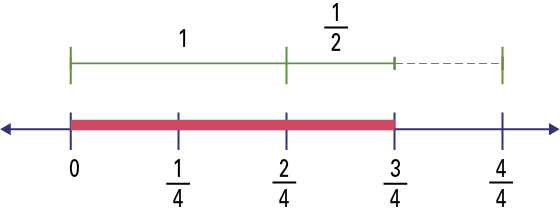 Image Une double droite numérique est graduée de zéro à quatre quarts
avec marques d’intervalles aux quarts. Un trait rouge la surligne de zéro à trois quarts. Au-dessus, il y a une ligne
de zéro à quatre quarts avec une marque au centre. Il est écrit « un » au-dessus de la première moitié. La deuxième
moitié et à moitié pleine et à moitié pointillée. Il est écrit « un demi » au-dessus de la partie pleine.
Image Une double droite numérique est graduée de zéro à quatre quarts
avec marques d’intervalles aux quarts. Un trait rouge la surligne de zéro à trois quarts. Au-dessus, il y a une ligne
de zéro à quatre quarts avec une marque au centre. Il est écrit « un » au-dessus de la première moitié. La deuxième
moitié et à moitié pleine et à moitié pointillée. Il est écrit « un demi » au-dessus de la partie pleine.
Sur la droite numérique ici-haut, je peux voir qu’il y a un groupe de \(\frac{1}{2}\) ou \(\frac{2}{4}\) et de \(\frac{2}{4}\) à \(\frac{3}{4}\), il y en a la moitié (\(\frac{1}{2}\)) d’un autre, donc au total il y en a 1\(\frac{1}{2}\) groupes de \(\frac{1}{2}\).
- Division effectuée à l’aide d’un dénominateur commun
\(\begin{align}\frac{3}{4}\; \div \;\frac{1}{2}\; &= \;\frac{3}{4}\; \div \;\frac{2}{4}\\ &= \;\frac{{3\; \div \;2}}{{4\; \div \;4}}\\ &= \;\frac{{\frac{3}{2}}}{1}\\ &= \;\frac{3}{2}\\ &= \;1\frac{1}{2}\end{align}\)
Division d’une fraction par un nombre fractionnaire
Exemple
\(\frac{7}{{12}}\; \div \;1\frac{3}{4}\)
- Division effectuée à l’aide d’une représentation symbolique
Je transforme le nombre fractionnaire en fraction impropre.
\(\begin{align} 1\frac{3}{4}\; &= \;\frac{4}{4}\; + \;\frac{3}{4}\; \\ &= \;\frac{7}{4} \end{align}\)
Réponse possible 1 : Je divise les numérateurs et dénominateurs.
\(\begin{align} \frac{7}{{12}}\; \div \;\frac{7}{4} &= \;\frac{{7\; \div \;7}}{{12\; \div \;4}}\\ &= \;\frac{1}{3} \end{align}\)
Alors, \(\frac{7}{{12}}\; \div \;1\frac{3}{4}\; = \;\frac{1}{3}\)
Réponse possible 2 : Je peux trouver un dénominateur commun et ensuite effectuer la division.
\(\begin{align} \frac{7}{{12}}\; \div \;\frac{7}{4}\; &= \;\frac{7}{{12}}\; \div \;\frac{{21}}{{12}}\\ &= \;\frac{{\frac{7}{21}}}{1}\\ &= \;\frac{7}{{21}}\;\;\;{\rm{ou}}\;\;\;\frac{1}{3} \end{align}\)
Alors, \(\frac{7}{{12}}\; \div \;1\frac{3}{4}\; = \;\frac{1}{3}\)
Connaissance : fraction
Le mot fraction vient du latin fractio qui veut dire « rupture ». Une partie d’un objet brisé peut donc représenter une fraction, car c’est une partie d’un tout. Toutefois, pour déterminer une fraction d’un objet divisé en plusieurs parties, il faut que les parties soient équivalentes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 33.
Connaissance : numérateur
Nombre de parties équivalentes du tout dont se compose la fraction.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Connaissance : dénominateur
Nombre de parties équivalentes par lequel le tout est divisé.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Connaissance : notation fractionnaire
La notation fractionnaire \(\frac{a}{b}\) est généralement associée au concept de partie d’un tout. Le tout peut être un élément ou un ensemble d’éléments.
Exemple :
- J’ai donné un quart (\(\frac{1}{4}\)) de mon sandwich à Alex.

- Un quart (\(\frac{1}{4}\)) de mes billes sont bleues.
 Image Un grand ovale contient deux rangées de deux petits ovales qui eux contiennent chacun deux
jetons. De gauche à droite et de haut en bas : le premier ovale contient deux jetons bleus, le deuxième ovale contient
un jeton pourpre et un jeton violet, le troisième ovale contient un jeton brun et un jeton jaune, et le quatrième
ovale contient un jeton rouge et un jeton vert.
Image Un grand ovale contient deux rangées de deux petits ovales qui eux contiennent chacun deux
jetons. De gauche à droite et de haut en bas : le premier ovale contient deux jetons bleus, le deuxième ovale contient
un jeton pourpre et un jeton violet, le troisième ovale contient un jeton brun et un jeton jaune, et le quatrième
ovale contient un jeton rouge et un jeton vert.
Or, la notation fractionnaire peut être aussi associée à d’autres concepts tels que la division, le rapport et l’opérateur.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.
