At a Glance...

B2.6 Multiply and divide fractions by fractions, as well as by whole numbers and mixed numbers, in various contexts.

Skill: Multiplying and Dividing Fractions by Fractions, by Whole Numbers and Mixed Numbers in Various Contexts

---

Multiplication

When learning to multiply fractions, students have moved through a progression since the primary grades, they have explored concepts related to multiplication using concrete materials, calculators, visuals and symbols.

By the time students are in Grade 8, they should flexibly be able to multiply and divide fractions by fractions, as well as by whole numbers and mixed numbers, in various contexts.

For example, they should be able to use an area model to solve the following problem:

In a rectangular field with an area of 100 m², Mr. Siby has planted cucumbers on \(\frac{2}{5}\)of the field. What area of the field, in m², is devoted to cucumbers?

Source: adapted from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 6e année, Module 2, Série 2, Activité 9, Activités à la carte, p. 309.

• Multiplication using an area model

I decomposed 100 into \(25\; + \;25\; + \;25\; + \;25\). I also decomposed \(\frac{2}{5}\) into \(\frac{1}{5}\; + \;\frac{1}{5}\). I know that \(\frac{1}{5}\) of 25 is 5 since \(5\; \times \;5\; = \;25\).

I added up the partial products to arrive at 40.

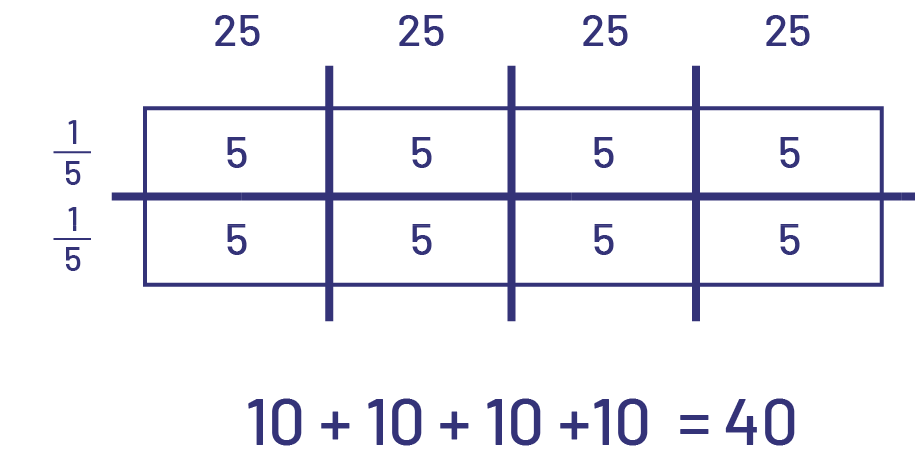
The area of the field dedicated to the cultivation of cucumbers is 40 m².

• Multiplication using a personal algorithm

The area of the field dedicated to the cultivation of cucumbers is 40 m².

Multiplying a Fraction by a Fraction

The problem-solver uses manipulatives and pictures to represent fractions and to simulate the action that results from the statement. It is from these visual representations that they construct the meaning of the operations (×, ÷).

Source: inspired by Les mathématiques… un peu, beaucoup, à la folie, Guide pédagogique, Numération et Sens du nombre/Mesure,^8e année, Module 1, Série 2, p. 143-144.

Multiplication Without Splitting

• Multiplication performed with an area model

The student can use the area model, either the rectangle or the square to multiply a fraction by another fraction.

Example

\(\frac{1}{4}\; \times \;\frac{2}{3}\) or \(\frac{1}{4}\) of \(\frac{2}{3} \)

Since I am looking for \(\frac{1}{4}\) of \(\frac{2}{3}\), I vertically divided a rectangle into 3 equal parts and coloured 2 parts, which corresponds to \( \frac{2}{3}\) of the rectangle.

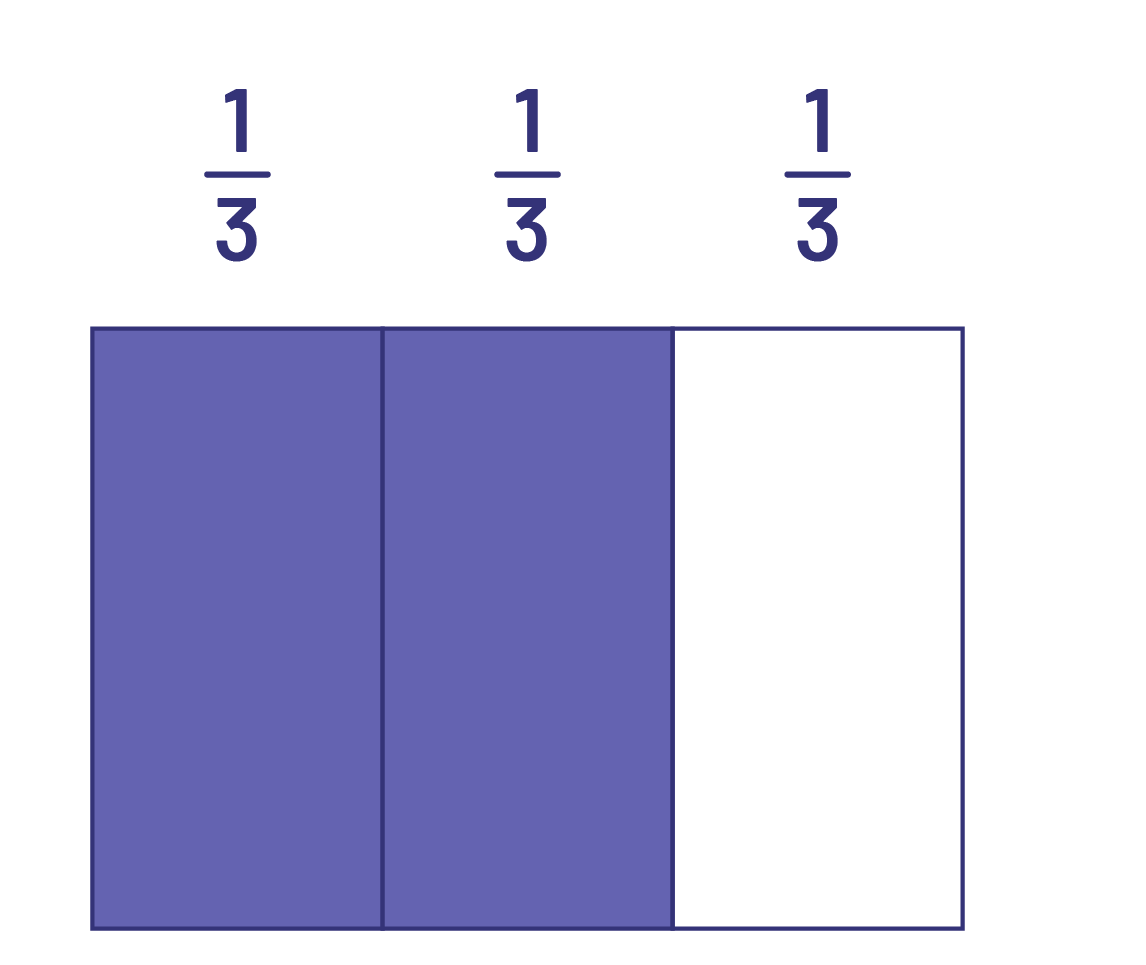
Then I horizontally divided the same rectangle into 4 equal parts and coloured 1 part, which is \(\frac{1}{4}\) of the rectangle.

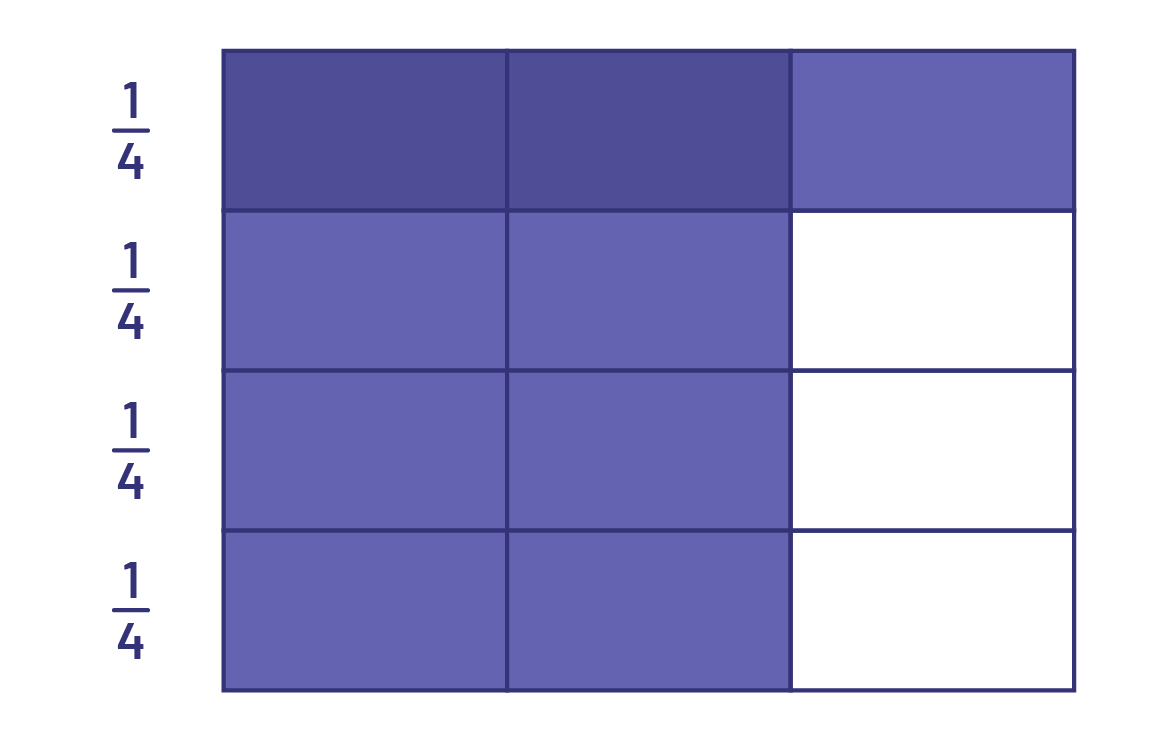
The fraction that represents \(\frac{1}{4}\) corresponds to the number of parts coloured twice, which is \(\frac{2}{{12}}\). The numerator corresponds to the darker coloured parts and the denominator corresponds to the number of parts of the same size in the whole, that is 12 parts.

The fraction \(\frac{2}{{12}}\) can be simplified to an equivalent fraction of \(\frac{1}{6}\) by halving it.

• Multiplication performed with a symbolic representation

The student multiplies the numerators together and the denominators together.

\(\frac{1}{4}\; \times \;\frac{2}{3}\; = \;\frac{{1\; \times \;2}}{{4\; \times \;3}}\)

Source: inspired by Les mathématiques… un peu, beaucoup, à la folie, Guide pédagogique, Numération et Sens du nombre/Mesure, ^8e année, Module 1, Série 2, p. 253-254.

• Multiplication performed by finding the LCM

The lowest common multiple (LCM) of 4 and 3 is 12.

I divided a rectangle into 12 equal parts (3 units by 4 units) and shaded \(\frac{2}{3}\)of it.

Then I found \(\frac{1}{4}\) of the 8 shaded cells = 2 cells.

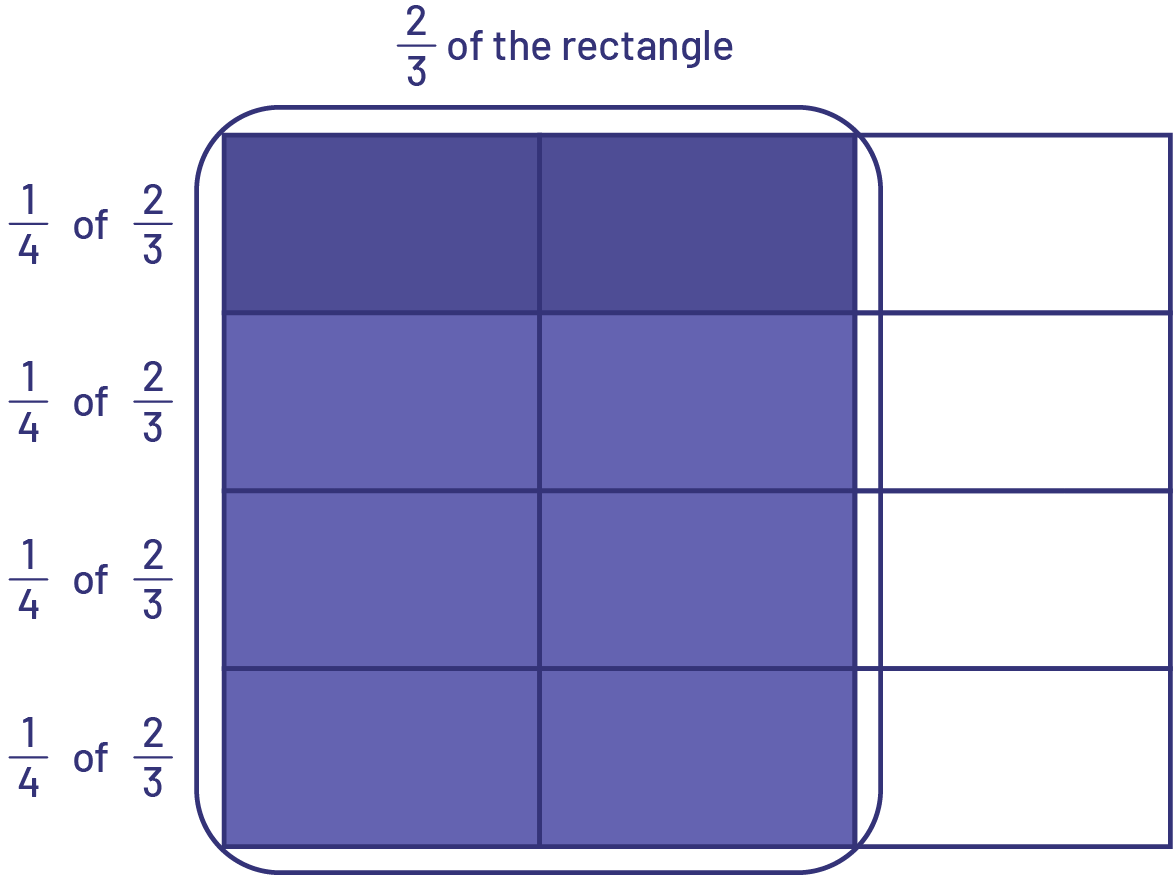
Then, \(\frac{1}{4}\)of \(\frac{2}{3}\)of the rectangle is equal to 2 cells of the set of cells.

\(\frac{1}{4}\;{\rm{of}}\;\frac{2}{3}\;{\rm{of \ rectangle}}\;{\rm{ = }}\;\frac{2}{{12}}\;{\rm{or}}\;\frac{1}{6}\)

Multiplication With Splitting

• Multiplication performed with an area model

\(\frac{3}{4}\; \times \;\frac{2}{3}\) or \(\frac{3}{4}\) of \(\frac{2}{3} \)

Since I am looking for \(\frac{3}{4}\) of \(\frac{2}{3}\), I vertically divided a rectangle into 3 equal parts and coloured 2 parts, which corresponds to \( \frac{2}{3}\) of the rectangle.

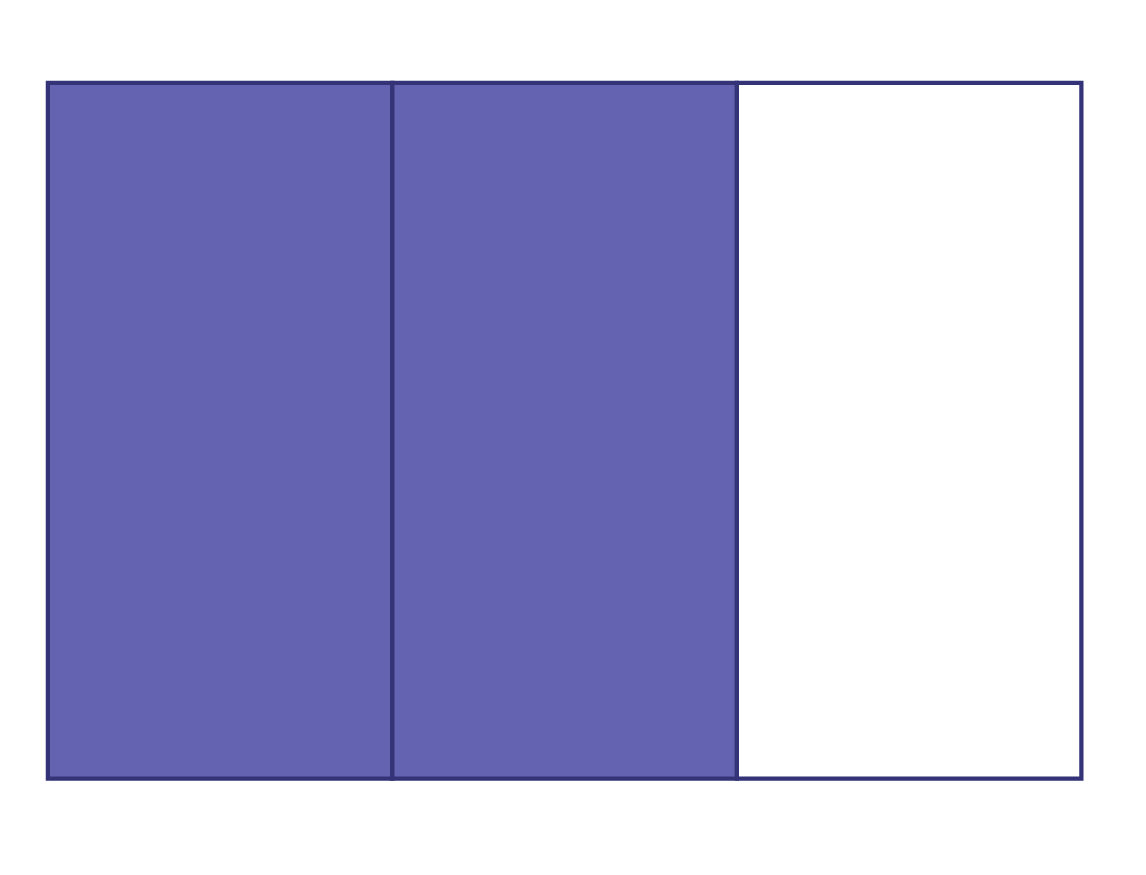
Then I decomposed \(\frac{3}{4}\) into \(\frac{1}{4}\; + \;\frac{1}{4} + \;\frac{1}{ 4}\).

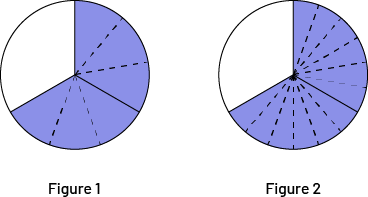
I divided the same rectangle horizontally into 4 equal parts and coloured 1 row, which corresponds to \(\frac{1}{4}\) of the rectangle, or 3 of 12 cells. The fraction that represents \(\frac{1}{4}\) of \(\frac{2}{3}\) corresponds to the number of parts coloured twice, which is \(\frac{2}{{12}}\). The numerator corresponds to the darker coloured parts and the denominator corresponds to the number of parts of the same size in the whole, that is 12 parts (figure 1).

I'm looking for \(\frac{3}{4}\) of \(\frac{2}{3}\), so I can do \(2\; + \;2\; + \;2\) since each \(\frac{1}{4}\) represents 2 cells. So, \(\frac{3}{4}\) represents 6 squares. \(\frac{3}{4}\) of \(\frac{2}{3}\) represents \(\frac{6}{{12}}\) in all (Figure 2). If I move 2 of the squares (Figure 3), I can see that \(\frac{6}{{12}}\) is also \(\frac{1}{2}\).

Multiplying a Fraction by a Whole Number

In Grade 8, students will multiply fractions by whole numbers (for example, \(7\; \times \;\frac{3}{4}\)). In the Primary and Junior Divisions, students recognized the relationship between multiplication and repeated addition. This relationship can also be applied in the case of multiplications of fractions by whole numbers. However, to emphasize multiplication as an operation, it is useful to represent it in various ways. For example, the operation \(4\; \times \;\frac{1}{2}\) which is read "four times one half" can be represented by 4 groups of \(\frac{1}{2 }\)(Figure 1) or using an array (Figure 2).

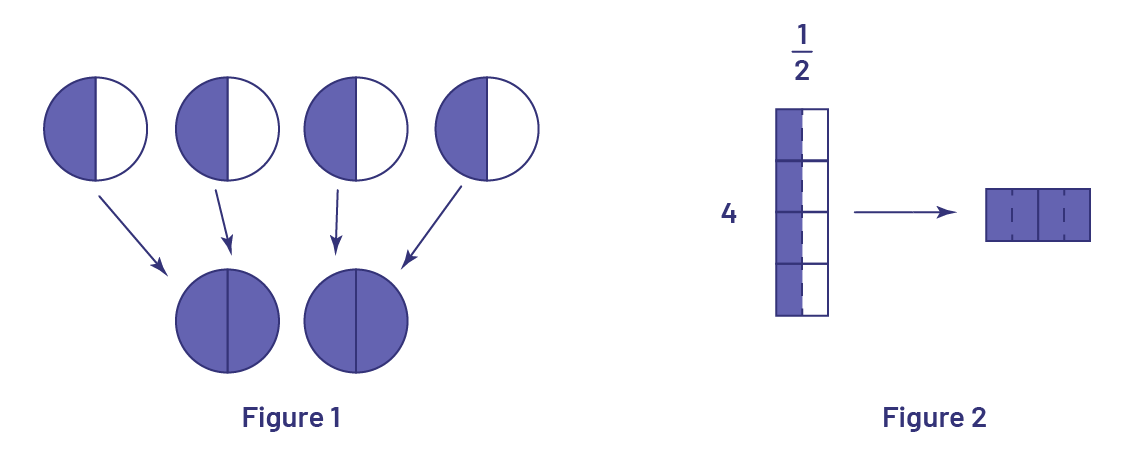
In order to multiply a fraction by a whole number, students develop personal strategies using various models. Consider the following situation:

On an activity day, we want the students to experience six different activities, each lasting three fourths of an hour. How long will all the activities be?

To solve this problem, we can recognize that we can perform the operation \(6\; \times \;\frac{3}{4}\). In order to determine the result, various computational strategies are possible such as:

• perform the repeated addition; \(\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; + \;\frac{3}{4}\; = \;\frac{18}{4}\;{\rm{so}}\; 4\frac{2}{4}\;{\rm{or}}\;4\frac{1}{2}\);

• use a concrete representation;

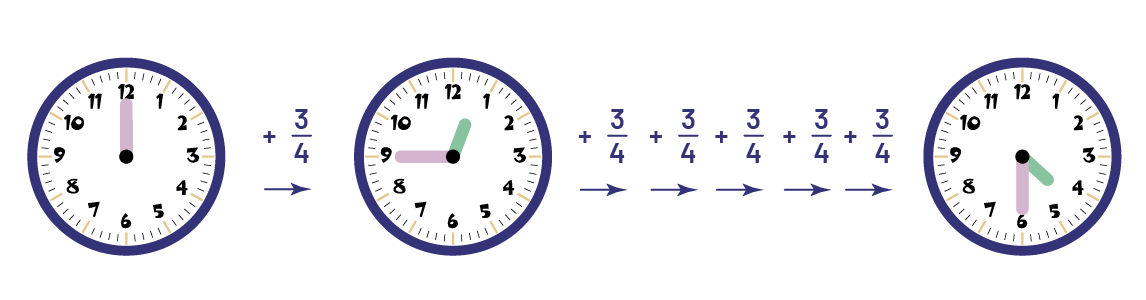
• use a visual representation;

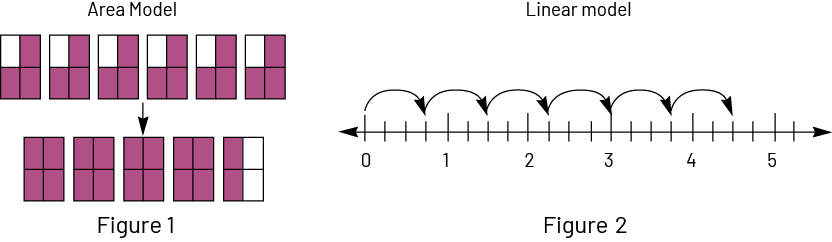
• use an array;

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 95-96.

• perform calculations.

As a result of using various models, some students often notice that they can determine the product using calculations. For example, in order to calculate \(6\; \times \;\frac{3}{4}\), I first multipled 6 by 3, then divided that result by 4 and got \(\frac {{18}}{4}\;{\rm{or}}\;{\rm{4}}\frac{2}{4}\).

This last strategy, although effective, should not be applied without understanding. It is important for students to realize that when they multiply \(6\; \times \;3\), they are determining the number of pieces. Since these pieces are fourths, they then determined that there are a total of 18 fourths (\(\frac{{18}}{4}\)).

Subsequently, when they perform \(18\; \div \;4\), they determine the number of groups of 4 fourths. Thus, they determine that there are 4 wholes and two fourths remain, hence the result \(4\frac{2}{4}\).

Multiplying a Fraction by a Mixed Number

Examples

Note: To calculate the area of a rectangle, multiply the two dimensions, which is equivalent to the area formula.

A = length × width

\(\frac{2}{5}\; \times \;2\frac{1}{4}\;\)

• Multiplication using an area model

I decomposed \(2\frac{1}{4}\) into \(2\; + \;\frac{1}{4}\).

I did the partial multiplications.

I know that \(2\; \times \;\frac{2}{5}\) is the same as \(\frac{2}{5}\; + \;\frac{2}{5} \), which gives me \(\frac{4}{5}\).

To do \(\frac{2}{5}\; \times \;\frac{1}{4}\), I multiplied the numerators together and then multiplied the denominators together. So, \(\frac{2}{5}\; \times \;\frac{1}{4}\; = \;\frac{2}{{20}}\;{\rm{or}} \;\frac{1}{{10}}\).

Now I have to add up the partial products. I found like denominators, which are tenths.

\(\frac{4}{5}\; + \;\frac{1}{{10}}\; = \;\frac{8}{{10}}\; + \frac{1}{{ 10}}\;=\;\frac{9}{{10}}\)

SO, \(\frac{2}{5}\; \times \;2\frac{1}{4}\; = \;\frac{9}{{10}}\).

• Multiplication performed by transforming a mixed number into an improper fraction

I first changed \(2\frac{1}{4}\) into an improper fraction, which is \(\frac{9}{4}\) since \(\frac{4}{4}\; + \;\frac{4}{4}\; + \;\frac{1}{4}\; = \;\frac{9}{4}\).

Now I can multiply the two fractions by multiplying the numerators together and multiplying the denominators together.

\(\begin{array}{c}\frac{2}{5}\; \times \;2\frac{1}{4}\; = \;\frac{2}{5}\; \times \;\frac{9}{4}\\ = \;\frac{{18}}{{20}}\;{\rm{or}}\;\frac{9}{{10}}\end {array}\)

SO, \(\frac{2}{5}\; \times \;2\frac{1}{4}\; = \;\frac{9}{{10}}\).

\(1\frac{1}{3}\; \times \;2\frac{3}{4}\)

• Multiplication using an area model

I decomposed the mixed number \(1\frac{1}{3}\;{\rm{in}}\;{\rm{1}}\;{\rm{ + }}\;\frac{1} {3}\) and \(2\frac{3}{4}\;{\rm{and}}\;{\rm{2}}\;{\rm{ + }}\;\frac{3 }{4}\).

I did the partial multiplications.

\(\begin{align}\left( {1\; + \;\frac{1}{3}} \right) \left( {2\; + \;\frac{3}{4} } \right)\; &= \;\left( {1\; \times \;2} \right)\; + \;\left( {1\; \times \;\frac{3}{4} } \right)\; + \;\left( {2\; \times \;\frac{1}{3}} \right)\; + \;\left( {\frac{1}{3}\; \times \;\frac{3}{4}} \right)\\ &= \;2\; + \;\frac{3}{4}\; + \;\frac{2}{3} \; + \;\frac{3}{{12}}\end{align}\)

I added up all the partial products.

\(\begin{align}2\; + \;\frac{3}{4}\; + \;\frac{2}{3}\; + \;\frac{3}{{12}}\ ; &= \;2\; + \;\frac{9}{{12}}\; + \;\frac{8}{{12}}\; + \;\frac{3}{12}\\ &= \;2\; + \;\frac{{20}}{{12}}\\ &= \;2\; + \;1\frac{8}{{12}}\\ &= \;3\frac{8}{{12}}\;{\rm{ou}}\;{\rm{3}}\frac{2}{3} \\ {\rm{So,} }\; \;1\frac{1}{3} \times \; \;2\frac{3}{4} \; &= \;3\frac{2}{3}\end{align} \)

• Multiplication performed by transforming mixed numbers into improper fractions

I transform the two mixed numbers into improper fractions.

\(1\frac{1}{3}\; = \;\frac{3}{3}\; + \;\frac{1}{3}\; = \;\frac{4}{3} \) \(2\frac{3}{4}\; = \;\frac{4}{4}\; + \;\frac{4}{4}\; + \;\frac{3}{4} \;=\;\frac{11}{4}\)

Now I can multiply the two improper fractions by multiplying the numerators together and multiplying the denominators together.

\(\frac{4}{3}\; \times \;\frac{{11}}{4}\; = \;\frac{44}{12}\; = \;3 \frac{8}{{12}}\;{\rm{or}}\;{\rm{3}}\frac{2}{3}\)

Division

When dividing fractions, there is a certain progression to follow. The exploration of division, like that of other operations, should focus on concrete and visual (semi-concrete) representations and not on algorithms. Students can then reactivate their prior knowledge and grasp the meaning of the operation. In order to understand division, it is essential to examine the meaning of the division and the nature of the numbers that make up the division. Division is partitive when we look for the size of the groups; it is quotative when we look for the number of groups.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 79-80.

Division of a Fraction by a Whole Number

The division of a fraction by a whole number (for example, \(\frac{3}{4}\; \div \;5\)) is more often found in partitive situations. We can start with situations where the numerator is divisible by the divisor (for example, \(\frac{6}{9}\; \div \;3,\;\frac{3}{4}\; \div \;3,\;\frac{4}{9}\; \div \;2,\;\frac{{12}}{{20}}\; \div \;4\)). The examples below show different ways to get the result of dividing \(\frac{6}{9}\;{\rm{by}}\;{\rm{3}}\).

Examples of representations of \(\frac{6}{9}\; \div \;3\; = \;\frac{2}{9}\)

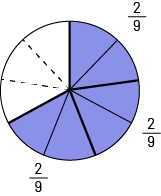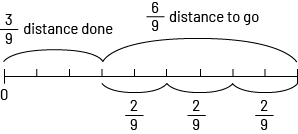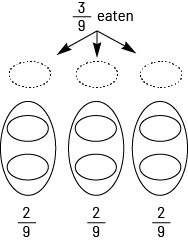Students can then tackle more complex division situations, where the numerator is not divisible by the divisor (for example, \(\frac{2}{3}\; \div \;6, \;\frac{3}{5}\; \div \;12\)).

The complexity comes from the fact that the situation is more difficult to represent. To be successful, it must be understood that partitioning in these situations involves subdividing the parts. The operation is easier to understand when it is presented in context.

Example

The 6 members of a family want to share \(\frac{2}{3}\) of a pie. What fraction of pie will each have?

The question clarifies what one is looking for, that is a fraction of a full pie. Recognizing that division is associated with the concept of partitioning, the situation can be represented symbolically by \(\frac{2}{3}\; \div \;6\). In order to represent the operation, we can illustrate \(\frac{2}{3}\) of a pie.

How do we divide these two thirds? You can divide each third into three equal pieces for a total of six equal pieces (Figure 1). You can also divide the first third into six pieces that will be shared, then do the same with the second third (Figure 2).

In division problems, the main difficulty experienced by students is to find the quantity in relation to the whole. In the previous situation (\(\frac{2}{3}\; \div \;6\)), the fraction \(\frac{2}{3}\) temporarily acts as a whole, because it must be divided into 6. However, the answer must be expressed in relation to the whole to which \(\frac{2}{3}\) refers (the pie). Thus, from the representations above, the student determines that the solution is 1 piece or 2 pieces depending on the division made, but has difficulty in recognizing that it is 1 or 2 pieces of the whole. But how do we know what fraction of the pie each gets? To find out, we must also divide the missing third.

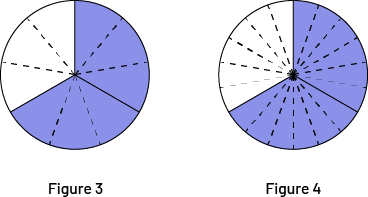
Thus, according to the first split, each receives a piece, or \(\frac{1}{9}\) of a pie (Figure 3). According to the second, each receives two pieces, or \(\frac{2}{{18}}\) of a pie (Figure 4). However, they are the same quantity since \(\frac{1}{9}\) and \(\frac{2}{{18}}\) are equivalent fractions.

Consider the same division (\(\frac{2}{3}\; \div \;6\)) from a situation that relates more to the linear model.

Example

We want to cut \(\frac{2}{3}\) from a piece of rope into 6 sections. What fraction of the rope will each section be?

When we understand the meaning of the problem, we can recognize that we must perform \(\frac{2}{3}\; \div \;6\). In order to determine the quotient, as in the previous example, one can proceed in two ways:

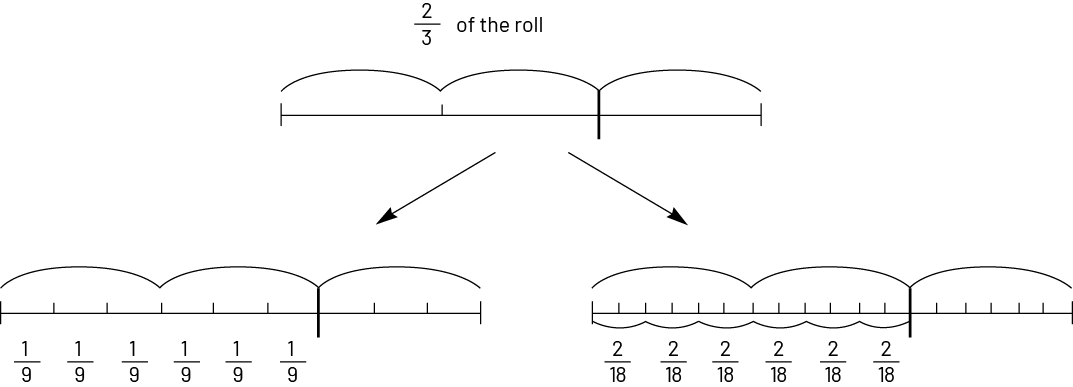
Thus, we can determine that each of the 6 sections corresponds to \(\frac{1}{9}\) or \(\frac{2}{{18}}\) of the piece of rope.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97-100.

Division of a Fraction by a Fraction

Division Without Splitting

Example

\(\frac{5}{6}\; \div \;\frac{1}{6}\)

• Division performed with an area model

I represented \(\frac{5}{6}\) of a rectangle by dividing the rectangle into 6 equal parts and shading 5 parts of them. I asked myself the question «How many \(\frac{1}{6}\) are there in \(\frac{5}{6}\)?»".

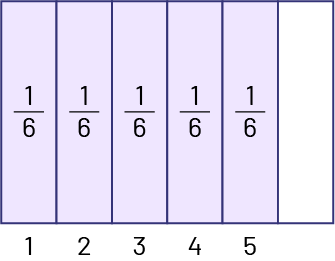
There are 5 one sixths in \(\frac{5}{6}\). So, \(\frac{5}{6}\; \div \;\frac{1}{6}\; = \;5\).

• Division performed with a symbolic representation

Since the dividend and divisor have like denominators, I can divide the numerators and divide the denominators.

\(\frac{5}{6}\; \div \;\frac{1}{6}\; = \;\frac{{5\; \div \;1}}{{6\; \div \;6}}\; = \;\frac{5}{1}\; = \;5\)

Division With Splitting

Example

\(\frac{3}{4}\; \div \;\frac{1}{2}\)

• Division performed using a number line

I represented \(\frac{3}{4}\)on the number line (red line). I ask myself the question «How many groups of \(\frac{1}{2}\) are there in \(\frac{3}{4}\)?».

Knowing that \(\frac{2}{4}\; = \;\frac{1}{2}\), I found how many \(\frac{2}{4}\) there are in \(\frac{3}{4}\).

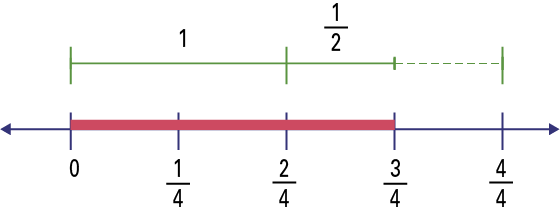
On the number line, I can see that there is one group of \(\frac{1}{2}\) or \(\frac{2}{4}\) and from \(\frac {2}{4}\) to \(\frac{3}{4}\), there is half (\(\frac{1}{2}\)) of another, so in total there are 1\(\frac{1}{2}\) groups of \(\frac{1}{2}\).

• Division performed using like denominators

\(\begin{array}{l}\frac{3}{4}\; \div \;\frac{1}{2}\; = \;\frac{3}{4}\; \div \;\frac{2}{4}\\\quad \quad \;\; = \;\frac{{3\; \div \;2}}{{4\; \div \;4}}\\ \quad \quad \;\; = \;\frac{{\frac{3}{2}}}{1}\; = \;\frac{3}{2}\\\quad \quad \;\;= \;1\frac{1}{2}\end{array}\)

Division of a Fraction by a Mixed Number

Example

\(\frac{7}{{12}}\; \div \;1\frac{3}{4}\)

• Division performed with a symbolic representation

I changed the mixed number into an improper fraction.

\(1\frac{3}{4}\; = \;\frac{4}{4}\; + \;\frac{3}{4}\; = \;\frac{7}{4} \)

Possible answer 1: "I divided the numerators and denominators.

\(\frac{7}{{12}}\; \div \;\frac{7}{4}\; = \;\frac{{7\; \div \;7}}{{12\; \div \;4}}\;=\;\frac{1}{3}\)

So, \(\frac{7}{{12}}\; \div \;1\frac{3}{4}\; = \;\frac{1}{3}\)

Possible answer 2: "I found like denominators and then divided.

\(\frac{7}{{12}}\; \div \;\frac{7}{4}\; = \;\frac{7}{{12}}\; \div \;\frac{ {21}}{{12}}\;=\;\frac{{\frac{7}{{21}}}}{1}\;=\;\frac{7}{{21}}\; {\rm{or}}\;\frac{1}{3}\)

So, \(\frac{7}{{12}}\; \div \;1\frac{3}{4}\; = \;\frac{1}{3}\)

Knowledge: Fractions

---

The word fraction comes from the Latin fractio which means "break". In order to determine a fraction of a whole that has been divided into parts, the parts must be of equal or equivalent size.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 33.

Knowledge: Numerator

---

Number of equal parts into which a whole or set is divided.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.

Knowledge: Denominator

---

Number of equivalent parts by which the whole is divided.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.

Knowledge: Fractional Notation

---

The fractional notation \(\frac{a}{b}\) is usually associated with the concept of part of a whole. The whole can be an element or a set of elements.

Example

• I gave 1 fourth (\(\frac{1}{4}\)) of my sandwich to Alex.

• A fourth (\(\frac{1}{4}\)) of my marbles are blue.

However, fractional notation can also be associated with other concepts such as division, ratio and operator.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.