B2.7 Multiplier et diviser des nombres entiers, à l’aide de stratégies appropriées, dans divers contextes.
Habileté : multiplier et diviser des nombres entiers, à l’aide de stratégies appropriées, dans divers contextes
L’élève de 8e année multiplie et divise des nombres entiers en utilisant différentes représentations (jetons bicolores, droite numérique, suites) et des stratégies de calcul qui lui permettront de généraliser des règles de calcul.
L’utilisation de jetons bicolores et de la droite numérique est essentielle pour illustrer la multiplication et la division de nombres entiers. En utilisant ces modèles, l’élève se crée des représentations visuelles des opérations à effectuer et peut mieux comprendre la raison d’être des différentes règles qui régissent la multiplication et la division des nombres entiers. Plutôt que d’enseigner des règles, il est préférable que l’élève, à la suite de certaines observations, puisse les généraliser. Les règles de calcul concernant les nombres entiers constituent le point d’arrivée et non le point de départ de l’enseignement et de l’apprentissage de ces nombres.
Source : Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e année, Module 3, Série 1, Introduction, p. 15.
Multiplication
Certaines règles de la multiplication de nombres naturels, de fractions et de nombres décimaux s’apprêtent aux nombres entiers. Cependant, l’élève découvrira que les signes des nombres entiers exercent une influence sur le signe du produit.
Source : inspiré du CFORP, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e année, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 87.
Exemples
Légende :

\(3\; \times \;2\)
Représentations à l’aide de diverses conventions : \(( 3)( 2)\); \(( 3) \cdot ( 2)\)
Représentation à l’aide de mots : 3 groupes de 2
Représentation à l’aide de jetons bicolores :

Représentation à l’aide d’une droite numérique :
 Image Une droite numérique est graduée de moins six à six.
Au-dessus de la droite, une flèche relie zéro à deux en indiquant deux. Une flèche relie deux à quatre en indiquant
deux. Et une flèche relie quatre à six en indiquant deux.
Image Une droite numérique est graduée de moins six à six.
Au-dessus de la droite, une flèche relie zéro à deux en indiquant deux. Une flèche relie deux à quatre en indiquant
deux. Et une flèche relie quatre à six en indiquant deux.
Représentation symbolique : \(3\; \times \;2\; = \;6\;{\rm{ou}}\;{\rm{2}}\;{\rm{ + }}\;{\rm{2}}\;{\rm{ + }}\;{\rm{2}}\;{\rm{ = }}\;{\rm{6}}\)
\(3\; \times \; (- 2)\)
Représentations à l’aide de diverses conventions : \(( 3)(- 2)\); \(( 3) \cdot (- 2)\)
Représentation à l’aide de mots : 3 groupes de \((- 2)\)
Représentation à l’aide de jetons bicolores :

Représentation à l’aide d’une droite numérique :
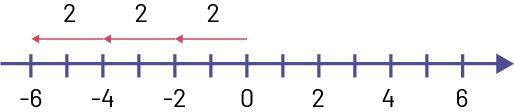 Image Une droite numérique est graduée de moins six à six.
Au-dessus de la droite, une flèche relie zéro à moins deux en indiquant deux. Une flèche relie moins deux à moins
quatre en indiquant deux. Et une flèche relie moins quatre à moins six en indiquant deux.
Image Une droite numérique est graduée de moins six à six.
Au-dessus de la droite, une flèche relie zéro à moins deux en indiquant deux. Une flèche relie moins deux à moins
quatre en indiquant deux. Et une flèche relie moins quatre à moins six en indiquant deux.
Représentation symbolique : \(3\; \times (- 2)\; = \;(- 6)\;{\rm{ou}}\; (- 2)\; + \; (- 2)\; + (- 2)\; = \; (- 6)\)
\( (- 3)\; \times \;2\)
L’élève peut utiliser la propriété de la commutativité et effectuer \(2\; \times (- 3)\), ce qui donne la même réponse.
Représentations à l’aide de diverses conventions : \((- 3)( 2)\); \((- 3) \cdot ( 2)\)
Représentation à l’aide de mots : l’opposé de 3 groupes de 2
Représentation à l’aide de jetons bicolores :
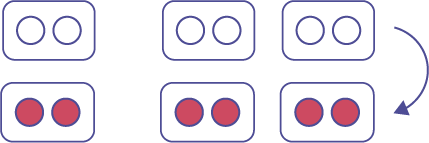
Représentation à l’aide d’une droite numérique :
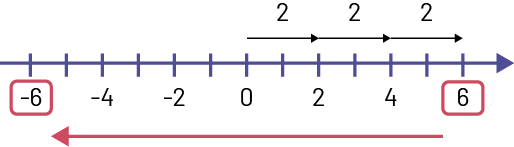 Image Une droite numérique est graduée de moins six à six.
Au-dessus de la droite, une flèche relie zéro à moins deux en indiquant deux. Une flèche relie moins deux à moins
quatre en indiquant deux. Et une flèche relie moins quatre à moins six en indiquant deux.
Image Une droite numérique est graduée de moins six à six.
Au-dessus de la droite, une flèche relie zéro à moins deux en indiquant deux. Une flèche relie moins deux à moins
quatre en indiquant deux. Et une flèche relie moins quatre à moins six en indiquant deux.
Représentation symbolique : \( (- 3)\; \times \;2\; = (- 6)\)
\( (- 3)\; \times \; (- 2)\)
Représentations à l’aide de diverses conventions : \((- 3)( - 2)\); \((- 3) \cdot (- 2)\)
Représentation à l’aide de mots : l’opposé de 3 groupes de \( (- 2)\)
Représentation à l’aide de jetons bicolores :
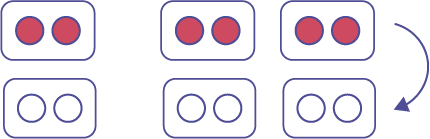
Représentation à l’aide d’une droite numérique :
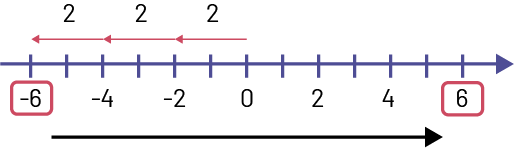 Image
Une droite numérique est graduée de moins six à six. Au-dessus de la droite, une flèche relie zéro à moins deux en
indiquant deux. Une flèche relie moins deux à moins quatre en indiquant deux. Et une flèche relie moins quatre à moins
six en indiquant deux.Moins six et six sont encadrés en rouge, et une flèche noire relie le premier au deuxième.
Image
Une droite numérique est graduée de moins six à six. Au-dessus de la droite, une flèche relie zéro à moins deux en
indiquant deux. Une flèche relie moins deux à moins quatre en indiquant deux. Et une flèche relie moins quatre à moins
six en indiquant deux.Moins six et six sont encadrés en rouge, et une flèche noire relie le premier au deuxième.
Représentation à l’aide d’une régularité :
 Image Quatre multiplications sont présentées l’une sous l’autre. Première multiplication : zéro fois
deux égale
zéro. Deuxième multiplication : moins un fois moins deux égale deux. Une flèche relie le facteur zéro de la
première
multiplication au facteur moins un de la deuxième en indiquant moins un. Une flèche relie le produit zéro de la
première multiplication au produit deux de la deuxième en indiquant plus deux. Troisième multiplication : moins
deux fois moins deux égale quatre. Une flèche relie le facteur moins deux de la
troisième en indiquant moins un. Une flèche relie le produit deux de la deuxième multiplication au produit quatre
de la troisième en indiquant plus deux. Quatrième multiplication, encadrée : moins trois fois moins deux égale
six. Une flèche relie le facteur moins
deux de la troisième multiplication au facteur moins trois de la quatrième en indiquant moins un. Une flèche relie
le produit quatre de la troisième multiplication au produit six de la quatrième en indiquant plus deux. Un encadré
textuel dit : Lorsque le premier facteur diminue d’un, le produit augmente de moins deux de moins qui
fait diminuer le produit. Pour prolonger la suite, les produits doivent être positifs
Image Quatre multiplications sont présentées l’une sous l’autre. Première multiplication : zéro fois
deux égale
zéro. Deuxième multiplication : moins un fois moins deux égale deux. Une flèche relie le facteur zéro de la
première
multiplication au facteur moins un de la deuxième en indiquant moins un. Une flèche relie le produit zéro de la
première multiplication au produit deux de la deuxième en indiquant plus deux. Troisième multiplication : moins
deux fois moins deux égale quatre. Une flèche relie le facteur moins deux de la
troisième en indiquant moins un. Une flèche relie le produit deux de la deuxième multiplication au produit quatre
de la troisième en indiquant plus deux. Quatrième multiplication, encadrée : moins trois fois moins deux égale
six. Une flèche relie le facteur moins
deux de la troisième multiplication au facteur moins trois de la quatrième en indiquant moins un. Une flèche relie
le produit quatre de la troisième multiplication au produit six de la quatrième en indiquant plus deux. Un encadré
textuel dit : Lorsque le premier facteur diminue d’un, le produit augmente de moins deux de moins qui
fait diminuer le produit. Pour prolonger la suite, les produits doivent être positifs
Représentation symbolique : -3 × -2 = 6
Source : Grandes idées pour l’enseignement des mathématiques – 9 à 14 ans, Marian Small, p. 102.
Source : inspiré du CFORP, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e année, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 95
Certaines généralisations que l’élève peut faire :
- Il y a des conventions pour exprimer la multiplication de manière à rendre les expressions algébriques plus claires.
- Un entier positif multiplié par un entier positif a un résultat positif.
- Un entier positif multiplié par un entier négatif a un résultat négatif.
- Un entier négatif multiplié par un entier positif a le même résultat qu’un entier positif multiplié par un entier négatif puisque la propriété de la commutativité s’applique à la multiplication de nombres entiers.
- Lorsque le premier facteur est positif, il peut représenter le nombre de groupes et l’autre entier positif ou négatif peut représenter la quantité dans chaque groupe.
- La multiplication de nombres entiers peut être vue comme une addition répétée puisqu’elle contient des groupes égaux répétés.
- Des régularités peuvent être utilisées pour déterminer qu’un entier négatif multiplié par un entier négatif a un résultat positif. Si on prend l’exemple de \( (- 3)\; \times (- 2)\), lorsque le premier facteur diminue de 1, le produit augmente de (-2) de moins qui fait diminuer le produit. Pour prolonger la suite, les produits doivent être positifs.
Source: inspiré de Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
- Lorsque l’entier est négatif, on peut dire que c’est l’opposé de l’entier positif (par exemple, (-3) est l’opposé de 3).
- Un tableau synthèse :
| x | Entier positif | Entier négatif |
|---|---|---|
| Entier positif | Produit positif | Produit négatif |
| Entier négatif | Produit négatif | Produit positif |
Source : inspiré du CFORP, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e année, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 91
Division
Certaines règles de la division de nombres naturels, de fractions et de nombres décimaux s’apprêtent aux nombres entiers. Cependant, l’élève découvrira que les signes des nombres entiers exercent une influence sur le signe du quotient.
Source : adapté du CFORP, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e année, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 87.
La compréhension de la division des nombres entiers requiert une compréhension approfondie de cette opération et de sa relation avec la multiplication.
Source : adapté du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemples
Légende :

\(6\; \div \;2\;\)
Représentations à l’aide du symbole de division ou de la notation fractionnaire : \(6\; \div \;(^+ 2)\); \(\frac{6}{2}\;{\rm{ou}}\;\frac{6}{^+2}\)
Représentation à l’aide de mots :
- Groupement : Combien de groupes de 2 se trouvent dans 6?
- Partage : Combien chacun en reçoit-il si 6 (biscuits) sont partagés entre 2 (personnes)?
Représentation à l’aide de jetons bicolores (groupement) :

Représentation à l’aide d’une droite numérique (groupement) :

Représentation à l’aide d’une multiplication comme opération inverse : \(2\; \times \;?\; = \;6\)
Représentation symbolique : \(6\; \div \;2\; = \;3\)
\(6\; \div \; (- 2)\;\)
Représentations à l’aide du symbole de division ou de la notation fractionnaire : \(6\; \div \;(- 2)\); \(\frac{6}{{^-2}}\;\)
Utiliser la relation inverse entre la multiplication et la division pour réécrire cet énoncé comme \(\left( {- 2} \right)\; \times \;?\; = \;\left( {+6} \right)\).
Représentation à l’aide de jetons bicolores :
L’opposé de deux groupes de 3 jetons blancs
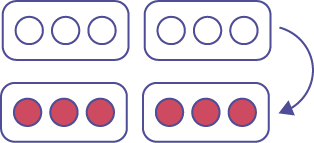
Représentation à l’aide d’une droite numérique :
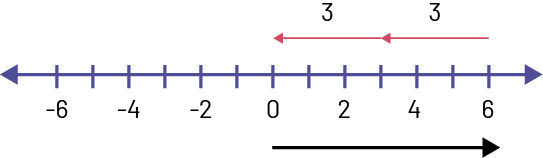 Image Une double droite numérique est graduée de moins six à
six. Au-dessus de la droite, une flèche relie trois à zéro en indiquant trois. Et une flèche relie six à trois en
indiquant trois. Sous la droite, une flèche part de zéro et se rend à six.
Image Une double droite numérique est graduée de moins six à
six. Au-dessus de la droite, une flèche relie trois à zéro en indiquant trois. Et une flèche relie six à trois en
indiquant trois. Sous la droite, une flèche part de zéro et se rend à six.
Représentation à l’aide d’une multiplication comme opération inverse : \( (- 2)\; \times \;?\; = \;6\;{\rm{ou}}\;{\rm{?}}\; \times \; (- 2)\; = \;6\)
Représentation symbolique : \(6\; \div \; (- 2)\; = \; (- 3)\)
\( (- 6)\; \div \;2\;\)
Représentations à l’aide du symbole de division ou de la notation fractionnaire : \(( - 6)\; \div \;( 2)\); \(\frac{{- 6}}{2}\;{\rm{ou}}\;\frac{{- 6}}{^+2}\)
Représentation à l’aide de mots :
- Partage : Combien chacun en reçoit-il si 6 jetons rouges (-6) est partagé en 2 groupes?
Représentation à l’aide de jetons bicolores :

Représentation à l’aide d’une droite numérique :
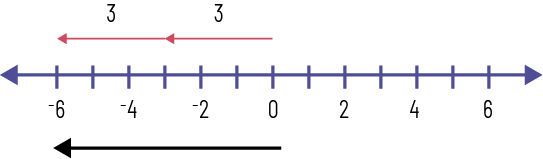 Image
Une double droite numérique est graduée de moins six à six. Au-dessus de la droite, une flèche relie zéro à moins
trois en indiquant trois. Et une flèche relie moins trois à moins six en indiquant trois. Sous la droite, une flèche
part de zéro et se rend à moins six.
Image
Une double droite numérique est graduée de moins six à six. Au-dessus de la droite, une flèche relie zéro à moins
trois en indiquant trois. Et une flèche relie moins trois à moins six en indiquant trois. Sous la droite, une flèche
part de zéro et se rend à moins six.
Représentation à l’aide d’une multiplication comme opération inverse : \(2\; \times \;?\; = \; (- 6)\)
Représentation symbolique : \( (- 6)\; \div \;2\; = \; (- 3)\)
\( (- 6)\; \div \; (- 2)\;\)
Représentations à l’aide du symbole de division ou de la notation fractionnaire : \((- 6)\; \div \;( - 2)\); \(\frac{{- 6}}{{- 2}}\;\)
Représentation à l’aide de mots :
- Partage : Combien de groupes de (-2) se trouvent dans (-6)?
Représentation à l’aide de jetons bicolores (groupement) :
L’opposé de deux groupes de 3 jetons rouges
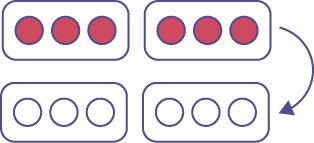
Représentation à l’aide d’une droite numérique :
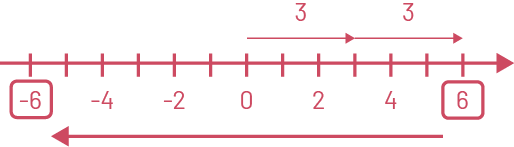 Image Une
double droite numérique est graduée de moins cinq à dix.
Au-dessus de la droite, une flèche relie deux à zéro en indiquant deux. Une flèche relie quatre à deux en indiquant
deux. Et une flèche relie six à quatre en indiquant deux. Sous la droite, une flèche part de zéro et se rend à six.
Image Une
double droite numérique est graduée de moins cinq à dix.
Au-dessus de la droite, une flèche relie deux à zéro en indiquant deux. Une flèche relie quatre à deux en indiquant
deux. Et une flèche relie six à quatre en indiquant deux. Sous la droite, une flèche part de zéro et se rend à six.
Représentation à l’aide d’une multiplication comme opération inverse : \( (-2)\; \times \;?\; = \; (- 6)\;\;\;{\rm{ou}}\;\;\;{\rm{?}}\; \times \; (- 2)\; = \; (- 6)\)
Représentation symbolique : \( (- 6)\; \div \; (- 2)\; = \;3\)
Certaines généralisations que l’élève peut faire :
- Un nombre entier positif divisé par un nombre entier positif donne un résultat positif.
- Un nombre entier positif divisé par un nombre entier négatif donne un résultat négatif.
- Un nombre entier négatif divisé par un nombre entier positif donne un résultat négatif.
- Un nombre entier négatif divisé par un nombre entier négatif donne un résultat positif.
Source : adapté du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
- Lorsque l’entier est négatif, on peut dire que c’est l’opposé de l’entier positif (par exemple, (-3) est l’opposé de 3).
Un tableau synthèse :
| ÷ | Entier positif | Entier négatif |
|---|---|---|
| Entier positif | Quotient positif | Quotient négatif |
| Entier négatif | Quotient négatif | Quotient positif |
Source : adapté du CFORP, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e année, Module 3, Série 1, Activité 5 Divisons, p. 109.
Connaissance: nombres entiers
Les nombres entiers appartiennent à l’ensemble \(\mathbb{Z}\).
\(\mathbb{Z}\)= {…, –3, –2, –1, 0, 1, 2, 3…}
Chaque nombre entier est formé d’un nombre et d’un signe (– ou +).
Chaque nombre entier a un opposé (par exemple, (–3) et 3). L’opposé d’un nombre positif est un nombre négatif de même quantité (valeur absolue), et vice versa.
Les signes + et – sont associés au nombre. Ce ne sont pas des signes d’opération. Ainsi, le nombre (–4) se lit : l’opposé de 4 ou négatif 4.
Il n’y a pas d’espace entre le signe négatif (–) et le nombre 4, puisqu’il ne s’agit pas de l’opération de soustraction.
Zéro n’est ni un nombre positif ni un nombre négatif, car il est le seul nombre à être son propre opposé.
Sur la droite numérique, les nombres sont par ordre croissant de la gauche vers la droite et par ordre décroissant de la droite vers la gauche.

Source : adapté du CFORP, Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 7e année, Module 3, Série 1, Activité 1 Des nombres entiers sur la droite numérique, p. 35-37.
