B2.7 Multiply and divide integers, using appropriate strategies, in various contexts.
Skill: Multiplying and Dividing Integers, Using Appropriate Strategies, in Various Contexts
Grade 8 students will multiply and divide integers using a variety of representations (two-coloured counters, number line, patterns) and computational strategies that will allow them to generalize computational rules.
The use of two-coloured counters and the number line is essential for illustrating integer multiplication and division. By using these models, the students create visual representations of the operations to be performed and can therefore better understand the rationale for the different rules that govern integer multiplication and division. Rather than teaching rules, it is better for the student to be able to generalize them as a result of some observations. The rules for integer computation are the end point, not the beginning point, of teaching and learning about integers.
Source: translated from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 8e, Module 3, Série 1, Introduction, p. 15.
Multiplication
Some of the rules for multiplication of whole numbers, fractions, and decimals are appropriate for integers. However, the student will discover that the signs of integers influence the sign of the product.
Source: inspired by and translated from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 8e, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 87.
Examples
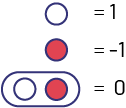
Key:
White circle: positive one
Red circle: negative one
White circle plus red circle: 0 (zero pair)

\(3\; \times \;2\)
Representations using various conventions: \(( + 3)( + 2)\); \(( + 3) \cdot ( + 2)\)
Representation using words: 3 groups of 2
Representation using two-coloured counters, with three copies of \(( + 2)\):

Representation using a number line:

Symbolic representation: \(3\; \times \;2\; = \;6\;{\rm{or}}\;{2}\;{\rm{ + }}\;{\rm{2}}\;{\rm{ + }}\;{\rm{2}}\;{\rm{ = }}\;{\rm{6}}\)
\(3\; \times \; - 2\)
Representations using various conventions: \(( + 3)( - 2)\); \(( + 3) \cdot ( - 2)\)
Representation using words: 3 groups of \( - 2\)
Representation using two-coloured counters, with three copies of \(( - 2)\):

Representation using a number line:
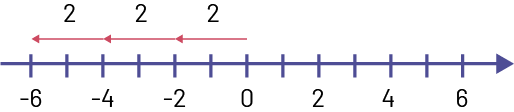
Symbolic representation: \(3\; \times \; - 2\; = \; - 6\) or \(- 2\; + \; - 2\; + - 2\; = \; - 6\)
\( - 3\; \times \;2\)
The student can use the commutative property and perform \(-2\; \times \; 3\), which gives the same answer.
Representations using various conventions: \(( - 3)( + 2)\); \(( - 3) \cdot ( + 2)\)
Representation using words: the opposite of 3 groups of 2
Representation using two-coloured counters:
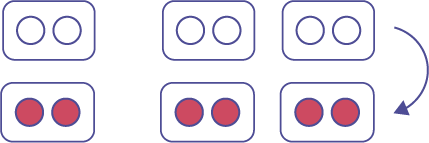
Representation using a number line:

Symbolic representation: \( - 3\; \times \;2\; = \; - 6\)
\( - 3\; \times \; - 2\)
Representations using various conventions: \(( - 3)( - 2)\); \(( - 3) \cdot ( - 2)\)
Representation using two-coloured counters, by removing 3 copies of \( + 2\) from zero pairs:
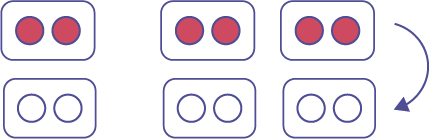
Representation using a number line:
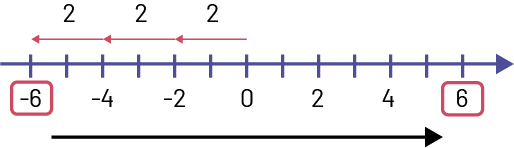
Representation using a pattern:

Source: translated from Grandes idées pour l’enseignement des mathématiques – 9 à 14 ans, Marian Small, p. 102.
Source: adapted and translated from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 8e, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 95
Some generalizations the students can make:
- There are conventions for expressing multiplication to make algebraic expressions clearer.
- A positive integer multiplied by a positive integer has a result that is positive.
- A positive integer multiplied by a negative integer has a result that is negative.
- A negative integer multiplied by a positive integer has the same result as a positive integer multiplied by a negative integer since the commutative property applies to the multiplication of integers.
- When the first factor is positive, it can represent the number of groups and the other positive or negative integer can represent the size of the group.
- Integer multiplication can be seen as repeated addition since it contains repeated equal groups.
- Patterns can be used to determine that a negative integer multiplied by a negative integer has a positive result. If we take the example of \( - 3\; \times \; - 2\), when the first factor decreases by 1, the product increases by (-2). To extend the pattern, the products must be positive.
Source: adapted from Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
- When the integer is negative, we can say that it is the opposite of the positive integer (for example, -3 is the opposite of 3).
- A summary table:
| x | Positive integer | Negative integer |
|---|---|---|
| Positive integer | Positive product | Negative product |
| Negative integer | Negative product | Positive product |
Source: inspired by and translated from Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 8e, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 91
Division
Some of the rules for dividing whole numbers, fractions and decimals are appropriate for whole numbers. However, the student will discover that the signs of integers influence the sign of the quotient.
Source: adapted from CFORP, Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 8e, Module 3, Série 1, Activité 4 Multiplication de nombres entiers, p. 87.
Understanding division of integers requires a strong understanding of the operation and its relationship to multiplication.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Examples
Key:
White circle: positive one
Red circle: negative one
White circle plus red circle: 0
\(6\; \div \;2\;\)
Representations using division sign or fractional notation: \(6\; \div \;( + 2)\); \(\frac{6}{2}\;{\rm{or}}\;\frac{6}{{ + 2}}\)
Representation using words:
- Quotative: How many groups of 2 are in 6? (this size of group is known)
- Partitive: How much does each person get if 6 (cookies) are shared between 2 (people)? (the number of groups is known)
Representation using two-coloured counters (partitive), by dividing six white counters into two equal groups:

Representation using a number line (partitive):

Representation using a multiplication as the inverse operation: \(2\; \times \;?\; = \;6\)
Symbolic representation: \(6\; \div \;2\; = \;3\)
\(6\; \div \; - 2\;\)
Representations using division sign or fractional notation: \(6\; \div \;( - 2)\); \(\frac{6}{{ - 2}}\;\)
Use the inverse relationship between multiplication and division to rewrite this statement as \((- 2)\; \times \;?\; = (+ 6) \).
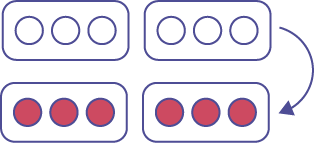
Representation using two-coloured counters, using multiplicative comparison, where two groups of three red counters match the six white counters and are opposite, so equals \(-2\):
The opposite of two groups of 3 white counters is two groups of red counters \((-2)\).
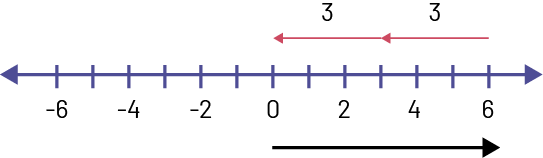
Representation using a number line:
Representation using a multiplication as an inverse operation: \( - 2\; \times \;?\; = \;6\;{\rm{or}}\;{\rm{?} }\; \times \; - 2\; = \;6\)
Symbolic representation: \(6\; \div \; - 2\; = \; - 3\)
\( - 6\; \div \;2\;\)
Representations using division sign or fractional notation: \(( - 6)\; \div \;( + 2)\); \(\frac{{ - 6}}{2}\;{\rm{or}}\;\frac{{ - 6}}{{ + 2}}\)
Representation using words:
- Partitive: How much does each person get if 6 red counters (-6) are shared into 2 groups?
Representation using two-coloured counters, by dividing six red counters into two groups:

Representation using a number line:

Representation using multiplication as an inverse operation: \(2\; \times \;?\; = \; - 6\)
Symbolic representation: \( - 6\; \div \;2\; = \; - 3\)
\( - 6\; \div \; - 2\;\)
Representations using division sign or fractional notation: \(( - 6)\; \div \;( - 2)\); \(\frac{{ - 6}}{{ - 2}}\;\)
Representation using words:
- Quotative: How many groups of (-2) are in (-6)?
Representation using two-coloured counters, using multiplicative comparison, where three groups of two red counters match the six white counters:

Representation using a number line:

Representation using a multiplication as an inverse operation: \( - 2\; \times \;?\; = \; - 6\;{\rm{or}}\;{\ rm{?}}\; \times \; - 2\; = \; - 6\)
Symbolic representation: \( - 6\; \div \; - 2\; = \;3\)
Some generalizations the students can make:
- A positive number divided by a positive number has a result that is positive.
- A positive number divided by a negative number has a result that is negative.
- A negative number divided by a positive number has a result that is negative.
- A negative number divided by a negative number has a result that is positive.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
- When the integer is negative, we can say that it is the opposite of the positive integer (for example, -3 is the opposite of 3).
- A summary table:
| ÷ | Positive integer | Negative integer |
|---|---|---|
| Positive integer | Positive quotient | Negative quotient |
| Negative integer | Negative quotient | Positive quotient |
Source: adapted and translated from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 8e, Module 3, Série 1, Activité 5 - Divisons, p. 109.
Knowledge: Integers
The integers belong to the set \(\mathbb{I}\).
\(\mathbb{I}\)= {…, –3, –2, –1, 0, 1, 2, 3…}
Each integer is formed by a number and a sign (- or +).
Every integer has an opposite (for example, -3 and 3). The opposite of a positive number is a negative number of the same quantity (absolute value), and vice versa.
The signs - and + are associated with number. They are not operation signs. Thus, the number -4 reads: the opposite of 4 or negative 4.
There is no space between the negative sign - and the number 4, since it is not the subtraction operation.
Zero is neither a positive nor a negative number, because it is the only number that is its own opposite.
On the number line, the numbers are in ascending order from left to right and descending order from right to left.

Source: adapted from CFORP, Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 7e, Module 3, Série 1, Activité 1 Des nombres entiers sur la droite numérique, p. 35-37.
