B2.8 Comparer des situations proportionnelles et déterminer la valeur de l’inconnue dans des situations proportionnelles, et utiliser le raisonnement proportionnel pour résoudre des problèmes, dans divers contextes.
Habileté : utiliser le raisonnement proportionnel pour identifier des situations proportionnelles et non proportionnelles
La capacité de maîtriser le raisonnement proportionnel est un facteur déterminant pour la compréhension et l’application des mathématiques. Lamon estime que plus de 90 % des élèves admis à l’école secondaire ne possèdent pas les capacités de raisonnement nécessaires pour bien comprendre les mathématiques et les sciences, et sont mal préparés pour les applications concrètes en statistique, en biologie, en géographie ou en physique (Lamon, 2005, p. 10). L’élève est peut-être capable de résoudre un problème fondé sur les proportions selon une méthode qui a été mémorisée, mais cela ne signifie pas pour autant que l’élève soit capable d’appliquer un raisonnement proportionnel au cours de la résolution de ce problème.
Source : Qu’est-ce que le raisonnement proportionnel?, p. 4.
Raisonnement multiplicatif
C’est un concept qui exige la capacité de traiter plusieurs idées ou quantités à la fois. L’idée est de voir les problèmes selon des valeurs relatives plutôt qu’absolues. Examinons le problème suivant : « Si le poids d’un chien passe de 5 kg à 8 kg et que celui d’un autre chien passe de 3 kg à 6 kg, quel est le chien qui a le plus engraissé? » Si l’élève aborde le problème du point de vue des valeurs absolues ou des additions, elle ou il peut avoir tendance à répondre que les deux chiens ont pris autant de poids. Cependant, en se basant sur les valeurs relatives, l’élève peut affirmer que le deuxième chien a plus engraissé puisqu’il a doublé son poids de départ contrairement au premier, qui aurait dû atteindre 10 kg pour que sa prise de poids relative soit équivalente. Le tableau suivant illustre de manière visuelle les deux réponses de ce problème. S’il est vrai que les deux réponses peuvent se défendre, c’est sur la valeur relative (raisonnement multiplicatif) qu’il faut se baser pour appliquer un raisonnement proportionnel.
| Représentation du raisonnement basé sur des valeurs absolues | Représentation du raisonnement basé sur des valeurs relatives |
|---|---|
|
Le premier chien a pris 3 kg et le deuxième aussi. Ils ont pris autant de poids l’un que l’autre. 1er chien 
2e chien 
|
Le deuxième chien a engraissé davantage puisqu’il a doublé son poids, tandis que le
premier aurait dû atteindre 10 kg pur un gain de poids relativement équivalent. 1er chien 
A moins que doublé son poids 2e chien 
A doublé son poids
|
Pourquoi est-ce important?
Il est difficile d’amener l’élève à passer d’un raisonnement additif à un raisonnement multiplicatif, d’où l’importance de débuter à un jeune âge. C’est la base même du programme-cadre de mathématiques de l’Ontario, de la 1re à la 8e année, qui comprend des idées importantes reliées entre elles comme la multiplication, la division, les fractions, les décimales, les rapports, les pourcentages et les fonctions linéaires. Il faut du temps, diverses situations d’apprentissage et toutes sortes d’occasions pour acquérir des connaissances de différentes façons.
Source : Qu’est-ce que le raisonnement proportionnel?, p. 5-6.
Les relations de proportionnalité
Il y a une relation de proportionnalité entre deux quantités lorsque ces quantités peuvent augmenter ou diminuer simultanément selon le même facteur. Par exemple, si une des deux quantités est triplée, l’autre est triplée aussi. Le rapport entre les deux quantités est alors constant (par exemple, \(\frac{1}{6}\; = \;\frac{3}{{18}}\)). Une telle égalité entre deux rapports s’appelle une proportion.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 39.
Exemple 1
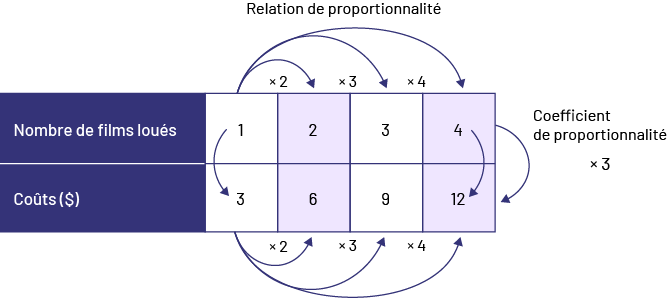Image Le tableau s’intitule Relation de proportionnalité. Chaque thème
possède quatre cases contenant toutes un
chiffre. Le thème Nombre de films loués présente les chiffres un, deux, trois, quatre. Une flèche relie un à deux en
indiquant fois deux. Une flèche relie un à trois en indiquant fois trois. Et une flèche relie un à quatre en
indiquant fois quatre. Le thème Coûts en dollars présente les chiffres trois, six, neuf, douze. Une flèche relie
trois à six en indiquant fois deux. Une flèche relie trois à neuf en indiquant fois trois. Et une flèche relie trois
à douze en indiquant fois quatre. Il y a également une flèche qui relie le chiffre un du premier thème au chiffre
trois du deuxième thème, et une
autre qui relie le chiffre trois du premier thème au chiffre neuf du deuxième thème. Enfin, une flèche relie le
premier thème au deuxième en indiquant Coefficient de proportionnalité fois trois.
Exemple 2
Un aquarium, vide au départ, se remplit à raison de 2 litres d’eau par minute. Représente, de plusieurs façons, le nombre de litres d’eau dans l’aquarium en fonction du temps, en minutes.
Représentation visuelle (table de valeurs)
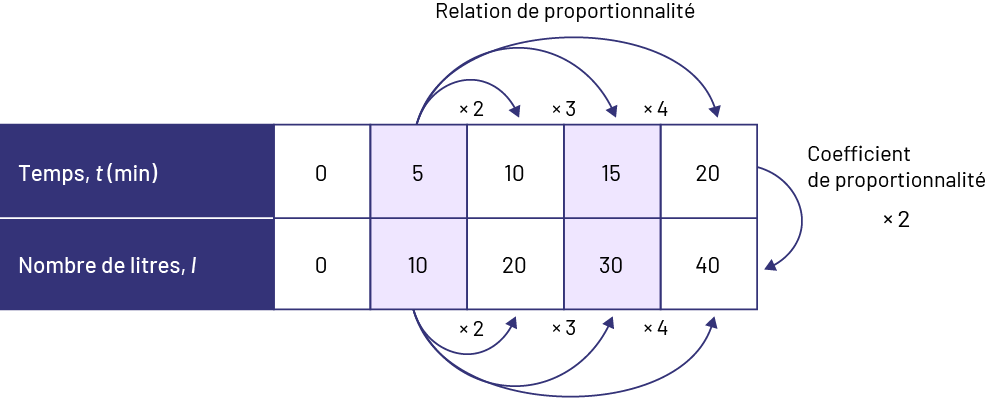Image
Le tableau s’intitule Relation de proportionnalité. Chaque thème possède cinq cases contenant toutes un
chiffre ou un nombre. Le thème Temps en minutes présente les chiffres et nombres zéro, cinq, dix, quinze, vingt. Une
flèche relie cinq à dix en indiquant fois deux. Une flèche relie cinq à quinze en indiquant fois trois. Et une
flèche relie cinq à vingt en indiquant fois quatre. Le thème Nombre de litres présente les chiffres zéro, dix,
vingt, trente, quarante. Une flèche relie dix à vingt en indiquant fois deux. Une flèche relie dix à trente en
indiquant fois trois. Et une flèche relie dix à quarante en indiquant fois quatre. Enfin, une flèche relie le premier
thème au deuxième en indiquant Coefficient de proportionnalité fois deux.
Représentation graphique
Nombre de litres en fonction du temps
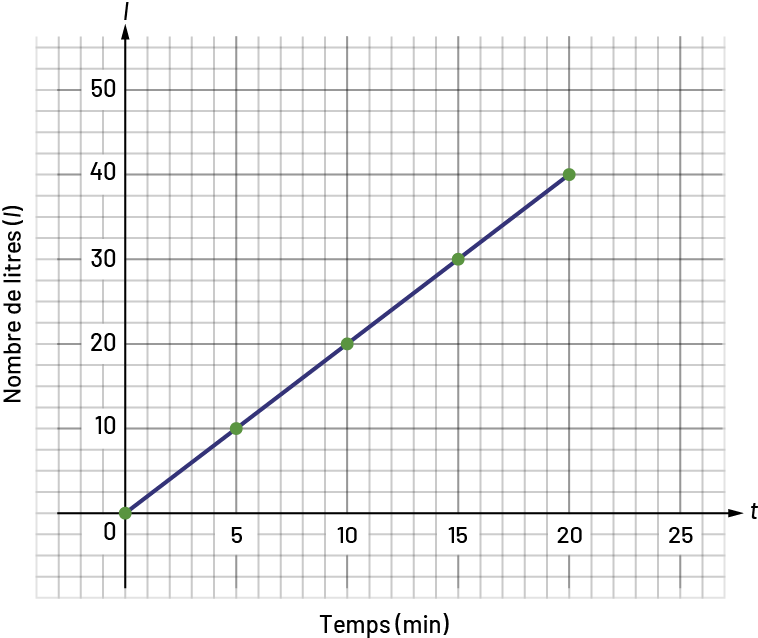Image
Le diagramme présente le temps en minutes sur l’axe horizontal
et le nombre de litres sur l’axe vertical. Partant de zéro, la ligne diagonale traverse les coordonnées cinq virgule
dix, dix virgule vingt, 15 virgule 30, et vingt virgule 40.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 51.
Dans cette situation, la droite débute à (0,0) et l’élève peut voir sur le graphique que si le temps double, le nombre de litres double également.
Les situations comportant une relation de proportionnalité peuvent être résolues intuitivement avec un raisonnement proportionnel.
C’est à partir du cycle moyen que les termes rapport et proportion, ainsi que les notations qui s’y rattachent, sont présentés aux élèves. Lorsqu’il y a une égalité entre deux rapports, il s’agit d’une proportion; par exemple : 2 : 3 = 10 : 15 ou \(\frac{2}{3}\; = \;\frac{{10}}{{15}}\).
Au cycle primaire, les élèves utilisent intuitivement le raisonnement proportionnel pour résoudre des problèmes comprenant deux quantités qui sont dans un rapport de un à plusieurs (par exemple, un gâteau pour huit enfants), de plusieurs à un (par exemple, trois personnes par table) ou de plusieurs à plusieurs (par exemple, deux litres de jus pour cinq personnes).
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 49.
Une relation est non proportionnelle lorsque deux variables ne changent pas au même taux. Par exemple, un dépôt de 5 $ un mois et de 2 $ le mois suivant n’est pas proportionnel, car la croissance n’est pas constante. Sa représentation graphique serait irrégulière, pas une droite.
Cependant, certaines droites sont considérées comme des relations non proportionnelles.
Exemple
Une plombière facture à un client un appel de service ainsi les heures nécessaires afin de réparer un problème. Elle facture donc 40 $ pour l’appel de service et 30 $/heure par la suite. La table de valeurs et le graphique ci-bas représentent cette situation.
| Nombre d’heures | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Montant de la facture, ($) | 40 | 70 | 100 | 130 | 160 | 190 |
Le montant de la facture en fonction du nombre d’heures travaillées
Image
Le diagramme présente le nombre d’heures travaillées sur l’axe horizontal et le montant de la facture en dollars sur
l’axe vertical. La ligne diagonale passe notamment aux coordonnées zéro virgule 40, deux virgule cent, et quatre
virgule 165.
Dans cette situation, la droite débute à (0, 40) et l’élève ne peut pas appliquer le raisonnement proportionnel. L’élève abordera cette notion dans C1.1.
En dehors du cours de mathématiques, le raisonnement proportionnel s’applique dans des matières comme les sciences, la musique et la géographie, ainsi que dans des activités de tous les jours. Les gens se servent du raisonnement proportionnel pour faire des calculs dans le cadre de leurs achats, leurs déclarations d’impôt ou de leurs placements, pour tracer des plans et des cartes, pour prendre des mesures ou faire la conversion de devises étrangères, pour suivre des recettes et les adapter à leurs besoins, ou encore pour déterminer différentes concentrations pour des mélanges et des solutions.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année. 2020. Ministère de l’Éducation de l’Ontario.
Exemple d’un problème dans lequel le raisonnement proportionnel est utilisé au cycle moyen
Dans la recette de gâteau, il y a \(\frac{2}{3}\) de tasse de sucre et 2 tasses de farine. Quelle quantité de farine Mme Larose doit-elle ajouter au mélange si elle y a incorporé \(3\frac{1}{3}\) tasses de sucre? Représenter les quantités qui varient à l’aide d’un diagramme aide les élèves à analyser les relations de proportionnalité.
Image Horizontalement, le mot farine est suivi de cinq flèches
courbées vers le haut possédant chacune un chiffre
au-dessus.Sous le mot farine, il y a le mot sucre, qui est suivi de dix flèches courbées vers le bas; il y a une
fraction
sous chaque duo de flèches.Les deux rangées de flèches sont placées l’une vis-à-vis l’autre.Sous le chiffre deux de la
farine, il y a deux tiers pour le sucre; sous le chiffre quatre de la farine, il y a
quatre tiers pour le sucre, sous le chiffre six il y a six tiers, sous le chiffre huit il y a huit tiers et sous le
nombre dix, il y a dix tiers.
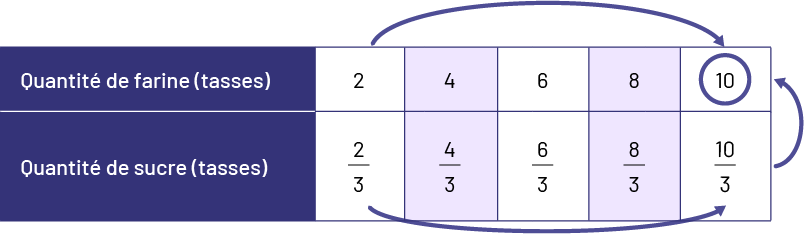
Ce type de représentation montre que la quantité d’ingrédients de la recette est quintuplée si \(3\frac{1}{3}\) tasses de sucre sont utilisées. Transposée dans un tableau, la représentation s’apparente à une représentation familière pour les élèves, soit la table de valeurs, qui a l’avantage de les aider à vérifier la présence d’une relation multiplicative entre les quantités.
Image
Le tableau présente deux thèmes : Quantité de farines en tasses, qui présente cinq cases possédant chacune un chiffre,
et Quantité de sucre en tasses, qui présente cinq cases possédant chacune une fraction. Les chiffres pour la farine
vont comme suit : deux, quatre, six, huit, dix. Dix est encerclé, et une flèche relie deux à dix. Les fractions pour
le sucre vont comme suit : deux tiers, quatre tiers, six tiers, huit tiers, dix tiers. Une flèche relie deux tiers à
dix tiers; et une flèche relie dix tiers au nombre dix de la farine.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 50.
Exemple d’un problème avec des variables
Martine travaille à temps partiel dans un parc aquatique. Son taux horaire est de 15,25 $/heure. Comment peut-elle calculer son salaire?
Stratégie A
Elle peut utiliser une équation avec des variables.
\(s\; = \;15,25\;\$ \; \times \;h\)
La variable s représente le salaire gagné et la variable h représente le nombre d’heures travaillées.
Puisque pour chaque heure de travail elle gagne 15,25 $, alors pour trouver son salaire, il suffit de multiplier 15,25 $ par le nombre d’heures travaillées.
Stratégie B
Elle peut utiliser des rapports équivalents.
\(\frac{{15,25\;\$ }}{{1\;{\rm{heure}}}}\; = \;\frac{s}{h}\)
Cette situation est proportionnelle, donc on compare deux rapports équivalents. Le premier est le taux horaire 15,25 $/heure et le second est le salaire gagné en fonction du nombre d’heures travaillées (s/h). La division du premier rapport sera égale à la division du second rapport.
- Martine a travaillé 12 heures cette semaine, quel est son salaire?
Pour résoudre le problème avec les 2 stratégies énumérées ci-haut, je remplace la variable h par 12.
Stratégie A
\(\begin{align}s\; &= \;15,25\;\$ \; \times \;h\\ &= \;15,25\;\$ \; \times \;12\\ &= \;15,25\;\$ \; \times \;\left( {10\; + \;2} \right)\\ &= \;\left( {15,25\;\$ \; \times \;10} \right)\; + \;\left( {15,25\;\$ \; \times \;2} \right)\\ &= \;152,50\;\$ \; + \;30,50\\ &= \;183\;\$ \end{align}\)
Stratégie B
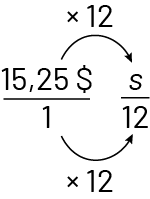
Image Quinze et 25 dollars sur une heure égale « S » sur douze. Quinze et 25 dollars fois douze sur
une fois douze égale 183 dollars sur douze. « S » égale quinze et 25 dollars fois douze, égale quinze et 25 dollars
fois parenthèse ouvrante dix plus deux parenthèse fermante, égale parenthèse ouvrante quinze et 25 fois dix
parenthèse fermante plus parenthèse ouvrante quinze et 25 fois deux parenthèse fermante, égale 152 et 50 plus 30 et
50, égale 183 dollars. Martine gagne 183 $ pour 12 heures de travail.
Connaissance : raisonnement proportionnel
L’élève utilise le raisonnement proportionnel dès le début de l’apprentissage des mathématiques, par exemple, en voyant que 8 équivaut à \(2 \times 4\) ou \(4 \times 2\) et pas seulement à « 1 de plus que 7 ». Le raisonnement proportionnel est utilisé à des stades ultérieurs de l’apprentissage lorsque l’élève comprend qu’une vitesse de 50 km/h est l’équivalent d’une distance de 25 km parcourue en 30 minutes.
L’élève continue d’employer le raisonnement proportionnel en étudiant la pente d’une courbe ou les dérivées. Le raisonnement proportionnel consiste, à la base, dans la visualisation des nombres selon leur valeur relative plutôt que leur valeur absolue. L’élève applique un raisonnement proportionnel pour établir qu’un groupe qui passe de 3 à 9 enfants subit une augmentation plus importante qu’un autre qui passe de 100 à 150 enfants puisque, dans le premier cas, le nombre a triplé alors que, dans le deuxième cas, il n’a augmenté que de 50 % et n’a même pas doublé.
Les activités des années des cycles primaire et moyen contribuent au développement du raisonnement proportionnel. Par exemple, en comparant la valeur d’un ensemble de quatre pièces de cinq cents à la valeur d’un ensemble de quatre pièces d’un cent, l’élève développe son raisonnement proportionnel.
Aux cycles moyen et intermédiaire, l’élève travaille directement avec les fractions et leur utilisation dans le contexte des rapports, des taux et des pourcentages.
Dans le raisonnement proportionnel, on s’attarde aux relations et on compare des quantités ou des valeurs. Comme a dit Van de Walle, « Il est malaisé de définir le raisonnement proportionnel. Il ne s’agit pas d’un type de raisonnement qu’on est capable de tenir ou non : il s’acquiert progressivement au fil du temps. On peut le décrire notamment comme la capacité à réfléchir à des relations multiplicatives entre des quantités et à comparer de telles relations, représentées symboliquement sous forme de rapports. » (2008, p. 163) On a parfois tendance à croire que le raisonnement proportionnel se limite à l’étude des rapports, des taux et des nombres rationnels comme les fractions, les décimales et les pourcentages alors, qu’en fait, il touche toutes les sphères des mathématiques. Par exemple, la proportionnalité est un aspect important des mesures, y compris de la conversion des unités et des relations de multiplication des dimensions qui existent entre l’aire et le volume.
Exemple de raisonnement proportionnel en mesure
Quelle figure contient le plus de couleur?
Image Deux rectangles sont placés l’un sous l’autre. Le rectangle « A » est plus long que le rectangle « B ».
Il est divisé en deux parties égales, la première est violette et l’autre est blanLa première partie du
rectangle « B » est violette et de la même longueur que celle du rectangle « A ». Sa
deuxième partie, blanche, est plus courte et fait environ la moitié de celle du rectangle « A ».
Donner à l’élève des représentations non numériques l’oblige à appliquer un raisonnement qualitatif. On peut alors stimuler des discussions enrichissantes sur la proportionnalité. Vous trouverez d’autres exemples de ce type dans Small (2008),Van de Walle (2008) et dans Continuum and Connections: Big Ideas and Proportional Reasoning K–12.
Source : Qu’est-ce que le raisonnement proportionnel?, p. 3.
Connaissance : rapport
Relation entre deux grandeurs exprimées sous la forme du quotient des nombres qui les caractérisent.
Par exemple, dans l’ensemble de 5 billes ci-dessus,
- il y a un rapport de 2 à 3 (\(\frac{2}{3}\) ou 2 : 3) entre le nombre de billes blanches et le nombre de billes noires. (rapport partie : partie)
- il y a un rapport de 2 à 5 (\(\frac{2}{5}\) ou 2 : 5) entre le nombre de billes blanches et le nombre total de billes. Ceci peut être interprété comme \(\frac{2}{5}\) des billes sont blanches. (rapport partie : tout)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 49.
Connaissance : rapports équivalents
Lorsque 2 rapports peuvent augmenter ou diminuer simultanément selon le même facteur.
Exemple
Le rapport 3 : 5 ou est équivalent au rapport 6 : 10 ou en multipliant les termes par le même facteur de 2.
Note : Des rapports équivalents se déterminent de la même façon que des fractions équivalentes, c’est-à-dire en multipliant ou en divisant chaque terme (ou partie) du rapport par le même facteur ou diviseur. Si la valeur d’un terme (ou partie) d’un rapport est modifiée, il y aura un effet direct sur celui-ci.
Source : En avant, les maths! 5e année, CM, Nombres, p. 2.
Connaissance : coefficient de proportionnalité
2 grandeurs sont proportionnelles si la valeur de l’une s’obtient en multipliant ou en divisant la valeur de l’autre par un même nombre.
Un tableau présente deux thèmes : Nombre d’élèves et Nombre de
souliers. Ils ont chacun quatre cases contenant un nombre. Les nombres d’élèves vont comme suit : quatre, six, neuf,
quinze. Les nombres de souliers vont comme suit : huit, 12, 18, 30. Une flèche relie le premier thème au deuxième en
indiquant fois deux.
Source : En avant, les maths! 5e année, CM, Nombres, p. 2.
Connaissance : tableau de rapports
Modèle pouvant être utilisé pour développer une compréhension de la multiplication, des fractions équivalentes, de la division et du raisonnement proportionnel.
| Sacs de farine | 1 | 3 | 4 | 6 | ? |
| Eau | 3 | 9 | ? | ? | 6 |
Source : En avant, les maths! 5e année, CM, Nombres, p. 2.
Connaissance : taux
Un taux décrit la relation entre 2 quantités exprimées avec des unités différentes (par exemple, des objets avec des dollars ou des kilomètres avec des heures).
Source : En avant, les maths! 5e année, CM, Nombres, p. 2.
Connaissance : pourcentage
Le pourcentage est une façon particulière de présenter une fraction. Il est souvent employé dans la vie courante. Une expression numérique comme 30 % (qui se lit « trente pour cent ») est en réalité une autre notation du nombre trente centièmes, soit \(\frac{30}{100}\) ou 0,30. Afin de faciliter la compréhension du concept de pourcentage, il faut d’abord amener les élèves à établir le lien entre le pourcentage et la fraction dont le dénominateur est 100, et ce, à l’aide de matériel concret ou semi-concret. Le pourcentage représente également un rapport de 1 :100.
Exemple
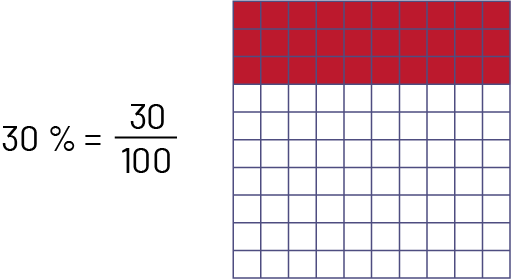
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.