B2.8 Compare proportional situations and determine unknown values in proportional situations, and apply proportional reasoning to solve problems in various contexts.
Skill: Identifying Proportional and Non-Proportional Situations and Applying Proportional Reasoning
The ability to master proportional reasoning is a critical factor in the understanding and application of mathematics. Lamon estimates that more than 90 percent of students entering high school lack the reasoning skills necessary to fully understand mathematics and science, and are ill-prepared for real-world applications in statistics, biology, geography or physics (Lamon, 2005, p. 10). A student may be able to solve a problem based on proportions using a method that has been memorized, but this does not mean that they can apply proportional reasoning in the course of solving the problem.
Source: Paying Attention to Proportional Reasoning, 2012, Ontario Ministry of Education, p. 4.
Multiplicative Reasoning
Multiplicative reasoning is a concept that requires the ability to deal with several ideas or quantities at once. The idea is to see problems in relative rather than absolute values. Consider the following problem, "If one dog's weight goes from 5 kg to 8 kg and another dog's weight goes from 3 kg to 6 kg, which dog gained more weight?" If the student is approaching the problem from the perspective of absolute values or addition, they may be inclined to answer that the two dogs have gained equal weight. However, based on relative values, the student may argue that the second dog gained more weight since it doubled its starting weight as opposed to the first dog, which would have had to reach 10 kg for its relative weight gain to be equivalent. The following table visually illustrates the two answers to this problem. If it is true that the two answers can be defended, it is on the relative value (multiplicative reasoning) that proportional reasoning is based.
| Here is student thinking that is absolute: | Here is student thinking that is relative: |
|---|---|
| The first dog grew by 3 kg. The second dog grew by 3 kg. They grew the same amount.
Dog 1:
Dog 2:  |
The second dog grew more since he doubled his previous weight, unlike the first dog who would have needed to be 10 kg to grow by the same relative amount.
Dog 1: 
Less than doubled weight Dog 2: 
Doubled weight |
Why is this important?
Helping students bridge from additive to multiplicative thinking is complex but starts early. It forms the backbone of the Mathematics Curriculum and includes important and interconnected ideas such as multiplication, division, fractions, decimals, ratios, percentages and linear functions. It requires time, a variety of situations and opportunities to construct their understanding in multiple ways.
Source: Paying Attention to Proportional Reasoning, 2012, Ontario Ministry of Education. p. 5-6.
Proportional Relationships
There is a proportional relationship between two quantities when these quantities can increase or decrease simultaneously by the same factor. For example, if one of the two quantities is tripled, the other is also tripled. The ratio between the two quantities is then constant (for example, \(\frac{1}{6}\; = \;\frac{3}{{18}}\)). Such equality between two ratios is called a proportion.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 39.
Example 1
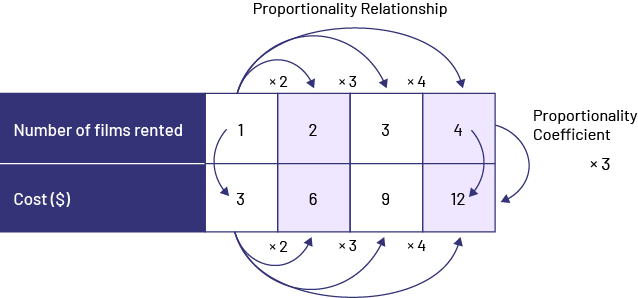
Example 2
An aquarium, empty at the beginning, fills at a rate of 2 litres of water per minute. Represent, in several ways, the number of litres of water in the aquarium according to time, in minutes.
Visual Representation (Ratio Table)

Graphical Representation
Number of Litres According to Time
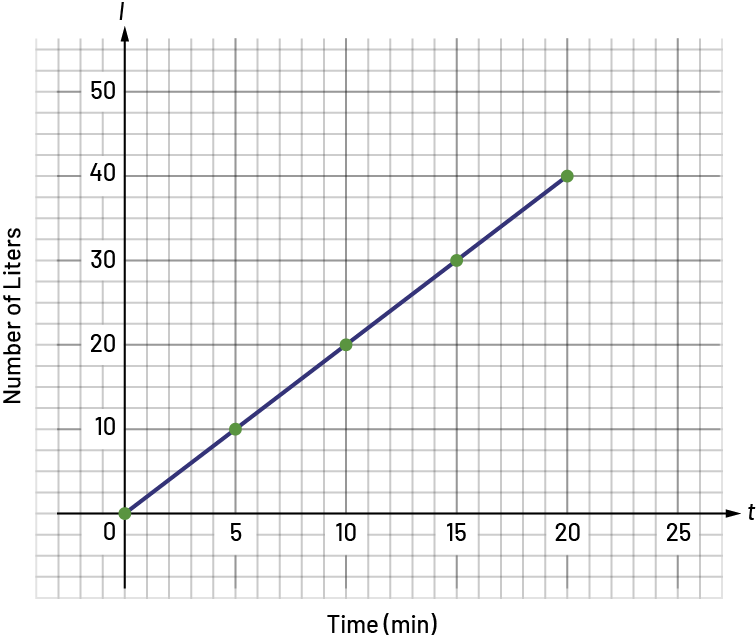
Source: translated from Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 51.
In this situation, the line starts at (0,0) and the student can see from the graph that if the time doubles, the number of litres also doubles.
Situations involving a proportional relationship can be solved intuitively with proportional reasoning.
From the Junior Division onwards, students are introduced to the terms ratio and proportion, and the notations associated with them. When two ratios are equal, it is a proportion; for example: 2:3 = 10:15 or \(\frac{2}{3}\; = \;\frac{{10}}{{15}}\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 49.
A relationship is non-proportional when two variables do not change at the same rate. For example, a deposit of $5 one month and $2 the next is not proportional because the growth is not constant. Its graphical representation would be irregular, not a straight line.
However, some straight lines are considered to be non-proportional relationships.
Example
A plumber charges a customer for a service call and the hours required to repair a problem. She therefore charges $40 for the service call and $30/hour afterwards. The table of values and the graph below represent this situation.
| Number of Hours | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Invoice Amount ($) | 40 | 70 | 100 | 130 | 160 | 190 |
Invoice Amount According to Hours Worked

In this situation, the line starts at (0, 40) and the student cannot apply proportional reasoning. This concept is addressed in C1.1.
Beyond the mathematics classroom, proportional reasoning is evident in other subject areas like science, music and geography, as well as in everyday activities. People use proportional reasoning to calculate best buys, taxes and investments, to work with drawings and maps, to perform measurement or monetary currency conversions, to adjust recipes or to create various concentrations of mixtures and solutions.
Source: Paying Attention to Proportional Reasoning, 2012, Ontario Ministry of Education. p. 4.
Example of a Problem With Variables
Martine works part-time at a water park. Her hourly rate is $15.25/hour. How can she calculate her salary?
Strategy A
She can use an equation with variables.
\(s\; = \;\$15.25\; \; \times \;h\)
The variable s represents the salary earned and the variable h represents the number of hours worked.
Since for every hour she works she earns $15.25, then to find her salary, simply multiply $15.25 by the number of hours worked.
Strategy B
She can use equivalent ratios.
\(\frac{{\$15.25\; }}{{1\;{\rm{time}}}}\; = \;\frac{s}{h}\)
This is a proportional relationship, so we are comparing two equivalent ratios. The first is the hourly rate $15.25/hour and the second is the salary earned based on the number of hours worked(s/h). The division of the first ratio will equal the division of the second ratio.
- Martine worked 12 hours this week, what is her salary?
To solve the problem with the two strategies listed above, replace the variable h by 12.
Strategy A
\(\begin{align}s\; &= \;\$15.25\; \; \times \;h\\ &= \;\$15.25\; \; \times \;12\\ &= \;\$15.25\; \; \times \;\left( {10\; + \;2} \right)\\ &= \;\left( {\$15.25\; \ ; \times \;10} \right)\; + \;\left( {\$15.25\; \; \times \;2} \right)\\ &= \;\$152.50\; \; + \;30.50\\ &= \;\$183\; \end{align}\)
Strategy B
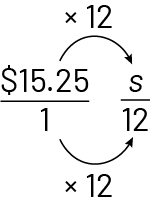

Martine earns $183 for 12 hours of work.
Knowledge: Proportional Reasoning
Students use proportional reasoning in early math learning, for example, when they think of 8 as two fours or four twos rather than thinking of it as one more than seven. They use proportional reasoning later in learning when they think of how a speed of 50 km/h is the same as a speed of 25 km/30 min.
Students continue to use proportional reasoning when they think about slopes of lines and rates of change. The essence of proportional reasoning is the consideration of numbers in relative terms, rather than absolute terms. Students are using proportional reasoning when they decide that a group of 3 children growing to 9 children is a more significant change than a group of 100 children growing to 150, since the number tripled in the first case; but only grew by 50%, not even doubling, in the second case.
Activities in the primary grades support the development of proportional reasoning. For example, if we ask students to compare the worth of a group of four nickels to the worth of a group of four pennies, we are helping them to develop proportional reasoning.
In the Junior and Intermediate grades, students work directly with fractional equivalence, ratio, rate and percent.
Proportional reasoning involves thinking about relationships and making comparisons of quantities or values. In the words of John Van de Walle, “Proportional reasoning is difficult to define. It is not something that you either can or cannot do but is developed over time through reasoning … It is the ability to think about and compare multiplicative relationships between quantities” (2006, p. 154). Proportional reasoning is sometimes perceived as only being the study of ratios, rates and rational numbers including work with fractions, decimals and percents, but it actually permeates all strands of mathematics. For example, proportionality is an important aspect of measurement, including unit conversions and understanding the multiplicative relationships of dimensions in area and volume.
An example of proportional reasoning in area measurement.
Which shape is more purple?

Giving students non-numerical representations which require qualitative reasoning can evoke rich discussions about proportionality.
Source: Paying Attention to Proportional Reasoning, 2012, Ontario Ministry of Education, p. 3.
Knowledge: Ratios
Relationship between two quantities expressed as the quotient of the numbers that characterize them.

For example, in the set of 5 marbles above,
- there is a ratio of 2 to 3 ( \(\frac{2}{3}\) or 2:3) between the number of white marbles and the number of blue marbles. (part: part ratio)
- there is a ratio of 2 to 5 (\(\frac{2}{5}\) or 2:5) between the number of white marbles and the total number of marbles. This can be interpreted as \(\frac{2}{5}\) marbles are white. (part:whole ratio)
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 49.
Knowledge: Equivalent Ratios
When two ratios can be increased or decreased simultaneously by the same factor.
Example
The ratio 3:5 is equivalent to the ratio 6:10, and is obtained by multiplying both terms of the first ratio by the same factor of 2.
Note: Equivalent ratios are determined in the same way as equivalent fractions, that is, by multiplying or dividing each term (or part) of the ratio by the same factor.
Source: translated from En avant, les maths! 5e , CM, Nombres, p. 2.
Knowledge: Scale Factor
Two quantities are proportional if the value of one is obtained by multiplying or dividing the value of the other by the same number, which is the scale factor.

Source: translated from En avant, les maths! 5e , CM, Nombres, p. 2.
Knowledge: Ratio Table
Model that can be used to develop an understanding of multiplication, equivalent fractions, division, and proportional reasoning.
| Flour bags | 1 | 3 | 4 | 6 | ? |
| Water | 3 | 9 | ? | ? | 6 |
Source: translated from En avant, les maths! 5e , CM, Nombres, p. 2.
Knowledge: Rate
A rate describes the relationship between two quantities expressed with different units (for example, objects with dollars or kilometres with hours).
Source: translated from En avant, les maths! 5e , CM, Nombres, p. 2.
Knowledge: Percent
A percent is a special kind of fraction. It is often used in everyday life. A numeric expression such as 30% (which reads "thirty percent") is actually another notation for the number thirty hundredths, that is \(\frac{30}{100}\) or 0.30. To facilitate understanding of the concept of percent, students must first be introduced to the relationship between the percent and the fraction with a denominator of 100, using concrete or visual (semi-concrete) materials. The percentage also represents a ratio of 1:100.
Example

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 34