E1.3 Construire et décrire des figures planes et des solides qui sont symétriques.
HABILETÉ : CONSTRUIRE UNE FIGURE PLANE OU UN SOLIDE SYMÉTRIQUE
L’élève construit des figures planes ou des solides symétriques en utilisant les stratégies suivantes.
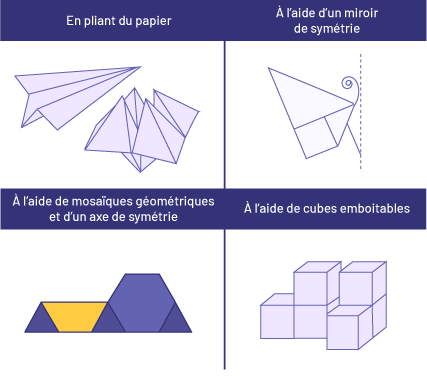
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
HABILETÉ : DÉCRIRE LA SYMÉTRIE
Réflexion
La réflexion fait partie de la vie quotidienne de l’enfant. Elle ou il se regarde dans le miroir, se voit et réagit à sa réflexion. Elle ou il observe le reflet des montagnes dans le lac, le reflet de son corps dans une vitrine, etc.
En 1re année, on présente le concept de symétrie. L’élève repère des figures symétriques dans son environnement, les reproduit à l’aide de pliage, de découpage ou du Mira.
Exemple 1
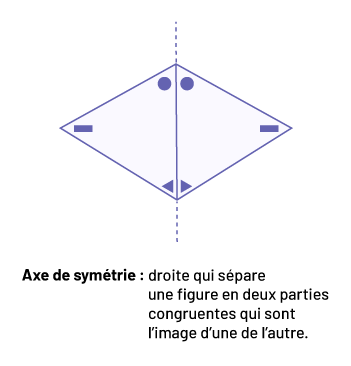
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 61.
CONNAISSANCE : CONGRUENCE
Congruentes : se dit de deux figures planes dont les mesures de tous les éléments correspondants (côtés et angles) sont égales.
La congruence est une relation particulière entre des figures planes dont les mesures de tous les éléments correspondants (côtés et angles) sont égales. Bien que les élèves ne démontrent cette relation qu’au cycle moyen, il importe que le personnel enseignant du cycle primaire le comprenne afin que les élèves en 2e et en 3e année puissent explorer et construire le concept des « figures planes régulières » – une figure dont les côtés et les angles sont tous congrus. À ce moment, les élèves découvrent que celles-ci « se ressemblent en tous points » en les superposant les unes sur les autres pour voir à quel point elles correspondent.
Cependant, les élèves du cycle primaire rencontreront souvent des concepts liés à la congruence en géométrie, notamment :
- les faces d’un solide peuvent être congruentes (par exemple, les faces d’un cube sont des carrés congruents; les deux bases d’un prisme à base pentagonale sont en forme de pentagones congruents);
- les translations (déplacer une forme) et les réflexions (faire refléter une forme comme dans un miroir) donnent une image congruente à la figure initiale.
Le concept de congruence s’applique aussi avec les solides.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 18.
