E1.3 Construct and describe two-dimensional shapes and three-dimensional objects that have matching halves.
Skill: Constructing a Two-Dimensional Shape or a Symmetrical Three-Dimensional Object
Students will construct two-dimensional shapes or symmetrical three-dimensional objects using the following strategies.
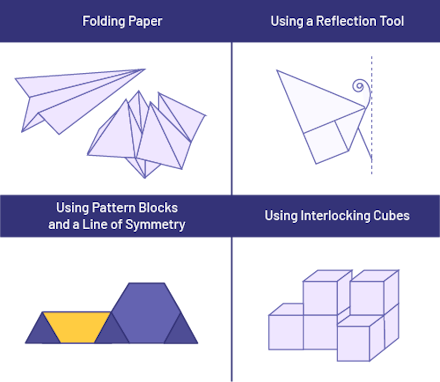image 2 column and 2 rows table. The first column, first row: « By folding paper. » The second column, first row: « With the help of a symmetry mirror. » The first column, second row: « With the help of geometric mosaics and a line of symmetry. » The second column, second row: « With the help of connecting cubes. »
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Skill: Describing Symmetry
Reflection
Reflection is part of a child's daily life. For example, they look in a mirror, see themselves and react to their reflection. They observe the reflection of the mountains in the lake, the reflection of their body in a window, etc.
In Grade 1, the concept of symmetry is introduced, and students locate symmetrical shapes in their environment and reproduce them using folding, cutting, or a Mira.
Example 1
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 61.
Knowledge: Congruence
Congruent describes two two-dimensional shapes whose measures of all corresponding elements (sides and angles) are equal.
Congruence is a special relationship between two-dimensional shapes whose measures of all corresponding elements (sides and angles) are equal. Although students only demonstrate this relationship in the junior grades, it is important for teachers in the primary grades to understand this so that students in grades 2 and 3 can explore and construct the concept of "regular two-dimensional shapes" - a figure whose sides and angles are all congruent. At this point, students discover that these "look alike in every way" by superimposing them on top of each other to see how well they match.
However, elementary students will often encounter concepts related to congruence in geometry, including:
- the faces of a three-dimensional object can be congruent (for example, the faces of a cube are congruent squares; the two bases of a pentagon-based prism are congruent pentagons);
- translations (moving a shape) and reflections (reflecting a shape as in a mirror) give an image congruent to the initial shape.
The concept of congruence also applies to three-dimensional objects.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 18.