GEEM - Enseignement et apprentissage

E1.1 Classer et identifier des figures planes en comparant le nombre de côtés, la longueur des côtés, les angles et le nombre d’axes de symétrie.

ACTIVITÉ 1 : UNE FIGURE PARMI TANT D’AUTRES

L’élève se représente mentalement les figures planes sous diverses formes et orientations ou positions. En reconnaissant qu’une figure plane est composée de côtés, de côtés congrus et de sommets, l’élève peut classer les figures planes en fonction des propriétés des grandes familles de polygones. Ainsi naîtra le besoin de nommer un ensemble de polygones qui répond à certaines propriétés très précises.

Pour réaliser l’activité, l’élève doit pouvoir :

reconnaître le triangle, le carré, le rectangle, le quadrilatère, le pentagone, l’hexagone, l’heptagone et l’octogone;
classer les figures selon un certain nombre d’attributs;
comparer les propriétés des figures planes (par exemple, nombre de côtés, nombre de sommets, nombre de côtés congrus);
déterminer si deux figures sont congruentes, en mesurant ou en superposant les figures pour savoir si les côtés sont congrus;
tracer des lignes droites verticales, horizontales et obliques.

Dans cette activité, l’élève construit de nouvelles figures d’après d’autres figures. L’élève classe les nouvelles figures créées selon le nombre de côtés.

L’activité a pour but de permettre à l’élève de comparer les propriétés des grandes familles de polygones;

L’activité fait également appel à d’autres concepts mathématiques liés aux domaines :

Données, puisque l’élève trie et classe des objets qui sont des figures planes;
Sens de l’espace, puisque l’élève s’initie graduellement au concept d’aire en superposant des figures.

Vocabulaire mathématique

figure plane, triangle, carré, rectangle, quadrilatère, pentagone, hexagone, heptagone, octogone, figure congruente, côté congru, paire de côtés congrus

Matériel

ensembles de mosaïques géométriques
feuilles de 28 cm × 43 cm
crayons

Avant l’apprentissage (mise en train)

Former des équipes de deux élèves. Remettre à chaque équipe un ensemble de mosaïques géométriques.

Demander aux élèves :

de placer sur leur table les six différentes figures de l’ensemble;
de les nommer (l’hexagone jaune, le carré orange, le triangle vert, le quadrilatère rouge, le quadrilatère beige et le quadrilatère bleu);
de regrouper les figures planes par famille selon le nombre de côtés (les quadrilatères, le triangle et l’hexagone);
de nommer d’autres familles de figures planes selon le nombre de côtés (les pentagones, les heptagones et les octogones).

Pendant l’apprentissage (exploration)

Expliquer aux élèves qu’elles et ils vont créer de nouvelles formes géométriques en assemblant des mosaïques géométriques.

Leur demander d’en créer le plus possible.

Donner les directives suivantes :

utiliser les mosaïques géométriques pour construire de nouvelles formes géométriques;
tracer le contour des nouvelles formes afin d’obtenir une nouvelle figure plane;
écrire le nom de la nouvelle figure plane en dénombrant le nombre de côtés.

Allouer aux élèves le temps nécessaire pour leur permettre de réaliser le travail.

Circuler parmi les élèves et intervenir au besoin en posant des questions telles que :

Avec quelles mosaïques géométriques as-tu construit cette figure?
Combien de côtés cette nouvelle figure a-t-elle?
Combien de sommets cette figure a-t-elle?
Comment se nomme cette nouvelle figure?
Comment peux-tu vérifier si cette figure est congruente à une autre figure sur ta feuille?
Si tu tournes la figure de côté, est-elle congruente à une autre figure sur ta feuille?
Observe tous les triangles que tu as créés. Qu’ont-ils de semblable? de différent?
Observe tous les pentagones que tu as créés. Ont-ils toujours cinq côtés? Ont-ils parfois cinq côtés congrus?
Observe tous les rectangles que tu as créés. Ont-ils toujours deux paires de côtés congrus?
Qu’est-ce que le carré et le rectangle ont en commun?

Après l’apprentissage (objectivation/transfert des connaissances)

Afficher toutes les nouvelles figures.

Demander aux élèves de présenter leurs nouvelles figures et d’en décrire la construction.

Exemples

On a utilisé quatre petits carrés orange pour former un grand carré.
On a utilisé deux triangles verts pour former un quadrilatère.
On a utilisé un triangle et un carré pour former un pentagone.

Classer, en groupe-classe, les nouvelles figures en familles de triangles, de quadrilatères, etc.

Poser des questions telles que :

Qu’est-ce que les triangles ont de semblable?
Qu’est-ce que les triangles ont de différent?
Qu’est-ce que les quadrilatères ont de semblable?
Qu’est-ce que les quadrilatères ont de différent?
Qu’est-ce que les pentagones ont de semblable?
Qu’est-ce que les pentagones ont de différent?
Qu’est-ce que les hexagones ont de semblable?
Qu’est-ce que les hexagones ont de différent?
Qu’est-ce que les heptagones ont de semblable?
Qu’est-ce que les heptagones ont de différent?
Qu’est-ce que les octogones ont de semblable?
Qu’est-ce que les octogones ont de différent?

Exemples de critères d’évaluation

L’élève :

construit des formes géométriques;
trace le contour des formes géométriques construites;
nomme les figures planes correspondantes aux contours;
détermine si deux figures planes sont congruentes en les superposant;
indique les côtés congrus d’une figure;
classe les figures selon le nombre de côtés;
décrit des figures selon leurs propriétés;
reconnaît que toutes les figures planes d’une même famille ont le même nombre de côtés et de sommets;
reconnaît que la forme, les dimensions et la position peuvent changer d’une figure à l’autre.

Différenciation pédagogique

L’activité peut être modifiée pour répondre aux besoins des élèves.

Pour faciliter la tâche	Pour enrichir la tâche
demander aux élèves de former une figure de chaque famille plutôt que plusieurs; dire aux élèves de trouver les nouvelles figures en utilisant des figures identiques seulement (par exemple, deux triangles pour former un quadrilatère; quatre carrés pour former un carré; trois carrés pour former un rectangle).	Reprendre le même genre d’activité en utilisant des pièces d’un tangram.

Suivi à la maison

À la maison, l’élève peut repérer et décrire des objets composés de formes géométriques (par exemple, la fenêtre est un grand rectangle formé de deux petits rectangles).

Source : Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, p. 147-151.

ACTIVITÉ 2 : DES AXES DE SYMÉTRIE

Distribuer aux élèves une copie de l’annexe 3PF.5, deux copies de l’annexe 3PF.6, un géoplan (5 × 5), des élastiques de couleur différente et un Mira.

Donner les directives suivantes :

construire chaque figure sur un géoplan;
trouver, à l’aide du Mira, les axes de symétrie de chaque figure;
utiliser des élastiques de couleur différente pour représenter chaque axe de symétrie d’une même figure;
reproduire chaque figure sur le papier à points;
tracer d’une couleur différente chaque axe de symétrie dans une même figure;
remplir le tableau intitulé Les axes de symétrie.

Faire la mise en commun en posant des questions telles que :

Un triangle a-t-il toujours trois axes de symétrie?
Un rectangle a-t-il quelquefois aucun (zéro) axe de symétrie?
Un hexagone a-t-il quelquefois quatre axes de symétrie?
Un carré a-t-il toujours quatre axes de symétrie?

Note : Il est impossible de construire un pentagone régulier, un hexagone régulier ou un octogone régulier sur un géoplan, puisque la distance entre deux points à la diagonale est plus grande que la distance entre deux points à la verticale ou à l’horizontale.

Source : Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, p. 162.

ACTIVITÉ 3 : DES QUADRILATÈRES SYMÉTRIQUES

Distribuer aux élèves une copie de l’annexe 3PF.6, un géoplan, des élastiques et un Mira.

Présenter les problèmes suivants.

Construis un quadrilatère qui a un axe de symétrie.
Construis un hexagone qui n’a aucun axe de symétrie.
Construis deux quadrilatères différents qui ont chacun deux axes de symétrie.
Construis un triangle qui a un axe de symétrie.
Construis une figure plane qui a quatre axes de symétrie.

Dans chaque cas, demander :

de construire la figure sur le géoplan;
d’utiliser le Mira pour trouver les axes de symétrie;
de reproduire la figure sur le papier à points;
de tracer chaque axe de symétrie d’une couleur différente à l’intérieur d’une même figure.

Former des équipes de quatre élèves et leur demander de comparer les figures construites à chaque problème.

Exemples de quadrilatères construits au premier problème :

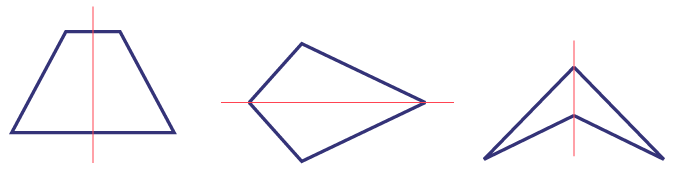
Un trapèze dont l’axe de symétrie vertical est placé en rouge.Un losange dont l’axe de symétrie est placé à l’horizontale, l’axe est en rouge.Un quadrilatère, en forme de pointe de flèche, est traversé par une ligne rouge qui représente l’axe.

Source : Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, p. 162-163.

ACTIVITÉ 4 : DESSINER AVEC SYMÉTRIE

Demander aux élèves de créer un dessin qui contient au moins cinq des figures planes suivantes : triangle, carré, rectangle, autre quadrilatère, pentagone, hexagone, heptagone et octogone.

Exemple

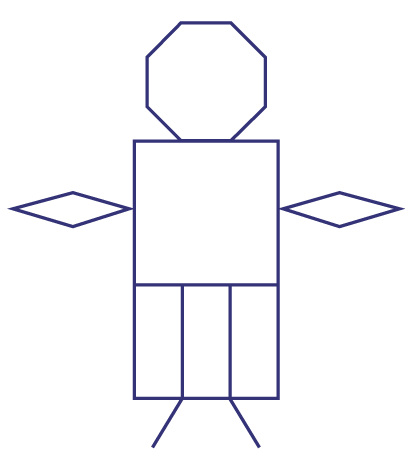
Un personnage est représenté avec des figures, comme suit :La tête est un hexagone. Le corps est un carré. Les bras sont représentés par deux losanges. Les jambes sont des rectangles. Deux droites représentent les pieds.

Dire aux élèves de tracer tous les axes de symétrie de chaque figure plane.

Exemple

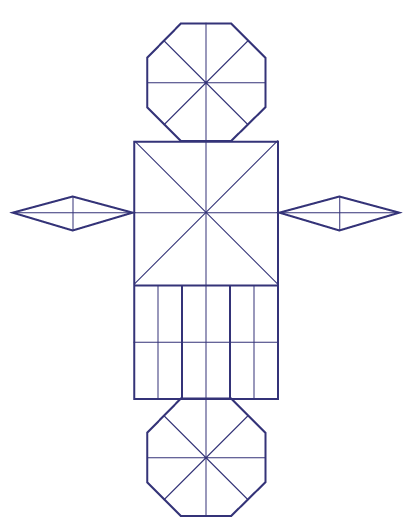
Le personnage formé avec les figures est représenté avec tous les axes de symétrie de toutes les figures planes qui le représentent.

Source : Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, p. 164-165.