GEEM - Teaching and Learning

E1.1 Sort and identify two-dimensional shapes by comparing number of sides, side lengths, angles, and number of lines of symmetry.

Activity 1: One of Many Shapes

The student mentally represents two-dimensional shapes in various shapes and orientations or locations. By recognizing that a two-dimensional shape is composed of sides, congruent sides, and vertices, the student can sort two-dimensional shapes according to the properties of the families of polygons. Thus, the need to name a set of polygons that meet certain very specific properties will arise.

To complete the activity, the student must be able to:

identify the triangle, square, rectangle, quadrilateral, pentagon, hexagon, heptagon, and octagon;
sort the shapes according to a number of attributes;
compare properties of two-dimensional shapes (for example, number of sides, number of vertices, number of congruent sides);
determine if two shapes are congruent by measuring or overlapping the shapes to see if the sides are congruent;
draw vertical, horizontal, and oblique straight lines.

In this activity, the student constructs new shapes based on other shapes. The student ranks the new shapes created according to the number of sides.

In this activity, students compare the properties of the families of polygons;

The activity also draws on other mathematical concepts related to the strands:

Data, since the student sorts objects that are two-dimensional shapes;
Spatial Sense, since the student is gradually introduced to the concept of area by superimposing shapes.

Mathematical Vocabulary

two-dimensional shape, triangle, square, rectangle, quadrilateral, pentagon, hexagon, heptagon, octagon, congruent shape, congruent side, pair of congruent sides

Material

sets of pattern blocks
sheets of 28 cm × 43 cm paper
pencils

Before Learning (Warm-Up)

Form teams of two students and give each team a set of pattern blocks.

Ask students to:

place the six different shapes of the set on their table;
name them (the yellow hexagon, the orange quadrilateral, the green triangle, the red quadrilateral, the beige quadrilateral, and the blue quadrilateral);
group two-dimensional shapes by family according to the number of sides (quadrilaterals, triangle, and hexagon);
name other families of two-dimensional shapes that are not a part of the set according to the number of sides (pentagons, heptagons, and octagons).

Active Learning (Exploration)

Explain to students that they will create new geometric shapes by assembling pattern blocks.

Ask them to create as many unique shapes as possible.

Provide the following instructions:

use pattern blocks to build new geometric shapes;
draw the outline of the new shapes to obtain a new two-dimensional shape;
write the name of the new two-dimensional shape by counting the number of sides.

Allow students the time necessary to complete the assignment.

Circulate among students and provide support as needed by asking questions. For example:

Which pattern blocks did you use to build this shape?
How many sides does this new shape have?
How many vertices does this shape have?
What is the name of this new shape?
How can you check if this shape is congruent with another shape on your paper?
If you turn the shape sideways, is it congruent with another shape on your paper?
Look at all the triangles you have created. What is similar about them?
Look at all the pentagons you have created. Do they always have five sides? Do they sometimes have five congruent sides?
Look at all the rectangles you have created. Do they always have two pairs of congruent sides?
What do the square and the rectangle have in common?

Consolidation of Learning

Show all the new shapes.

Have students present their new shapes and describe their construction.

Examples

Four small orange squares were used to form a large square.
We used two green triangles to form a quadrilateral.
We used a triangle and a square to form a pentagon.

Sort, as a group, the new shapes into families of triangles, quadrilaterals, etcetera.

Ask questions such as:

What do all triangles have in common?
How can triangles differ?
What do quadrilaterals have in common?
How can quadrilaterals differ?
What is similar about pentagons?
What is different about pentagons?
How are all hexagons similar?
How can hexagons differ?
How are all heptagons similar?
How can heptagons differ?
How are all octagons similar?
How can octagons differ?

Examples of Success Criteria

The student:

builds geometric shapes;
traces the outline of the constructed geometrical shapes;
names the two-dimensional shapes corresponding to the outlines;
determines if two two-dimensional shapes are congruent by superimposing them;
indicates the congruent sides of a shape;
sorts the shapes according to the number of sides;
describes shapes according to their properties;
recognizes that all two-dimensional shapes of the same family have the same number of sides and vertices;
recognizes that shape, size, and location may change from one shape to another.

Differentiated Instruction

The activity can be modified to meet the needs of the students.

Follow-Up at Home

At home, students can identify and describe objects made up of geometric shapes (for example, the window is a large rectangle made up of two smaller rectangles).

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Géométrie et sens de l'espace, p. 147-151.

Activity 2: Lines of Symmetry

Material (per student)

Appendix 3PF.5
two copies of Appendix 3PF.6
a geoboard (5 × 5)
different coloured rubber bands
a Mira

Provide the following instructions:

construct each shape on a geoboard;
use a Mira to locate the lines of symmetry of each shape;
use different coloured rubber bands to represent each line of symmetry of the same shape;
reproduce each shape on the dot paper;
use a different colour for each line of symmetry in the same shape;
title table Lines of Symmetry.

Share by asking questions such as:

Can a triangle always have three lines of symmetry?
Can a rectangle have no (zero) line of symmetry?
Can a hexagon have four lines of symmetry?
Does a square always have four lines of symmetry?

Note: It is impossible to construct a regular pentagon, a regular hexagon or a regular octagon on a geoboard, since the distance between two points on the diagonal is greater than the distance between two points on the vertical or horizontal.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Géométrie et sens de l'espace, p. 162.

Activity 3: Symmetrical Quadrilaterals

Provide students with a copy of Appendix 3PF.6, a geoboard, rubber bands, and a Mira.

Present the following problems.

Construct a quadrilateral that has a line of symmetry.
Construct a hexagon that has no line of symmetry.
Construct two different quadrilaterals that each have two lines of symmetry.
Construct a triangle that has a line of symmetry.
Construct a two-dimensional shape that has four lines of symmetry.

In each case, ask the students to:

construct the shape on the geoboard;
use the Mira to find the lines of symmetry
reproduce the shape on the dot paper;
use a different colour for each line of symmetry in a shape.

Form teams of four students and ask them to compare the shapes they constructed for each problem.

Examples of quadrilaterals constructed in the first problem:

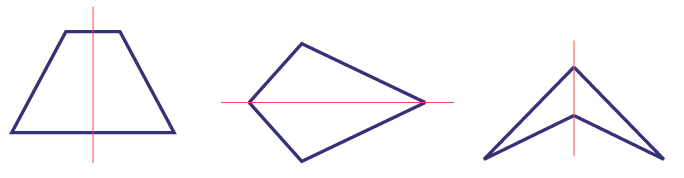
A trapezoid with a vertical axis of symmetry in red. A rhombus with the axis of symmetry placed horizontally, the axis is in red. A quadrilateral, in the shape of an arrowhead, is crossed by a red line which represent

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Géométrie et sens de l'espace, p. 162-163.

Activity 4: Drawing with Symmetry

Have students create a drawing that contains at least five of the following two-dimensional shapes: triangle, square, rectangle, other quadrilaterals, pentagon, hexagon, heptagon, and octagon.

Example

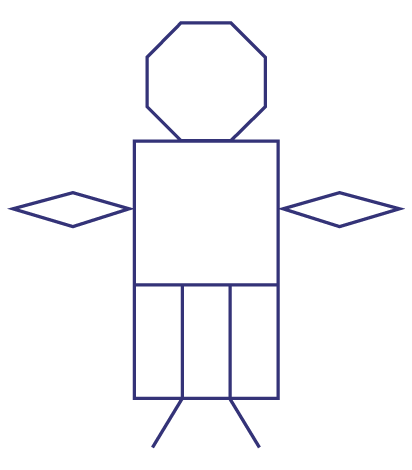
A character is represented with shapes, as follows: The head is a hexagon. The body is a square. The arms are represented by two diamonds. The legs are rectangles. Two straight lines represent the feet.

Tell students to draw all lines of symmetry for each two-dimensional shape.

Example

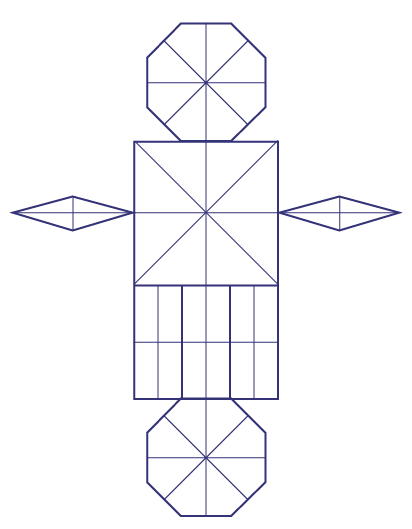
The figure formed with the shapes is represented with all the axes of symmetry of all the flat shapes that portray it.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Géométrie et sens de l'espace, p. 164-165.

To Facilitate the Task	To Enrich the Task
Have students form one shape from each family rather than several; Tell students to find the new shapes using identical shapes only (for example, two triangles to form a quadrilateral; four squares to form a bigger square; three squares to form a rectangle).	Repeat the same type of activity using tangram pieces.