E1.1 Classer et identifier des figures planes en comparant le nombre de côtés, la longueur des côtés, les angles et le nombre d’axes de symétrie.
HABILETÉ : CLASSER DES FIGURES PLANES
Classer consiste à considérer ou à concevoir des classes dans lesquelles il est possible de grouper des objets, des figures planes ou des solides qui se différencient les uns des autres et à les placer en fonction de ces classes.
En 2e année, l’élève classe et identifie des figures planes en les comparant.
Lorsque l’élève peut faire ressortir des ressemblances et des différences, elle ou il peut classer des objets, des figures planes ou des solides selon un ou des attributs (couleur, texture, etc.) en se servant par exemple de cerceaux, de boîtes ou d’un tableau à double entrée.
Dès la 2e année, l’élève pourra classer des formes géométriques selon une ou des propriétés (par exemple, nombre de côtés, longueur des côtés, angles et nombre d’axes de symétrie).
Lorsque l’élève a classé plusieurs formes selon une propriété déjà choisie, le personnel enseignant lui demande de classer des figures planes en choisissant son propre critère de classement.
Exemple
Critères de classement
- Figures planes formées d’une ligne fermée brisée
- Figures planes formées d’une ligne fermée courbe
- Figures planes qui ont trois côtés
- Figures planes qui ont quatre côtés
- Figures planes sans côtés
Au moment de l’objectivation, le personnel enseignant demande à l’élève d’expliquer, par exemple, la propriété commune à toutes les formes de la même classe, afin de l’amener à distinguer les propriétés importantes de celles qui ne le sont pas dans l’identification d’une figure plane. Il met aussi l’accent sur les mots relatifs à la certitude (par exemple, certain, impossible, possible) afin de créer des liens avec le domaine Données. Il exige que l’élève les utilise en décrivant des propriétés communes aux familles de formes géométriques, par exemple :
- Il est certain que les triangles auront trois côtés.
- Il est possible que les triangles aient un angle droit.
- Il est possible que les triangles aient trois côtés congrus.
- Il est impossible que les triangles aient quatre côtés.
Avec le temps, l’élève se rend compte que les familles de formes géométriques ont des propriétés communes (par exemple, tous les triangles ont trois côtés) et que les sous-ensembles ont des propriétés distinctes (par exemple, certains triangles ont deux côtés égaux).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 34-35.
À partir de la 2e année, le diagramme de Venn est un excellent outil pour classer les formes géométriques selon différentes propriétés. Il permet à l’élève de reconnaître les propriétés communes et distinctes des différentes familles de formes géométriques. Ce genre d’activité intègre des concepts des domaines Données et Sens de l’espace.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 18.
En se servant de diagrammes de Venn, l’élève de 2e année classe des figures planes selon un ou deux attributs. Cela lui permet d’approfondir davantage sa connaissance :
- des propriétés communes aux grandes familles des figures planes (polygones ou cercles);
- des propriétés distinctes des sous-ensembles des figures planes (par exemple, quadrilatères, pentagones).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 35-36.
Le classement des figures planes en fonction de leurs propriétés géométriques est étroitement lié à l’attente Sens de la mesure (E2). L’élève doit pouvoir utiliser des unités de mesure non conventionnelles et conventionnelles de façon appropriée pour comparer des longueurs et des angles. Par exemple, elle ou il peut utiliser la largeur de son doigt (unité de mesure non conventionnelle) ou une règle graduée en centimètres (unité de mesure conventionnelle) pour mesurer les côtés de deux figures planes et ensuite comparer les mesures pour effectuer un classement juste.
Dans le domaine Données, on peut classer ou comparer des formes géométriques à l’aide de diagrammes et décrire des propriétés des formes géométriques en utilisant des expressions de probabilité, etc.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 17.
Relations entre les classes des figures planes
Les relations entre les différentes classes de figures planes sont importantes à établir. Au primaire, les élèves apprennent les propriétés d’un rectangle, d’un carré, d’un quadrilatère et d’autres formes géométriques. À mesure que les élèves développent leur compréhension de ces propriétés, elles et ils apprennent que certaines classes sont en fait des sous-ensembles d’autres classes. Les élèves apprennent notamment que :
- les rectangles sont aussi des quadrilatères, car les deux ont quatre côtés;
- les carrés sont également des rectangles, car les deux ont quatre côtés et quatre angles droits.
Il n’est pas réaliste de s’attendre à ce que les élèves du primaire comprennent et expliquent parfaitement les relations entre les classes des figures planes. Cependant, le personnel enseignant doit veiller à ne pas classer les figures planes de façon si rigide qu’il transmet des renseignements erronés que les élèves devront « désapprendre » plus tard (Clements, 1999; Copley, 2000). Par exemple, le personnel enseignant ne devrait pas dire : « Non, ce n’est pas un rectangle, c’est un carré. »
Source : Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, p. 16.
HABILETÉ : IDENTIFIER DES FIGURES PLANES
À la maternelle et au jardin d’enfants, l’enfant reconnaît certaines formes géométriques. Elle ou il les reconnaît en les montrant du doigt et en déterminant leur nature. Dès la 1re année, l’élève peut nommer les formes géométriques découvertes à la maternelle ou au jardin d’enfants et plusieurs autres, et peut aussi indiquer la région intérieure et la région extérieure de figures planes. L’élève peut tracer à l’aide d’un pointeur, d’une baguette ou de son doigt, la ligne fermée qui entoure une figure plane et l’identifier comme étant une ligne brisée ou courbe. De même, elle ou il peut montrer les sommets et les côtés d’une figure plane ainsi que les sommets, les arêtes, les faces et les surfaces d’un solide. L’élève démontre ainsi qu’elle ou il associe le vocabulaire approprié aux éléments de la forme géométrique.
Exemple
Progression du vocabulaire relatif au concept de triangle :
|
Maternelle/ Jardin d’enfants |
1re année |
2e année |
|
C'est un triangle. |
C'est un triangle. Voici les trois sommets (en les montrant du doigt). Voici les trois côtés (en les montrant du doigt). Voici la ligne fermée brisée (en la traçant du doigt) |
Un triangle peut pointer vers la gauche, vers la droite, vers le bas ou vers le haut. Un triangle peut avoir trois côtés de différentes longueurs. |
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32-33.
HABILETÉ : COMPARER DES FIGURES PLANES
Le fait de comparer permet à l’élève de comprendre les ressemblances et les différences entre des figures planes. En observant et en manipulant une variété d’objets familiers, de représentations de figures planes (par exemple, mosaïques géométriques), l’élève y remarque d’abord les différences et les ressemblances visuelles et tactiles.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 33.
CONNAISSANCE : FIGURES PLANES
Les figures planes possèdent des propriétés géométriques qui permettent de les reconnaître, de les comparer, de les trier et de les classer.
Voici des types de figures planes qui peuvent être incluses dans les activités des élèves de 2e année.
image Un tableau qui permet de classer les figures planes, avec des exemples.Un- figures planes
concaves, avec un exemple.2- figures planes convexes : exemple de l’octogone et une autre figure.3- Figures planes ne
comportant que des lignes courbes exemple du croissant de lune.4- Figures planes comportant des ligne3s courbes et des
lignes droites, exemple d’un trois-quarts de cercle.5-Figures planes régulières (parenthèse ouvrante) figures ayant
des côtés et des angles congrus (parenthèse fermante). Exemple d’un hexagone.6- Figures irrégulières (parenthèse
ouvrante) figures ayant les côtés de différentes longueurs et des angle3s différents (parenthèse fermante). Il y a un
exemple.7-Deux figures planes ayant des côtés de la même longueur, mais des angles différents. Les exemples sont un
rectangle et un parallélépipède.8-Figures planes ayant les côtés de différentes longueurs, mais les angles congrus.
L’exemple est un rectangle.9- Figures planes non symétriques. Il y a un exemple.Dix- Figures symétriques. L’exemple
est un cœur. L’axe de symétrie est dessiné avec une ligne pointillée.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : NOMBRE DE CÔTÉS
Les élèves de 2e année peuvent reconnaître des figures planes, des triangles (trois côtés) jusqu’aux octogones (huit côtés), dont des polygones réguliers et irréguliers.
CONNAISSANCE : LONGUEUR DES CÔTÉS
La longueur est le terme général utilisé pour désigner toute grandeur d’un espace à une dimension que l’on mesure à l’aide d’un objet étalon.
Une longueur peut désigner :
- la grandeur d’un segment, c’est-à-dire la distance entre deux points;
- la distance entre deux droites parallèles ou deux plans parallèles;
- un périmètre;
- une hauteur, une profondeur, une épaisseur, une largeur, une taille (d’une personne).
Note : Pour certaines et certains élèves, ces différents termes associés à la longueur peuvent prêter à confusion. Le terme « grandeur » utilisé dans la description des attributs longueur, aire et capacité désigne ce qui peut être estimé, évalué ou mesuré.
Exemples
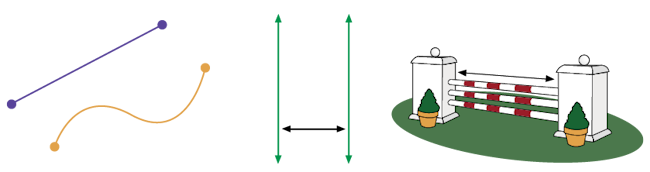image Deux points reliés par une droite.Deux points reliés par une ligne
courbe.Deux doubles flèches, vertes. Elles sont parallèles. Entre elles est placée une double flèche noire, elle se
place perpendiculairement par rapport aux autres doubles flèches.Un obstacle pour les chevaux. Une flèche est placée
entre les deux socles verticaux.
La longueur d’un livre devient sa hauteur lorsqu’on le range debout sur une étagère, tout comme son épaisseur devient sa largeur.
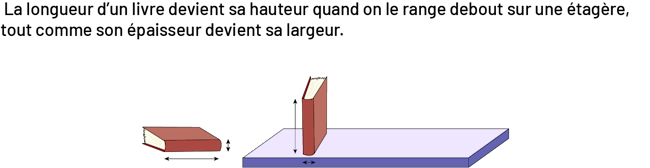image Deux livres. Le premier livre est déposé sur le plat de sa couverture. Une flèche montre la
longueur du livre et une autre flèche montre son épaisseur.Le second livre est debout sur une étagère, une flèche
montre sa hauteur et une seconde flèche montre son épaisseur.
Source : Fiche de la maternelle à la 3e année Attribut longueur, p. 2.
CONNAISSANCE : ANGLES
Un angle désigne l’amplitude d’une « ouverture ».
Un angle peut être formé ou déterminé par :
- deux droites de même origine;
- deux demi-plans qui se croisent;
- une rotation autour d’un point.
Exemples
Angle formé par deux demi-droites de même origine.
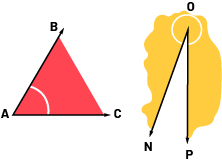
Angle formé par deux demi-plans qui se croisent.
Source : Fiche de la 4e à la 6e année Attribut angle, p. 2.
CONNAISSANCE : NOMBRE D’AXES DE SYMÉTRIE
Une figure a une symétrie de réflexion si une moitié de la figure est une réflexion de l’autre moitié par rapport à un axe appelé l’axe de symétrie. Les figures peuvent avoir un ou plusieurs axes de symétrie.
- Un axe de symétrie
- Deux axes de symétrie (ou plus)
- Aucun axe de symétrie
Les élèves de 2e année peuvent :
- reconnaître des exemples de symétrie dans leur environnement, entre autres des formes dont l’axe est non vertical;
- dessiner des formes symétriques ou en créer à l’aide de matériel concret;
- déterminer l’axe de symétrie de formes à deux dimensions. Les élèves reconnaissent facilement les axes verticaux, mais peuvent avoir du mal à repérer les axes de symétrie non verticaux.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 7