E1.1 Sort and identify two-dimensional shapes by comparing number of sides, side lengths, angles, and number of lines of symmetry.
Skill: Sorting Two-Dimensional Shapes
Sorting requires one group objects, two-dimensional shapes, or three-dimensional objects according to attributes or characteristics .
When students identify similarities and differences, they can sort objects, two-dimensional shapes, or three-dimensional objects by attribute(s) (colour, texture, etcetera) using organizers such as hoops, boxes, or a double entry table.
By Grade 2, students will be able to sort geometric shapes according to one or more properties (for example, number of sides, length of sides, angles, and number of lines of symmetry).
Once students have classified several two-dimensional shapes according to one property, teachers can ask them to classify two-dimensional shapes by choosing their own classification criteria.
Example
Sorting rules
- Two-dimensional shapes formed by a broken closed line
- Two-dimensional shapes formed by a closed curved line
- Two-dimensional shapes that have three sides
- Two-dimensional shapes that have four sides
- Two-dimensional shapes without sides
During consolidation, teachers should support students to identify the properties that are common to all shapes in the same class. This will help them distinguish those properties that are important in identifying a two-dimensional shape. Teachers can also emphasize words related to likelihood (for example, certain, impossible, possible) to make connections to the Data strand. For example:
- It is certain that triangles have three sides.
- It is possible that triangles have a right angle.
- It is possible that triangles have three congruent sides.
- It is impossible for triangles to have four sides.
Over time, the students realize that families of geometric shapes have common properties (for example, all triangles have three sides) and that subsets have distinct properties (for example, some triangles have two equal sides).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 34-35.
Beginning in Grade 2, the Venn diagram is an excellent tool for sorting geometric shapes according to different properties. Students can use them to classify two-dimensional shapes according to one or two attributes. This allows them to further develop their knowledge of:
- properties common to the large families of two-dimensional shapes (polygons or circles);
- distinct properties of subsets of two-dimensional shapes (for example, quadrilaterals, pentagons).
Closely related to expectation E2 Measurement is the sorting of two-dimensional shapes according to their geometric properties. Students must be able to use non-standard and standard units of measurement appropriately to compare lengths and angles. For example, they may use the width of their finger (non-standard unit) or a ruler graduated in centimeters (standard unit) to measure the sides of two two-dimensional shapes and then compare the measurements to make a sort.
In the Data strand, one can sort or compare geometric shapes using graphs and describe properties of geometric shapes using probability expressions.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 17.
Relationships Between the Classes of Two-Dimensional Shapes
The relationships between different classes of two-dimensional shapes are important to establish. In elementary school, students learn the properties of a rectangle, square, quadrilateral, and other geometric shapes. As students develop their understanding of these properties, they learn that some classes are actually subsets of other classes. In particular, students learn that:
- rectangles are also quadrilaterals, because both have four sides;
- squares are also rectangles, because both have four sides and four right angles.
It is unrealistic to expect elementary students to fully understand and explain the relationships between classes of two-dimensional shapes; however, teachers must be careful not to sort two-dimensional shapes so rigidly that they convey misinformation that students will have to “unlearn” later (Clements, 1999; Copley, 2000). For example, the teacher should not say, “No, this is not a rectangle, it is a square.”
Source: translated from Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, Géométrie et sens de l'espace, p. 16.
Skill: Identifying Two-Dimensional Shapes
In Kindergarten, children begin to describe, sort, classify, build and compare two-dimensional shapes and three-dimensional figures by exploring, and comparing their attributes and properties. For example, they might point to a triangle and say that it has three sides. In Grade 1, students begin to name geometric shapes and their features, such as the vertices and sides of a two-dimensional shape and the vertices, edges, faces, and surfaces of a three-dimensional object. In this way, students demonstrate that they are able to associate the appropriate vocabulary with the elements of a geometric form. In Grade 2, students begin to identify the characteristics of two-dimensional shapes, and can begin to compare shapes by considering number of sides, side lengths, angles, and number of lines of symmetry.
Example
Progression of vocabulary related to the concept of a triangle:

|
Kindergarten/ Nursery School |
Grade 1 |
Grade 2 |
|
It is a triangle. |
This is a triangle. Here are the three vertices (pointing to them). Here are the three sides (pointing with your finger). Here is the broken closed line (by drawing it with your finger) |
A triangle can point left, right, down or up. A triangle can have three sides of different lengths. |
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 32-33.
Skill: Comparing Two-Dimensional Shapes
By observing and manipulating a variety of familiar objects and representations of two-dimensional shapes (for example, pattern blocks), students first notice visual and tactile differences and similarities.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 33.
Knowledge: Two-Dimensional Shapes
Two-dimensional shapes have geometric properties that allow them to be identified, compared, sorted, and classified.
The following are types of two-dimensional shapes that can be included in Grade 2 student activities.
 image A table that classifies flat shapes, with examples. 1- flat concave shapes, with an example. 2- Flat convex shapes: example of the octagon and another shape. 3- Flat shapes with only curved lines: example of the crescent moon. 4- Flat shapes with curved lines and straight lines, example of a three-quarter circle. 5-Regular flat shapes (opening parenthesis) figures with congruent sides and angles (closing parenthesis). Example of a hexagon. 6- Irregular shapes ( open parenthesis) shapes with different lengths of sides and different angles (close parenthesis). There is an example. 7-Two flat shapes with sides of the same length, but different angles. The examples are a rectangle and a parallelepiped. 8-Flat shapes with different side lengths, but congruent angles. The example is a rectangle. 9- Non-symmetrical flat shapes. There is an example. 10- Symmetrical shapes. The example is a heart. The axis of symmetry is drawn with a dotted line.
image A table that classifies flat shapes, with examples. 1- flat concave shapes, with an example. 2- Flat convex shapes: example of the octagon and another shape. 3- Flat shapes with only curved lines: example of the crescent moon. 4- Flat shapes with curved lines and straight lines, example of a three-quarter circle. 5-Regular flat shapes (opening parenthesis) figures with congruent sides and angles (closing parenthesis). Example of a hexagon. 6- Irregular shapes ( open parenthesis) shapes with different lengths of sides and different angles (close parenthesis). There is an example. 7-Two flat shapes with sides of the same length, but different angles. The examples are a rectangle and a parallelepiped. 8-Flat shapes with different side lengths, but congruent angles. The example is a rectangle. 9- Non-symmetrical flat shapes. There is an example. 10- Symmetrical shapes. The example is a heart. The axis of symmetry is drawn with a dotted line.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Number of Sides
Grade 2 students can identify two-dimensional shapes, from triangles (three sides) to octagons (eight sides), including regular and irregular polygons.
Knowledge: Length of the Sides
Length is a measure in a one-dimensional space (for example, height, depth, width, thickness, radius, diameter). The perimeter is the length around a two-dimensional shape or of any three-dimensional object.
A length can refer to:
- the size of a line segment, namely. the distance between two points;
- the distance between two parallel lines or two parallel planes;
- a perimeter;
- a height, a depth, a thickness, a width, a height (of a person).
Note: For some students, these different terms associated with length may be confusing.
Examples
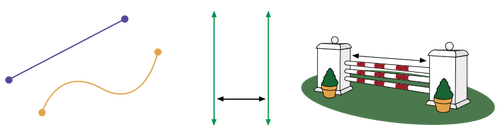 image Two points connected by a straight line. Two points connected by a curved line. Two double arrows, green. They are parallel. Between them is a black double arrow, it is perpendicular to the other double arrows. An obstacle for the horses. An arrow is placed between the two vertical bases
image Two points connected by a straight line. Two points connected by a curved line. Two double arrows, green. They are parallel. Between them is a black double arrow, it is perpendicular to the other double arrows. An obstacle for the horses. An arrow is placed between the two vertical bases
The length of a book becomes its height when stored upright on a shelf, just as its thickness becomes its width.
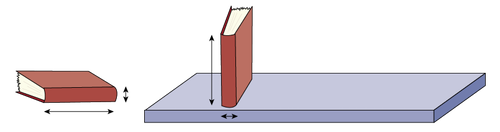
Source: translated from Fiche de la maternelle à la 3e année Attribut longueur, p. 2.
Knowledge: Angles
A shape formed by two rays or two line segments with a common endpoint.
An angle can be formed or determined by:
- two lines of the same origin;
- two intersecting half-planes;
- a rotation of a line segment around a fixed point.
Examples
Angle is the measure of turn between two rays or line segments with a common endpoint.
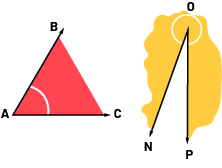
Angle formed by two intersecting half-planes.

Source: translated from Fiche de la 4e à la 6e année Attribut angle, p. 2.
Knowledge: Number of Lines of Symmetry
A two-dimensional shape has line symmetry if the shape can be divided into two congruent parts that can be matched by folding along a line, known as the line of symmetry.
Shapes can have:
- A line of symmetry
- Two or more lines of symmetry
- No line of symmetry
Grade 2 students may:
- identify examples of symmetry in their environment, including shapes with non-vertical lines of symmetry;
- draw or create symmetric shapes using concrete materials;
- determine the line of symmetry of two-dimensional shapes. Students easily recognize vertical lines of symmetry, but may have difficulty locating non-vertical lines of symmetry.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 7
