E1.3 Identifier des longueurs et des angles congrus dans des figures planes en les superposant mentalement et concrètement, et déterminer si les figures planes sont congruentes.
HABILETÉ : DÉTERMINER LA CONGRUENCE DE DEUX FIGURES PLANES
La congruence est une relation particulière entre des figures planes dont les mesures de tous les éléments correspondants (côtés et angles) sont égales. Les élèves de 2e année explorent et construisent le concept des « figures planes régulières » – une figure dont les côtés et les angles sont tous congrus. À ce moment, les élèves découvrent que celles-ci « se ressemblent en tous points » en les superposant les unes sur les autres pour voir à quel point elles correspondent.
Les élèves du cycle primaire rencontreront souvent des concepts liés à la congruence en géométrie notamment :
- les faces d’un solide peuvent être congruentes (par exemple, les faces d’un cube sont des carrés congruents; les deux bases d’un prisme à base pentagonale sont en forme de pentagones congruents);
- les translations (déplacer une forme) et les réflexions (faire refléter une forme comme dans un miroir) donnent une image congruente à la figure initiale.
Source : Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, p. 18.
HABILETÉ : IDENTIFIER DES LONGUEURS CONGRUES
Les élèves superposent deux figures planes pour déterminer si la longueur des côtés est congrue. Par exemple, les élèves construisent deux triangles à l’aide d’un géoplan.
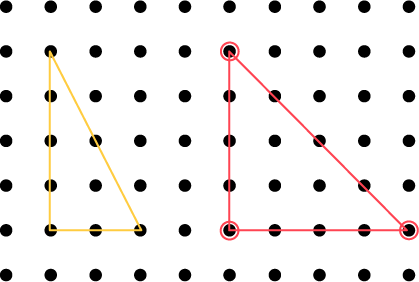
En les superposant, les élèves remarquent que la mesure de la longueur d’un seul côté est congrue, soit la mesure du côté AB.
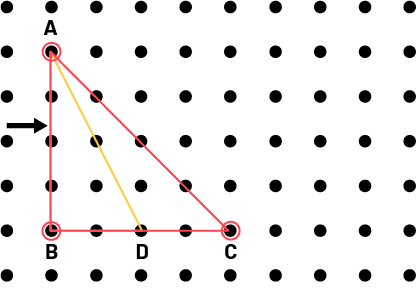
HABILETÉ : IDENTIFIER DES ANGLES CONGRUS
Les élèves superposent deux figures planes pour déterminer si les angles sont congrus. Par exemple, les élèves construisent deux triangles à l’aide d’un géoplan.

En les superposant, les élèves remarquent que les angles B sont congrus. Les angles A ne sont pas congrus.
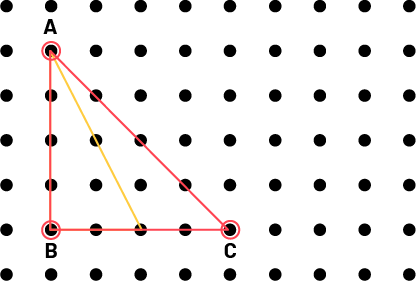
Une autre superposition est nécessaire pour vérifier si les angles C sont congrus. Les angles C ne sont pas congrus.
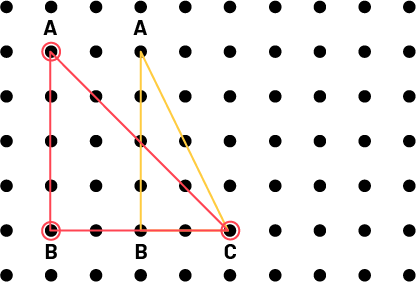
CONNAISSANCE : CONGRU
Lorsque les mesures de deux angles ou deux segments de droite sont égales, les deux angles ou les deux segments de droite sont congrus.
Source : Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, p. 18.
CONNAISSANCE : CONGRUENCE
Lorsque les mesures de tous les éléments correspondants (côtés et angles) sont égales, les deux figures planes sont congruentes.
Source : Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, p. 18.
