E1.3 Identify congruent lengths and angles in two-dimensional shapes by mentally and physically matching them, and determine if the shapes are congruent.
Skill: Determining the Congruence of Two Two-Dimensional Shapes
Congruence is a special relationship between two-dimensional shapes whose measures of all corresponding elements (sides and angles) are equal. Grade 2 students explore and construct the concept of ”regular two-dimensional shapes“ - a shape whose sides and angles are all congruent. At this point, students discover that these ”look the same in every way“ by superimposing them on top of each other to see how well they match.
Elementary students will often encounter concepts related to congruence in geometry, including:
- the faces of a three-dimensional object can be congruent (for example, the faces of a cube are congruent squares; the two bases of a pentagon-based prism are congruent pentagons);
- translations (moving a shape) and reflections (reflecting a shape as in a mirror) give an image congruent to the initial shape.
Source: translated from Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, Géométrie et sens de l'espace, p. 18.
Skill: Identifying Congruent Lengths
Students superimpose two two-dimensional shapes to determine if the side lengths are congruent. For example, students construct two triangles using a geoboard.
By superimposing them, students notice that the measure of the length of only one side is congruent, which is the measure of side AB.
image A geoplane where two rubber bands, one yellow and one red, are shaped like a triangle. They are superimposed to show their differences. The first triangle is called, "A", "B", "D". The second triangle is called "A", "B", "C". An arrow points to side "A". The arrow points to the side of "B" that is common to both triangles.
Skill: Identifying Congruent Angles
Students superimpose two two-dimensional shapes to determine if the angles are congruent. For example, students construct two triangles using a geoboard.
By superimposing them, students notice that angles B are congruent; angles A are not congruent.
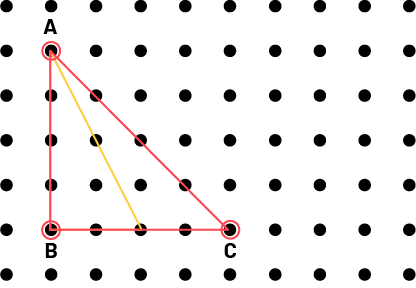
Another superimposition is needed to check if the angles C are congruent. The angles C are not congruent.
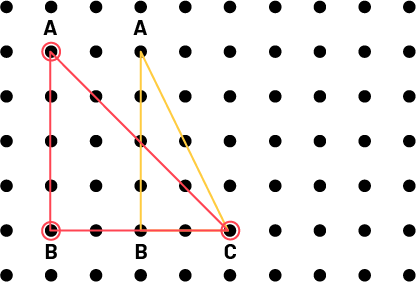
Knowledge: Congruent
When the measurements of two angles or two line segments are equal, the two angles or the two line segments are congruent.
When the measurements of all corresponding elements (sides and angles) are equal, the two two-dimensional shapes are congruent
Source: translated from Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, Géométrie et sens de l'espace, p. 18.