E1.1 Classer, construire et identifier des cubes, des prismes, des pyramides, des cylindres et des cônes en comparant les faces, les sommets, les arêtes et les angles.
HABILETÉ : IDENTIFIER DES CUBES, DES PRISMES, DES PYRAMIDES, DES CYLINDRES ET DES CÔNES
De la 1re à la 3e année, l’élève doit continuellement redéfinir l’image mentale qu’elle ou il se fait d’une figure plane ou d’un solide, car sa représentation mentale est souvent limitée à celle qu’on lui présente le plus souvent ou à une représentation stéréotypée. Une variété de représentations des formes géométriques aide l’élève à comprendre l’invariance des propriétés de la forme, peu importe le matériau, la taille, l’orientation, la perspective, etc. Par exemple, toute forme à deux dimensions ayant quatre côtés congrus et quatre côtés droits est un carré.
Il importe donc que, lors d’activités dirigées ou partagées de mathématiques, le personnel enseignant profite de l’occasion pour présenter une grande variété de représentations :
- de photos d’objets sous diverses perspectives;
- de dessins d’objets à trois dimensions reproduits de façons différentes.
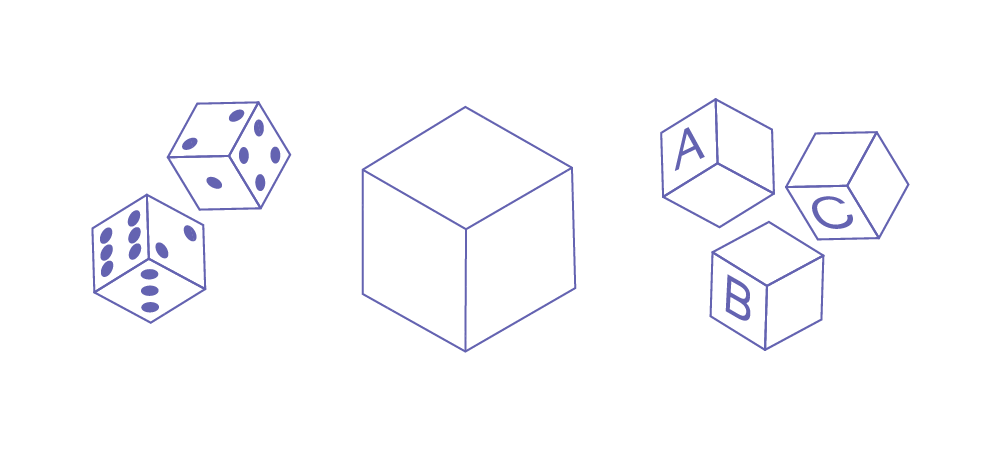
Quelques enfants peuvent se représenter certaines figures planes et certains solides, mais ne sont pas encore capables d’opérations réversibles. Dès que l’on modifie, par exemple, l’orientation d’un rectangle ou d’un cylindre, elles et ils ont tendance à penser que ce n’est plus la même figure ou le même solide. L’enfant ne comprend pas que certaines modifications topographiques ne changent pas la figure plane ou le solide même.
Exemple
Quelques élèves croient que le premier cylindre est un bon cylindre, alors que le second est un mauvais cylindre, puisque l’image mentale qu’elles et ils ont du cylindre correspond à celle d’un cylindre déposé sur sa base. Il faut donc les amener à réaliser qu’un cylindre reste un cylindre, même s’il est placé différemment. Le solide a toujours une face plane en forme de cercle et une surface courbe.
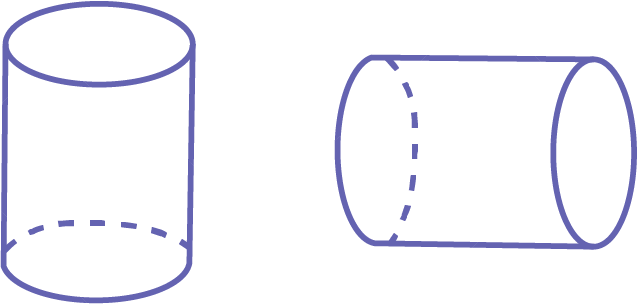
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 36-37.
HABILETÉ : CLASSER DES SOLIDES
En 3e année, l’élève classe, construit et nomme des solides.
Lorsque l’élève peut faire ressortir des ressemblances et des différences, elle ou il peut classer des objets, des figures planes ou des solides selon un attribut en se servant, par exemple, de deux cerceaux, de deux boîtes ou d’un tableau à double entrée.
Dès la 2e année, l’élève pourra classer des formes géométriques selon une propriété (par exemple, nature de la forme, nombre de sommets, nombre d’axes de symétrie).
Exemple
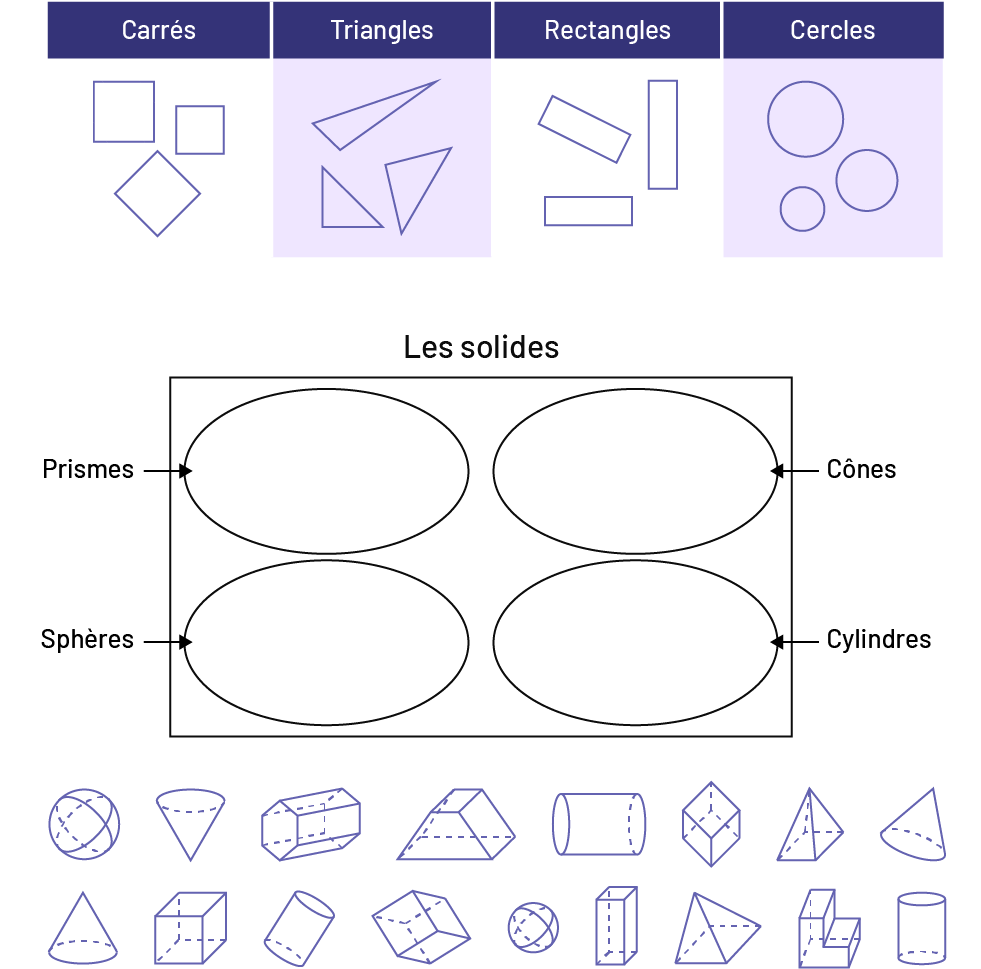Image La première image est un tableau qui contient des illustrations de :
« carrés » « triangles », « rectangles,
» et « cercles. » La deuxième image est un diagramme de Venn. Un rectangle nommé « les solides », contient 4 ovales,
ils sont
respectivement nommés : respectivement : « cubes, » « cônes» « sphères, » « cylindres. » Sous le diagramme de Venn, on
retrouve deux rangées de solides. La première rangée: « sphère, » « cône, » « prisme
à base hexagonale, » « polyèdre, » « cylindre, » « cube, « « pyramide à base rectangulaire, » « cône. » Deuxième
rangée: « cône, » « cube, » « cylindre, » « cube, » « sphère, » « prisme rectangulaire à base carré, » « pyramide à
base carrée, » « polyèdre, » « cylindre, »
Lorsque l’élève a classé plusieurs formes selon un critère déjà choisi, le personnel enseignant lui demande de classer des figures planes ou des solides à l’aide de son propre critère de classement.
Exemple
Critères de classement
- Solides qui ont seulement des faces.
- Solides qui ont des faces et des surfaces.
- Solides qui ont seulement des surfaces.
Lors de l’objectivation, le personnel enseignant demande à l’élève d’expliquer, par exemple, la propriété commune à toutes les formes de la même classe, afin de l’amener à distinguer les propriétés importantes de celles qui ne le sont pas dans l’identification d’une figure plane ou d’un solide. L’élève met aussi l’accent sur les mots relatifs à la probabilité (par exemple, impossible, peu probable, équiprobable, très probable et certain) afin de créer des liens avec le domaine Données. Il exige que l’élève les utilise en décrivant des propriétés communes aux familles de formes géométriques. Par exemple, « Il est impossible qu’un solide soit à la fois une pyramide et une sphère. », « Il est certain que tous les prismes ayant des carrés comme base s’appellent des prismes à base carrée. », « Il est peu probable qu’un solide roule, il est très probable qu’un solide puisse glisser. ».
Avec le temps, l’élève se rend compte que les familles de formes géométriques ont des propriétés communes (par exemple, tous les prismes ont deux bases congruentes) et que les sous-ensembles ont des propriétés distinctes (par exemple, tous les prismes ayant des triangles comme bases s’appellent des prismes à base triangulaire).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 34-35.
Le diagramme de Venn est un excellent outil pour classer les formes géométriques selon différentes propriétés. Il permet à l’élève de reconnaître les propriétés communes et distinctes des familles de formes géométriques. Ce genre d’activité intègre des concepts en Données et en Sens de l’espace.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 18.
En se servant de diagrammes de Venn, l’élève de 3e année classe des solides selon deux propriétés. Cela lui permet d’approfondir davantage sa connaissance :
- des propriétés communes aux grandes familles des solides (polyèdres ou corps ronds);
- des propriétés distinctes des sous-ensembles des solides (par exemple, prismes, pyramides).
Exemple
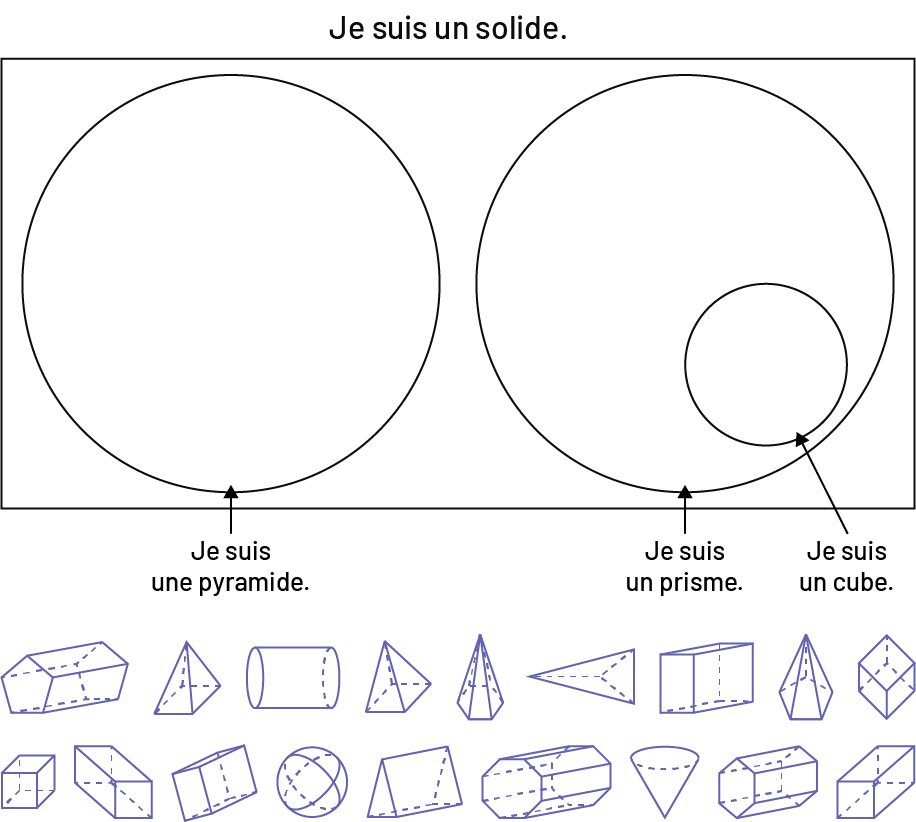Image Diagramme de Venn nommé: « Je suis un solide. » Dans un rectangle, deux grands cercles nommés respectivement
: « Je suis une pyramide, » et « Je suis un prisme. » À l’intérieur du deuxième cercle est un petit cercle nommé: «
Je suis un cube. » Sous le diagramme, il y a deux rangées de solides. La première rangée: « prisme à base
pentagonale, » « pyramide à base rectangulaire, » « cylindre, » « pyramide à base carrée, » « Pyramide à base
hexagonale, » « pyramide à base triangulaire, » « prisme rectangulaire à base rectangulaire, » « pyramide à base
pentagonale, » « cube. » La deuxième rangée: « cube, » « Prisme rectangulaire à base carré, » « prisme rectangulaire
à base rectangulaire, » « sphère, » « prisme triangulaire à base rectangulaire, » « prisme à base octogonale, « «
cône, » « prisme à base hexagonale, » « prisme rectangulaire à base carré. »
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 35-36.
HABILETÉ : CONSTRUIRE DES SOLIDES
Les activités de construction, d’assemblage et de décomposition aident l’élève à comprendre plusieurs concepts relatifs au raisonnement géométrique. Par exemple, l’élève approfondit sa compréhension des concepts d’arête et de sommet en construisant des charpentes de solides, et sa compréhension du concept de face en construisant leurs coquilles.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 40.
CONNAISSANCE : PRISME
- Les prismes ont deux faces polygonales. Ces deux faces forment la base du solide. (À noter qu’une base ne correspond pas nécessairement au « bas » du prisme.)
- Les deux bases sont liées par des rectangles ou des parallélogrammes de même hauteur (les bases sont parallèles).
- Le nom d’un prisme désigne la forme de sa base. Par exemple, le prisme à base triangulaire a deux bases qui sont des triangles, reliées par des rectangles ou des parallélogrammes.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : CUBE
- Les cubes ont six faces congruentes, et chaque face est un carré.
- Comme les cubes possèdent toutes les propriétés d’un prisme, ils peuvent également être appelés prismes à base carrée.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : CYLINDRE
- Les cylindres ont deux bases congruentes. Il est possible de relier une base à l’autre en traçant des lignes droites de longueur égale.
- Le nom d’un cylindre désigne la forme de sa base. Par exemple, une boîte de conserve est un cylindre à base circulaire.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PYRAMIDE
- Les pyramides ont une seule base qui est un polygone.
- Les faces triangulaires sont reliées à la base et se rejoignent à un sommet, l’apex.
- Le nom d’une pyramide désigne la forme de sa base. Par exemple, une pyramide à base carrée a un carré pour base et quatre faces triangulaires.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : CÔNE
- Les cônes ont une seule base. Il est possible de relier n’importe quel point du contour de la base à son sommet, l’apex, en traçant des lignes droites.
- Le nom d’un cône désigne la forme de sa base. Par exemple, un cornet de crème glacée est un cône à base circulaire.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.