E1.1 Sort, construct, and identify cubes, prisms, pyramids, cylinders, and cones by comparing their faces, edges, vertices, and angles.
Skill: Identifying Cubes, Prisms, Pyramids, Cylinders and Cones
A student's mental image of a two-dimensional shape or three-dimensional object is often limited to the one most often presented or to a stereotypical representation. A variety of representations of geometric shapes helps students understand the invariance of shape properties, regardless of material, size, orientation, perspective, etc. For example, any two-dimensional shape with four congruent sides and four straight sides is a square, regardless of its orientation.
It is important, therefore, that during guided or shared mathematics activities, teachers take the opportunity to present a wide variety of representations of:
- photos of objects from various perspectives;
- drawings of three-dimensional objects reproduced in different ways.
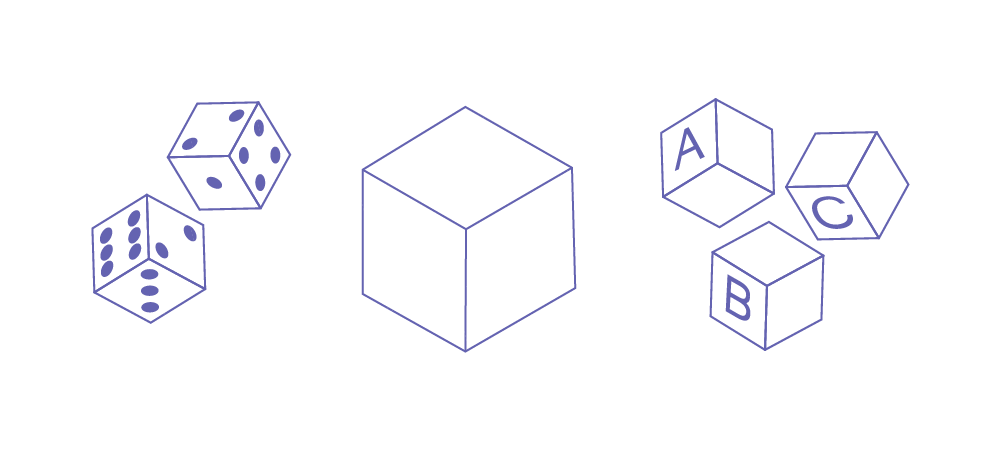
Some children can represent certain two-dimensional shapes and three-dimensional objects but are not yet capable of reversible operations. As soon as the orientation of a rectangle or cylinder is changed, for example, they tend to think that it is no longer the same two-dimensional shape or three-dimensional object. The child does not understand that certain topographical changes do not change the two-dimensional shape or three-dimensional object itself.
Example
Some students believe that the first cylinder is a proper cylinder, while the second is a wrong cylinder, since their mental image of the cylinder is that of a cylinder placed on its base. They may need to be supported to recognize that a cylinder is still a cylinder, even if it is placed differently. It always has two flat circle faces and a curved surface. It always has a flat face in the shape of a circle and a curved surface.
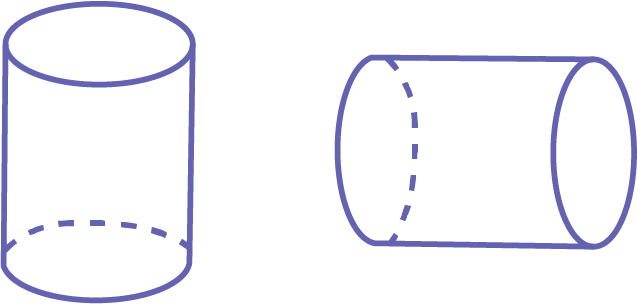
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 36-37.
Skill: Sorting Three-Dimensional Objects
In Grade 3, students will sort, construct and name three-dimensional objects.
When students can identify similarities and differences, they can sort objects, two-dimensional shapes, or three-dimensional objects according to an attribute using two hoops, two boxes, or a double entry table.
Example
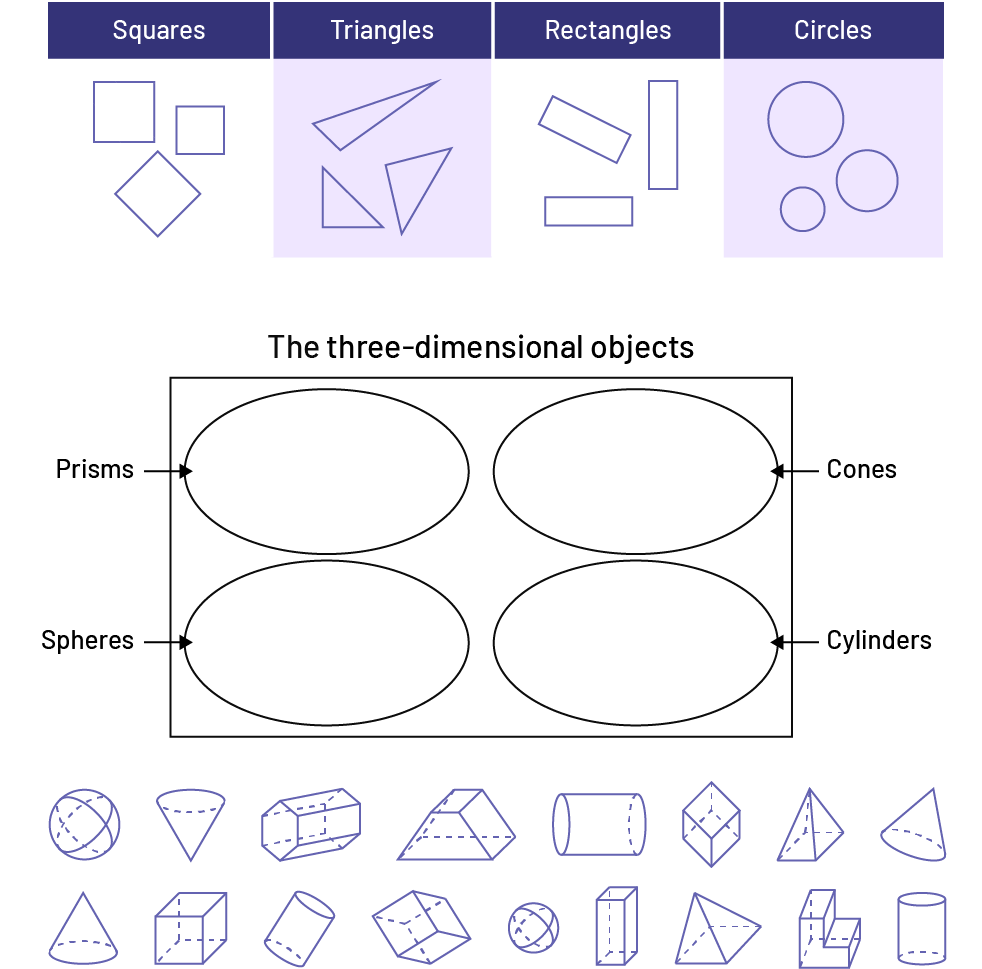The first image is a table that contains illustrations of: squarestriangles,rectangles,"
and circles. The second picture is a Venn diagram. A rectangle labeled solids", contains 4 ovals, they are
respectively labeled:
cubes,conesspheres,cylinders. Below the Venn diagram, there are two rows of solids. The first row:
sphere, cone, hexagonal based prism,
polyhedron, cylinder, cube, rectangular based pyramid, cone. Second row: cone, cube,
cylinder, cube, sphere, square-based rectangular prism, square-based pyramid, polyhedron,
cylinder,
Once the student has classified several shapes using a previously selected criterion, teachers will ask the student to sort two-dimensional shapes or three-dimensional objects using their own sorting rule.
Example
Sorting rules
- Three-dimensional objects that have only faces.
- Three-dimensional objects that have faces and curved surfaces.
- Three-dimensional objects that have only curved surfaces.
During consolidation, the teacher should ask the students questions that focus on properties common to a group of two-dimensional shapes or three-dimensional objects to support them in determining the distinguishing properties of each. The teacher could also emphasize words relating to probability (for example, impossible, unlikely, equally probable, very probable and certain) to and ask students to use them in describing properties common to families of geometric shapes. For example, “It is impossible for a three-dimensional object to be both a pyramid and a sphere.”, “It is certain that all prisms having squares as bases are called square-based prisms.”, “It is unlikely that a prism rolls, it is very probable that a prism can slide“.
Over time, the student realizes that families of geometric shapes have common properties (for example, all prisms have two congruent bases) and that subsets have distinct properties (for example, all prisms with triangles as bases are called triangle-based prisms).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 34-35.
The Venn diagram is an excellent tool for classifying geometric shapes according to different properties. It allows the student to recognize common and distinct properties of families of geometric shapes. This type of activity integrates concepts in Data and Spatial Sense.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 18.
In Grade 3 students should have opportunities to sort, using a Venn diagram, three-dimensional objects according to two properties to further develop their knowledge of:
- properties common to the large families of three-dimensional objects (polyhedron or non-polyhedron);
- distinct properties of subsets of three-dimensional objects (for example, prisms, pyramids).
Example
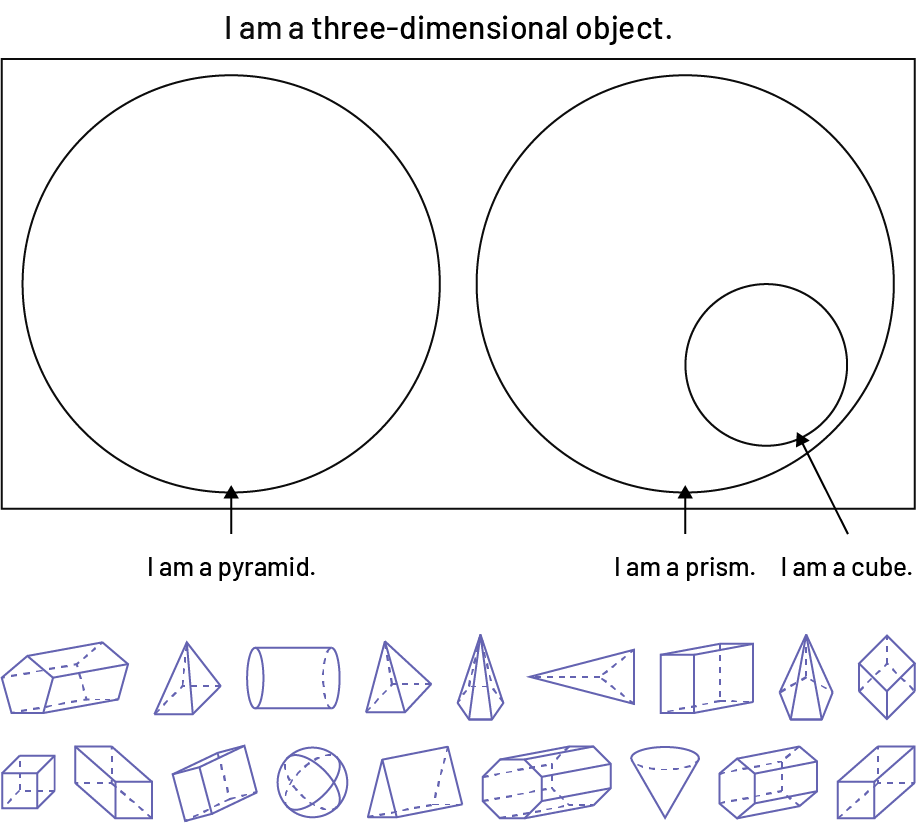Image A Venn diagram labeled: I am a solid. Inside a rectangle are two large circles labeled
respectively: I am a pyramid, and I am a prism. Inside the second circle is a small circle labeled: I am a cube."
Below the diagram, there are two rows of solids. The first row: pentagonal-based prism,rectangular-based pyramid,"
cylinder,square-based pyramid,hexagonal-based pyramid,triangular-based pyramid,rectangular-based prism,"
pentagonal-based pyramid,cube. The second row: cube, square-based rectangular prism, rectangular-based
prism, sphere, rectangular-based triangular prism, octagonal-based prism, cone, hexagonal-based
prism, square-based rectangular prism."
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 35-36.
Skill: Constructing Three-Dimensional Objects
Construction, assembly, and decomposition activities help students understand several concepts related to geometric reasoning. For example, students deepen their understanding of edges and vertices by building three-dimensional objects from nets, and their understanding of the faces by tracing their sides.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 40.
Knowledge: Prism
- Prisms have two polygonal faces. These two faces form the bases of the three-dimensional object. (Note that a base does not necessarily correspond to the ”bottom“ of the prism.)
- The two bases are linked by rectangles or parallelograms of the same height (the bases are parallel).
- The name of a prism refers to the shape of its base. For example, the triangle-based prism has two bases that are triangles, connected by rectangles or parallelograms.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Cube
- The cubes have six congruent faces, and each face is a square.
- Since cubes have all the properties of a prism, they can also be called square-based prisms.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Cylinder
- Cylinders have two congruent bases, and it is possible to connect one base to the other by drawing straight lines of equal length.
- The name of a cylinder refers to the shape of its base. For example, a tin can is a cylinder with a circular base.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Pyramid
- Pyramids have a single base which is a polygon.
- The triangular faces are connected at the base and meet at a vertex, the apex.
- The name of a pyramid refers to the shape of its base. For example, a square-based pyramid has a square base and four triangular faces.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Cone
- Cones have a single base, and it is possible to connect any point on the base contour to its apex by drawing straight lines.
- The name of a cone refers to the shape of its base, for example, an ice cream cone is a cone with a circular base.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.