E2.1 Utiliser des unités de mesure de longueur appropriées pour estimer, mesurer et comparer les périmètres de polygones et de lignes courbes fermées, et construire des polygones ayant un périmètre donné.
Habileté : utiliser des unités de longueurs appropriées
- L’unité de longueur appropriée dépend de la raison pour laquelle un objet est mesuré. Les grandes unités servent à effectuer des mesures approximatives, alors que les petites unités servent à effectuer des mesures précises. Les unités de mesure non conventionnelles conviennent aux mesures rapides et particulières. Les unités conventionnelles servent à présenter les mesures effectuées.
- La mesure d’une quantité continue, comme la longueur, est toujours approximative. Plus l’unité utilisée est petite, plus la mesure sera exacte. Si des unités de différentes grandeurs sont utilisées pour mesurer un objet, chaque unité est dénombrée et traitée séparément.
- Comme les mesures sont approximatives, une combinaison d’unités en améliorera l’exactitude (par exemple, on peut utiliser des centimètres et des millimètres pour mesurer une longueur située entre 5 et 6 cm).
Utiliser différentes unités de mesure non conventionnelles et conventionnelles
Unités non conventionnelles
- Pas
- Longueur d’enjambées
- Nombre de trombones
- Longueur de crayon
Unités de mesure conventionnelles
- Millimètre (mm)
- Centimètre (cm)
- Kilomètre (km)
Utiliser différents instruments de mesure et outils
- Ficelle
- Règle, mètre, ruban à mesurer
- Roue à mesurer
Remarque
En 3e année, les élèves n’utilisent pas de nombres décimaux pour mesurer.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
HABILETÉ : ESTIMER UNE LONGUEUR, LE PÉRIMÈTRE
Le périmètre d’un objet ou d’une région est la longueur totale de son contour ou de sa périphérie, respectivement. La mesure d’un périmètre est la mesure d’une longueur.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
« Pour certains, estimer n’est rien de plus que deviner […]. Cependant, associer l’estimation au simple fait de deviner, c’est nier le raisonnement qui la sous-tend. Formuler une estimation précise requiert souvent le recours à des stratégies de résolution de problèmes complexes et à l’application judicieuse de principes mathématiques. »
(Hodgson, Simonsen, Luebeck et Andersen, 2003, p. 226, traduction libre)
Les adultes, tout comme les élèves, doivent déterminer des grandeurs de façon approximative dans une variété de situations quotidiennes. Autrement dit, elles et ils doivent estimer des mesures (par exemple, estimer le nombre de petits trombones qu’il faut pour mesurer le contour, soit le périmètre de la table). En mesure, estimer est un processus fondé sur des renseignements visuels et sur des expériences antérieures qui permet de porter un jugement par rapport à la grandeur approximative d’un attribut quelconque (par exemple, l’attribut de longueur).
Selon Van de Walle et Lovin (2008, p. 296), il importe de faire de la place à l’estimation dans les activités de mesure parce que l’estimation :
- met l’accent sur l’attribut à mesurer et sur la connaissance des procédures (par exemple, pour estimer la longueur du contour d’une figure plane, soit le périmètre, il faut d’abord penser à ce que signifie l’attribut longueur et dans ce cas le périmètre), et aide à visualiser une façon d’utiliser une unité de mesure pour déterminer le périmètre;
- favorise la motivation intrinsèque (par exemple, les élèves veulent vérifier la justesse de leur estimation);
- permet de se familiariser avec les unités de mesure conventionnelles (par exemple, pour estimer le périmètre du gymnase en mètres, il faut des repères qui correspondent à un mètre).
Aux cycles préparatoire et primaire, les élèves effectuent des estimations en utilisant principalement des unités de mesure non conventionnelles. Elles et ils développent l’habileté à estimer en ayant recours à leurs sens (par exemple, comparer la masse de deux objets en les soupesant), à des sources secondaires de renseignements (par exemple, estimer la quantité de nouilles à faire cuire pour un repas en demandant à une ou à un adulte une façon d’établir une portion) ou à leurs connaissances antérieures (par exemple, estimer le temps qu’il leur faudra pour courir 200 mètres en se référant au temps qu’elles et ils mettent pour courir 100 mètres).
Par la suite, les élèves doivent apprendre à utiliser diverses stratégies pour effectuer des estimations dans des situations de plus en plus complexes en utilisant à la fois des unités de mesure non conventionnelles et conventionnelles. Il importe donc que le personnel enseignant planifie des interventions et un enseignement formel axé sur des stratégies d’estimation particulières. Van de Walle et Lovin (2008a, p. 296-297) proposent l’enseignement de quatre stratégies d’estimation. Ces stratégies sont présentées dans le tableau suivant.
|
Stratégie |
Exemple |
|
Développer et utiliser des repères qui représentent des unités de mesure importantes Les élèves qui se sont constitué un répertoire de repères et qui les utilisent régulièrement réussissent à estimer avec plus d'efficacité et d'aisance. L'estimation de la mesure de l'attribut se fait en le comparant à un repère. |
Pour estimer la mesure d'un angle donné, les élèves peuvent utiliser l'angle droit et l'angle plat comme repères. En superposant mentalement l'image de ces angles sur l'angle donné, ils peuvent conclure que sa mesure est beaucoup plus près de 90° que de 180°. Ils estiment alors que la mesure de l'angle donné est d'environ 100°.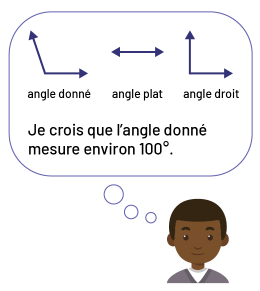 
|
|
Décomposer l'objet en parties Dans certains contextes, il est plus facile d'estimer la grandeur d'un objet en estimant d'abord la grandeur de plus petites sections facilement identifiables. L’estimation de la mesure de l’attribut correspond à la somme de la grandeur de chacune des sections (voir Additivité). |
Pour estimer la hauteur d'un édifice de 12 étages, les élèves peuvent d'abord estimer que la hauteur du premier étage est d'environ 3 m. En supposant que tous les étages ont la même hauteur, ils peuvent alors estimer que l'édifice mesure environ 36 m de hauteur. 
|
|
Utiliser des subdivisons Si l'objet à mesurer ne comporte pas d'éléments qui suggèrent une façon de le décomposer en parties, on peut d'abord le diviser mentalement où concrètement en demis. On peut ensuite diviser une de ces moitiés à nouveau en demis et répéter ainsi le processus jusqu'à l'obtention d'une section dont on peut estimer la mesure. |
Pour estimer l'aire d'une grande couverture, les élèves peuvent la plier en deux à répétition afin d'obtenir une surface de couverture relativement petite. Il leur suffit alors d'estimer l'aire de cette surface, puis de multiplier le résultat par le nombre de ces surfaces ainsi créées. 
Note : Les élèves peuvent établir des liens avec le domaine Algèbre et explorer la relation entre le nombre de plis et le nombre de surfaces créées en pliant, par exemple, une feuille de papier et en notant dans un tableau le nombre de surfaces identiques obtenues après chaque pli. Ils pourraient alors souligner que chaque fois qu'on ajoute un pli, le nombre de surfaces est doublé. 
|
|
Faire des itérations mentalement ou concrètement L'itération désigne l'acte de placer, à plusieurs reprises et d'une manière ordonnée, une même unité de mesure de façon à déterminer la mesure d'un attribut quelconque. L'estimation de la mesure de l'attribut correspond au nombre de fois que l'unité est placée. |
Pour estimer l'aire d'un carton en utilisant un papillon autocollant comme unité de mesure, les élèves peuvent tenter de visualiser le nombre de fois qu'un papillon peut être placé sur le carton sans faire de chevauchements ni laisser d'espaces. 
|
Lorsque les élèves effectuent des activités d’estimation de façon régulière, elles et ils se rendent compte qu’il n’y a pas qu’une seule méthode efficace. Le personnel enseignant doit donc leur proposer de fréquentes activités d’estimation ayant trait aux attributs mesurables. Ces activités s’avèrent pertinentes si les élèves présentent, justifient et expliquent la façon dont elles et ils sont parvenus à leurs résultats. Les explications et les justifications des estimations faites par les élèves permettent au personnel enseignant de connaître et même d’évaluer leur compréhension conceptuelle et des procédures en mesure.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 17-20.
Habileté : mesurer les périmètres de figures planes
La deuxième étape de l’acte de mesurer consiste, selon l’année d’études ou le degré de familiarité des élèves avec l’attribut à mesurer, à choisir une unité de mesure non conventionnelle ou conventionnelle appropriée pour mesurer un attribut quelconque d’un objet.
Pour ce faire, il importe de choisir une unité qui reflète l’attribut à mesurer et qui se prête bien à la situation. De plus, il est généralement préférable d’utiliser une même unité de mesure.
Étapes de l'acte de mesurer
- déterminer l’attribut à mesurer;
- choisir l’unité de mesure;
- déterminer la mesure;
- communiquer le résultat.
Lors des premières explorations d’un attribut d’un objet, il est préférable que le personnel enseignant incite d’abord les élèves à choisir une unité de mesure non conventionnelle, et ce, afin de leur permettre de mieux comprendre le sens de l’attribut et de sa mesure.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 83.
La troisième étape de l’acte de mesurer consiste à déterminer la mesure d’un attribut quelconque d’un objet, c’est-à-dire à donner un ordre de grandeur à l’attribut en le quantifiant en fonction d’une unité de mesure.
Selon la situation, l’élève utilise généralement l’une des stratégies ci-dessous pour déterminer une mesure.
- Comparer et ordonner
- Juxtaposer des unités de mesure
- Utiliser un instrument de mesure
Le choix de la stratégie dépend du contexte, de l’utilisation que l’on veut faire de la mesure, du degré de précision recherché et des instruments de mesure disponibles.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 86.
Pour l’attribut longueur, les élèves doivent visualiser un espace à une dimension, c’est-à-dire une image mentale d’une ligne droite ou d’une courbe. Par exemple, dans une situation où il est question de déterminer le périmètre d’une figure donnée, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de chacun des côtés qui correspond à la longueur de la ficelle placée autour de cette figure.
Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut longueur peut prendre un autre nom, par exemple :
- la hauteur d’une montagne;
- la largeur d’un prisme;
- l’épaisseur d’un gâteau;
- la taille d’une personne;
- la profondeur d’un lac;
- le périmètre d’une boîte.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 21.
Au cycle primaire, il importe que les élèves apprennent à utiliser certains des instruments de mesure usuels tels que ceux énumérés ci-dessous en tenant compte du degré de précision recherché et de l’importance de l’exactitude de la mesure.
Pour mesurer la longueur (hauteur, largeur, périmètre, distance)
- règle graduée en centimètres et en mètres
- mètre
- ruban à mesurer
- roue graduée en centimètres et en mètres
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 93.
Si un périmètre est constitué de lignes droites, ses parties sont mesurées à l’aide d’une règle, puis les mesures sont combinées. C’est une application de la propriété d’additivité.
Un périmètre irrégulier est difficile à mesurer exactement à l’aide d’une règle. Une ficelle permet de reproduire le périmètre de l’objet pour ensuite le mesurer. La mesure de cette ficelle est alors utilisée comme mesure du périmètre. C’est une application de la structure associée aux unités de mesure.
Remarque : En 3e année, les élèves n’utilisent pas de nombres décimaux pour mesurer.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Concepts fondamentaux : additivité et structure associée aux unités de mesure
Additivité
En mesure, l’additivité désigne le concept selon lequel la mesure d’un attribut d’un objet est égale à la somme des mesures de ses parties.
L’élève qui comprend ce concept réalise que, dans la plupart des situations, la longueur d’un objet est égale à la somme de la longueur de ses parties.
L’élève doit aussi comprendre que ce concept ne s’applique pas à l’attribut longueur dans toutes les situations.
Exemple
« Comment les longueurs des guirlandes fabriquées par Ruth et ses amies et amis peuvent-elles les aider à estimer la largeur du tableau de la salle de classe? »
|
Amie et ami |
Longueur de la guirlande |
|
Ruth |
21 cm |
|
Jasmine |
72 cm |
|
Jason |
56 cm |
|
Simon |
68 cm |
(La largeur du tableau est égale à la somme des longueurs des guirlandes.)
Exemple
« André estime et mesure le périmètre du carré initial d’un tangram. En utilisant toutes les mêmes figures, il construit une nouvelle forme. La longueur du périmètre de cette forme est-elle la même que celle du carré? »
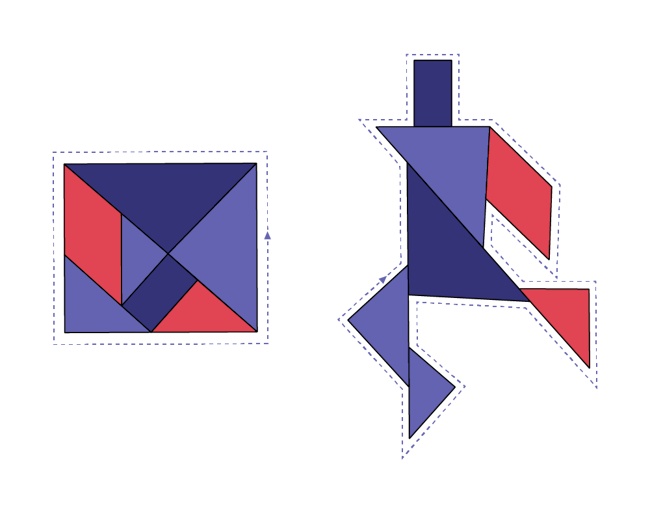
(Non, le périmètre du carré initial est plus petit que la somme des périmètres de ses parties.)
Structure associée aux unités de mesure
Le concept de structure associée aux unités de mesure désigne la façon dont ces unités sont organisées pour déterminer la grandeur d’un espace donné, qu’il soit à une, à deux ou à trois dimensions. Il est lié de près au concept d’itération et est à la base de la stratégie de juxtaposition utilisée pour déterminer une.
L’élève qui comprend ce concept réalise que les unités de mesure de longueur sont juxtaposées dans un espace à une dimension, sans espace ni chevauchement, de façon à recouvrir la distance entre deux extrémités d’un objet.
Exemple
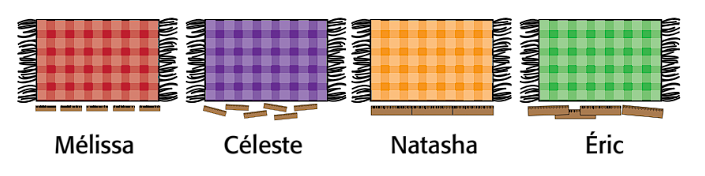
« Quatre élèves ont mesuré la largeur de napperons identiques à l’aide de bâtonnets. Mais ils ont tous des résultats différents. Qui a mesuré avec exactitude? Explique pourquoi. »
Image
Le napperon rouge de Mélissa est mesuré avec 5 petits bâtons qui sont légèrement espacés. Le napperon violet de
Céleste est mesuré avec 6 petits bâtons qui sont légèrement désalignés. Le napperon jaune de Natasha est mesuré avec 3
bâtons plus grands, ils sont parfaitement disposés. Le napperon vert d’Éric est mesuré avec 4 grands bâtons
désalignés.
(Natasha a mesuré avec exactitude car elle a utilisé des bâtonnets identiques et les a placés en ligne droite le long d’un côté du napperon sans laisser d’espace et sans chevauchement.)
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 55-57.
Source : Fiche-attribut Longueur, GEEM, Mat-3e.
Habileté : comparer le périmètre de polygones
On peut explorer cette habileté avec les élèves en leur demandant de créer un polygone qui a un périmètre donné sur un géoplan, sur du papier quadrillé ou avec une ficelle.
Par la suite, demander aux élèves de se lever et d’aller observer et comparer les polygones créés par leurs pairs. Les élèves constateront qu’elles et ils peuvent créer différents polygones ou figures planes ayant le même périmètre ou une même longueur de ficelle.
Relation entre les dimensions d’une figure plane et son périmètre
Alors que les élèves mesurent le contour d’une maison sur un géoplan à l’aide d’une ficelle, le personnel enseignant amène les élèves à découvrir que le périmètre augmente à mesure que la longueur d’un côté augmente. Il peut poser des questions telles que :
- Si les côtés du toit de la maison étaient plus longs, est-ce que j’utiliserais plus de ficelle, moins de ficelle ou la même longueur de ficelle pour déterminer la mesure du contour?
- Si les murs de la maison étaient plus hauts, est-ce que j’utiliserais plus de ficelle, moins de ficelle ou la même longueur de ficelle pour déterminer la mesure du contour?
- Si les côtés du toit étaient plus courts, est-ce que j’utiliserais plus de ficelle, moins de ficelle ou la même longueur de ficelle pour déterminer la mesure du contour?
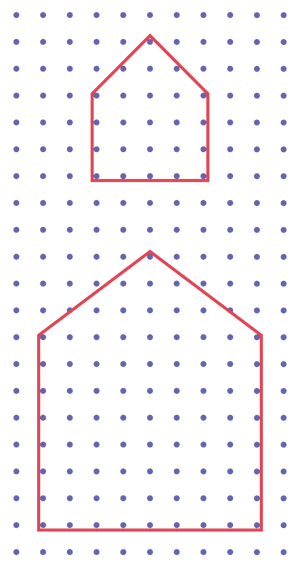
Le personnel enseignant pose des questions pour amener les élèves à découvrir que si l’on augmente la longueur d’un côté, de deux côtés ou de trois côtés d’une figure, son périmètre augmente aussi.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 68.
Habileté : construire des polygones ayant un périmètre donné
Un même périmètre peut prendre des formes très différentes. Une figure plane ayant un périmètre de 20 cm peut être un carré de 5 cm sur 5 cm, un rectangle allongé de 2 cm sur 8 cm ou une ligne courbe fermée.
Pour construire une figure plane ayant un périmètre donné, il faut répartir correctement la longueur autour de la figure plane en surveillant au fur et à mesure la longueur utilisée.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PÉRIMÈTRE (ATTRIBUT LONGUEUR)
Le périmètre d’un objet ou d’une région est la longueur totale de son contour ou de sa périphérie, respectivement. La mesure d’un périmètre est la mesure d’une longueur.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
La longueur est le terme général utilisé pour désigner toute grandeur d’un espace à une dimension que l’on mesure à l’aide d’un objet étalon.
Une longueur peut désigner :
• la grandeur d’un segment, c’est-à-dire la distance entre deux points;
• la distance entre deux droites parallèles ou deux plans parallèles;
• un périmètre;
• une hauteur, une profondeur, une épaisseur, une largeur, une taille (d’une personne).
Note : Pour quelques élèves, ces différents termes associés à la longueur peuvent prêter à confusion. Le terme grandeur utilisé dans la description des attributs longueur, aire et capacité désigne ce qui peut être estimé, évalué ou mesuré.
Exemples
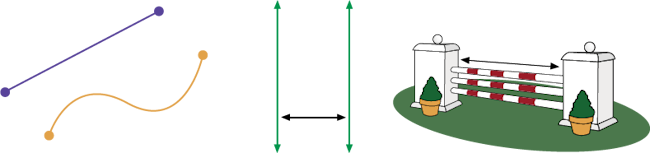Image Deux points reliés par une droite. Deux points reliés par une ligne
courbe. Deux doubles flèches, vertes. Elles sont parallèles. Entre elles est placée une double flèche noire, elle se
place perpendiculairement par rapport aux autres doubles flèches.
Un obstacle pour les chevaux. Une flèche est placée entre les deux socles verticaux.
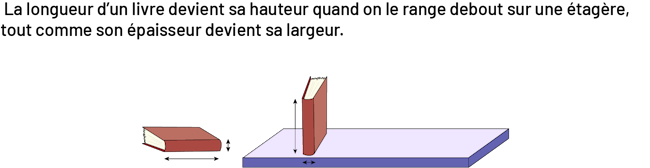Image
Deux livres. Le premier livre est déposé sur le plat de sa couverture. Une flèche montre la longueur du
livre et une autre flèche montre son épaisseur. Le second livre est debout sur une étagère, une flèche montre sa
hauteur et une seconde flèche montre son
épaisseur.
Source : Fiche-attribut Longueur du GEEM Mat-3e, p. 2.
Mesure de la longueur, le diamètre, la circonférence, le périmètre et l’aire.
Description de la vidéo
Description à venir
CONNAISSANCE : POLYGONE
Un polygone est une figure plane formée de plusieurs (poly) côtés. Le polygone est formé d’une ligne brisée et fermée.
Polygones réguliers et irréguliers
Tous les côtés et les angles des polygones réguliers sont congrus. Les côtés et les angles des polygones irréguliers ne sont pas tous congrus.
Ci-dessous, le personnage de gauche est composé de triangles dont certains sont réguliers et d’autres non. Le personnage de droite est composé de pentagones dont certains sont aussi réguliers (visage et mains) et d’autres non.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).