E2.1 Use appropriate units of length to estimate, measure, and compare the perimeters of polygons and curved shapes, and construct polygons with a given perimeter.
Skill: Using Appropriate Units of Length
- The appropriate unit of length depends on the reason for measuring an object. Smaller units of measure provide more precise measurements than larger units. While non-standard units are appropriate for quick, personal measurements, standard units are used when communicating measurements. Non-standard units can vary. Millimetres, centimetres, metres, and kilometres are all standard units of length.
- If different-sized units are used to measure an object, each unit is counted and tracked separately. If different-sized units are used to measure an object, each unit is counted and tracked separately.
- A combination of units might be used (for example, a combination of centimetres and millimetres for a length between 5 centimetres and 6 centimetres).
Examples of different non-standard and standard units
Non-standard units:
- steps
- stride length
- number of paperclips
- number of pencil length
Standard units:
- millimetre (mm)
- centimetre (cm)
- metres (m)
Examples of measuring tools:
- string
- ruler, metre sticks, measuring tapes
- trundle wheels
- grid paper
- manipulatives (for example, geoboards, square tiles, pentominoes, pattern blocks)
Note: In Grade 3, students do not use decimals in their measurements.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Skill: Estimating Length and Perimeter
Perimeter is the total length or distance around an object or region. A perimeter measurement is a length measurement.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Adults, like students, must approximate quantities in a variety of everyday situations; that is, they must estimate (for example, estimate the number of paperclips needed to measure the width of the table). In measurement, estimating is a process based on visual information and prior experience that allows us to make judgments about the approximate magnitude of some attribute (for example, length).
According to Van de Walle and Lovin (2008), it is important to make room for estimation in measurement activities because estimation:
- focuses on the attribute to be measured and knowledge of procedures (for example, to estimate the width of a table using straws, first think about what width (length) means and then visualize a way to use straws as a unit of area;
- promotes intrinsic motivation (for example, students want to check the accuracy of their estimate);
- allows one to become familiar with standard units (for example, to estimate the height of the gym in metres, for one metre are needed).
In Primary and Junior grades, students make estimates using primarily non-standard base units. They develop the skill to estimate using their senses (for example, comparing the mass of two objects by holding them), secondary sources of information (for example, estimating the amount of noodles to cook for a meal by asking an adult for a serving size), or prior knowledge (for example, estimating how long it will take them to run 200 metres by referring to the time it takes them to run 100 metres).
Subsequently, students must learn to use a variety of strategies to make estimates in increasingly complex situations using both non-standard and standard units. It is therefore important for teachers to plan learning experiences and formal instruction focused on specific estimation strategies. Van de Walle and Lovin (2008) suggest teaching four estimation strategies. These strategies are presented in the following table.
|
Strategy |
Example |
|
Develop and Use Benchmarks That Represent Important Units Students who have built up a repertoire of benchmarks and use them regularly are more successful and comfortable estimating. The estimation of the measurement of the attribute is done by comparing it to a benchmark. |
To estimate the measurement of a given angle, students can use the right angle and the flat angle as benchmarks. By mentally superimposing the image of these angles on the given angle, they can conclude that its measure is much closer to 90° than 180°. They then estimate that the measurement of the given angle is approximately 100°.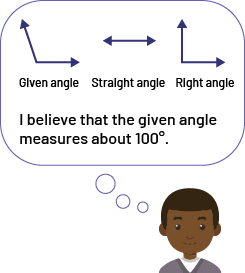 
|
|
Break Down the Object into Parts In some contexts, it is easier to estimate the size of an object by first estimating the size of smaller, easily identifiable parts. The estimate of the attribute’s measurement is the sum of the size of each of the parts (concept of additivity). The estimate of the measurement of the attribute is the sum of the size of each section. (see Additivity). |
To estimate the height of a 12-story building, students can first estimate that the height of the second floor is about 3 m. Assuming that all floors are the same height, they can then estimate that the building is about 36 m high.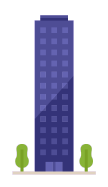 
|
|
Use Subdivisions If the object to be measured has no features that suggest a way to break it down into parts, it can first be divided mentally or physically into halves. One can then divide one of these halves again into halves and repeat the process until a section is obtained whose measurement can be estimated. |
To estimate the area of a large blanket, students can fold it in half repeatedly to create a relatively small blanket area. They can then estimate the area of this surface and multiply the result by the number of such surfaces created. 
Note: Students can make connections to the Algebra strand and explore the relationship between the number of folds and the number of surfaces created by, for example, folding a piece of paper and recording in a chart the number of identical surfaces obtained after each fold. They could then point out that each time a fold is added, the number of surfaces is doubled.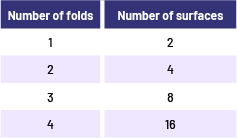 
|
|
Iterate Physically or Mentally Iteration refers to the act of repeatedly placing, in an orderly fashion, the same unit in order to determine the measurement of an attribute. The estimate of the measurement of the attribute is the number of times the unit is placed. |
To estimate the area of a box using a sticky note as a unit of measurement, students can try to visualize the number of times a sticky note can be placed on the cardboard surface without overlapping or leaving gaps. 
|
When students engage in estimation activities on a regular basis, they realize that there is no single effective method. Teachers need to provide frequent estimation activities related to measurable attributes. These activities are most effective if students present, justify, and explain how they arrived at their results. Explanations and justifications of students' estimates allow teachers to learn about and even assess their conceptual and procedural understanding of measurement.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 17-20.
Skill: Measuring the Perimeters of Two-Dimensional Shapes
The second step in the act of measuring is selecting an appropriate non-standard or standard unit to measure an object’s attribute.
To do this, it is important to choose a unit that reflects the attribute to be measured and is appropriate to the situation.
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit;
- determine the measure;
- communicate the result.
When first exploring an attribute of an object, it is best for teachers to encourage students to choose a non-standard unit of measurement first, so that they can focus on the attribute rather than the tool and the more abstract standard units.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 83.
The third step in the act of measuring is to determine the measurement of the attribute for an object quantifying it in terms of a unit.
Depending on the situation, the student typically uses one of the strategies below to determine a measurement.
- Comparing and ordering
- Mentally iterating units
- Using a measuring tool
The choice of strategy depends on the context, the intended use of the measurement, the degree of accuracy sought and the measurement tools available.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 86.
For the attribute of length, students must visualize a one-dimensional space, namely, a mental image of a straight line or curve. For example, in a situation where they are asked to determine the perimeter of a given shape, they must visualize that they are determining the measure of each of the sides that corresponds to the length of the string placed around that shape.
Students should also recognize that in some situations the length attribute may take another name, for example:
- the height of a mountain;
- the width of a prism;
- the thickness of a cake;
- the height of a person;
- the depth of a lake;
- the perimeter of a box.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 21.
In the primary grades, it is important that students learn to use some of the common measuring tools such as those listed below, taking into account the degree of precision required and the importance of accuracy of measurement.
To measure length (height, width, perimeter, distance)
- ruler graduated in centimetres and metres
- metre
- measuring tape
- trundle wheel graduated in centimetres and metres
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3eannée, Mesure, p. 93.
If a perimeter consists of straight lines, its parts are measured with a ruler and then the measurements are combined. This is an application of the additivity property.
Curved perimeters are difficult to measure accurately with a ruler. A “go-between”, like a string, is used to match the perimeter of the object and then measured. This is an application of the transitivity property.
Note: In Grade 3, students do not use decimals in their measurements.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Fundamental Concepts: Additivity and Structure Associated with Units of Measurement
Additivity
In measurement, additivity refers to the concept that the measure of an attribute of an object is equal to the sum of the measures of its parts.
The student who understands this concept realizes that, in most situations, the length of an object is equal to the sum of the length of its parts.
The student must also understand that this concept does not apply to the attribute length in all situations.
Example
”How can the lengths of the garlands Ruth and her friends made help them estimate the width of the classroom chalkboard?“
|
Friend |
Length of the Garland |
|
Ruth |
21 cm |
|
Jasmine |
72 cm |
|
Jason |
56 cm |
|
Simon |
68 cm |
(The width of the chalkboard is equal to the sum of the lengths of the garlands.)
Example
”Andre estimates and measures the perimeter of the original square of a tangram. Using all the same shapes, he constructs a new shape. Is the perimeter length of this shape the same as the perimeter of the square?“
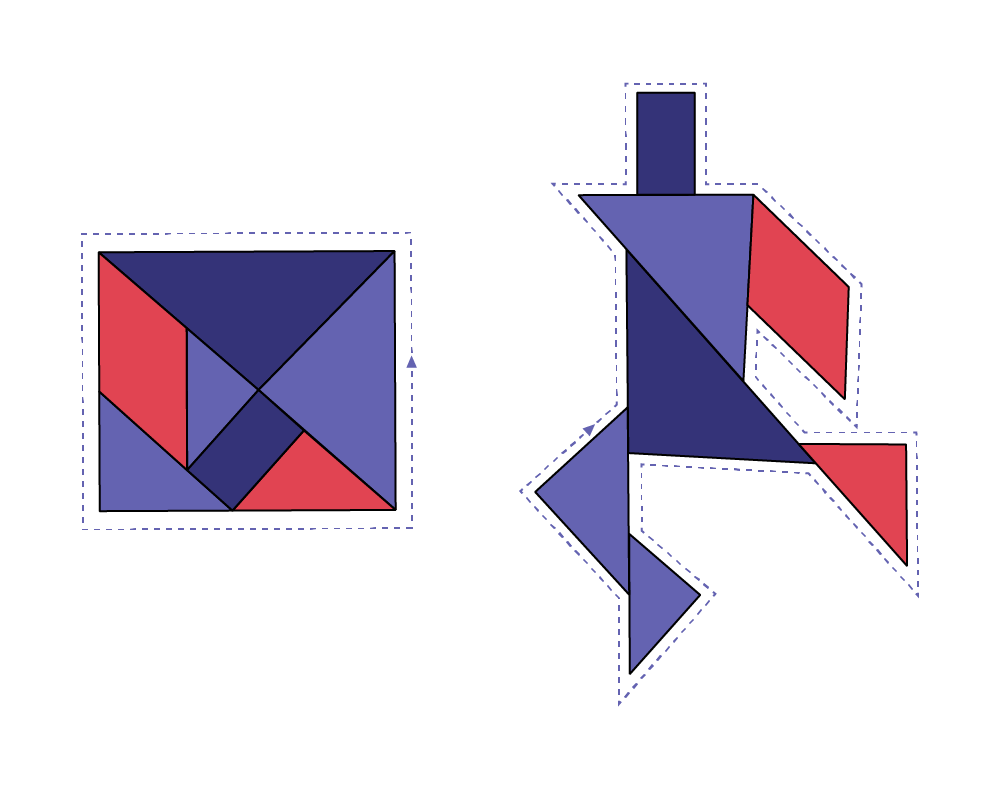
Image A tangram with all shapes forming a square. image The shapes of the tangram form a character. (No, the perimeter of the initial square is different than the sum of the perimeters of its parts.)
Structure Associated with Units of Measurement
The concept of structure associated with units of measurement refers to the way in which these units are organized to determine the magnitude of a given space, whether one-, two-, or three-dimensional. It is closely related to the concept of iteration and is the basis of the juxtaposition strategy used to determine a measurement.
The student who understands this concept realizes that units of length are juxtaposed in a one-dimensional space, without gaps or overlaps, to cover the distance between two ends of an object.
Example
”Four students measured the width of identical placemats with sticks. But they all got different results. Who measured accurately? Explain why.“
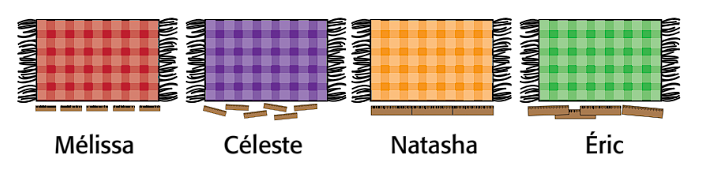Image Melissa's red placemat is measured with 5 small sticks that are slightly spaced. Celeste's
purple placemat is measured with 6 small sticks that are slightly misaligned. Natasha's yellow placemat is measured
with 3 larger sticks, they are perfectly placed. Eric's green placemat is measured with 4 large sticks that are not
aligned.
(Natasha measured accurately because she used identical sticks and placed them in a straight line along one side of the placemat with no gaps and no overlap)
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 55-57 and Fiche attribut Longueur, GEEM, Mat.-3e.
Skill: Comparing the Perimeter of Polygons
This skill can be explored with students by having them create a polygon that has a given perimeter on a geoboard, grid paper, or string.
Students will see that they can create different polygons or two-dimensional shapes with the same perimeter or length of string.
Relationship between the Dimensions of a Two-Dimensional Shape and Its Perimeter
As the students measure the outline of a house on a geoboard using a piece of string, teachers lead the students to discover that the perimeter increases as the length of a side increases. They may ask questions such as:
- If the sides of the house roof were longer, would I use more string, less string, or the same length of string to determine the outline measurement?
- If the walls of the house were higher, would I use more string, less string, or the same length of string to determine the outline measurement?
- If the sides of the roof were shorter, would I use more string, less string, or the same length of string to determine the outline measurement?
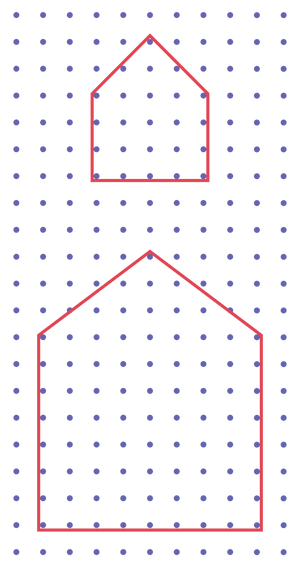
Teachers ask questions to lead students to discover that if you increase the length of one side, two sides, or three sides of a shape, its perimeter also increases.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 68.
Skill: Building Polygons with a Given Perimeter
The same perimeter can take many different shapes. A two-dimensional shape with a perimeter of 20 cm can be a square of 5 cm by 5 cm, an elongated rectangle of 2 cm by 8 cm or a closed curved line.
To construct a two-dimensional shape with a given perimeter, you must correctly distribute the length around the two-dimensional shape by monitoring the length used as you go.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Perimeter (Attribute - Length)
The perimeter of an object or region is the total length of its outline. The measure of a perimeter is a measure of a length.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Length is a measure in a one-dimensional space.
A length can refer to:
• the size of a segment, i.e. the distance between two points;
• the distance between two parallel lines or two parallel planes;
• a perimeter;
• a height, a depth, a thickness, a width, a height (of a person).
Note: For some students, these different terms associated with length may be confusing.
Examples
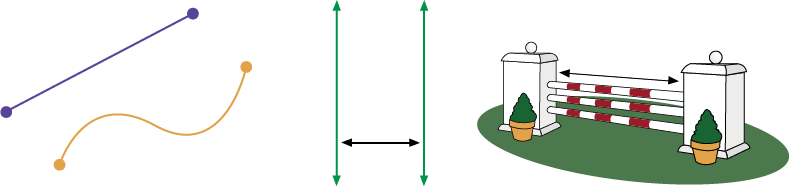Image Two points connected by a straight line. Two points connected by a curved line. Two double
arrows, green. They are parallel. Between them is placed a black double arrow, it is perpendicular to the
other double arrows.
An obstacle for the horses. An arrow is placed between the two vertical bases.
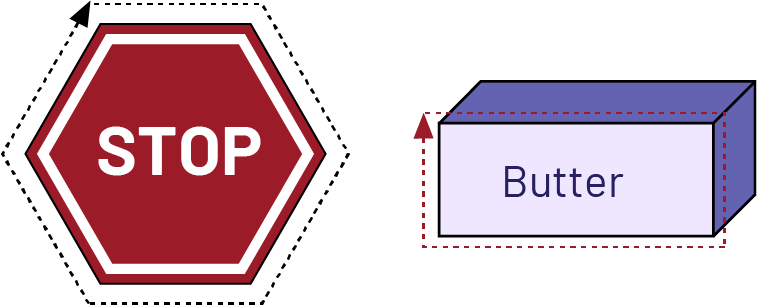
Image A "stop" sign. A dotted line outlines the sign. A rectangular shape with the word butter written on one side. A dotted line outlines one side of the prism.
The perimeter is the length around a two-dimensional shape or three-dimensional object.
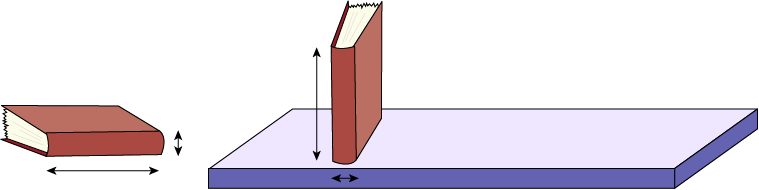
Image Two books. The first book is placed on its cover. An arrow shows the length of the book and another arrow shows its thickness.
The second book is standing on a shelf, one arrow shows its height and a second arrow shows its thickness.
The length of a book becomes its height when stored upright on a shelf, just as its thickness becomes its width.
Source: translated from Fiche attribut Longueur, GEEM Mat-3e, p. 2.
Knowledge: Polygon
A polygon is an enclosed shape formed from several (poly) sides.
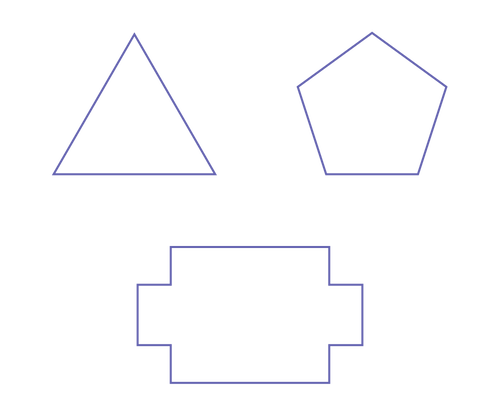
Regular and Irregular Polygons
All sides and angles of regular polygons are congruent. Not all sides and angles of irregular polygons are congruent.
Below, the character on the left is made of triangles, some of which are regular and others not. The character on the right is made of pentagons, some of which are also regular (face and hands) and others not.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).