E2.2 Expliquer la relation entre les millimètres, les centimètres, les mètres et les kilomètres comme unités de mesure de longueur du système métrique, et utiliser des repères représentant ces unités pour estimer des longueurs.
HABILETÉ : EXPLIQUER LA RELATION ENTRE MILLIMÈTRES, CENTIMÈTRES, MÈTRES ET KILOMÈTRES
L’analyse de relations, qui est tout aussi importante dans le domaine Sens de l’espace que dans celui de l’Algèbre, mène les élèves à formuler une généralisation. Pour ce faire, elles et ils peuvent suivre un processus informel comme celui illustré ci-dessous.
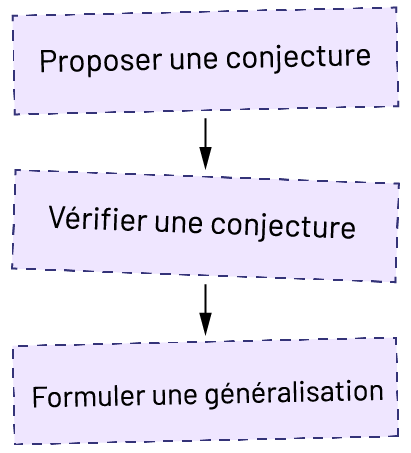
L’analyse des relations permet aux élèves de développer leur sens de la mesure, ainsi que leur compréhension des unités de mesure conventionnelles.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 60.
Le millimètre, le centimètre, le mètre et le kilomètre sont des unités de longueur conventionnelles du système international d’unités (SI), communément appelé système métrique. Le mètre est l’unité de longueur conventionnelle ou de base du SI ou du système métrique.
- Un mètre équivaut à 100 centimètres ou à 1 000 millimètres.
- Un kilomètre équivaut à 1 000 mètres.
La mesure d’une longueur est toujours approximative. Plus l’unité utilisée est petite, plus la mesure sera exacte.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Relation inverse
La grandeur de l’unité a une incidence sur le nombre d’unités obtenu. Ainsi, il existe une relation inverse entre la grandeur de l’unité et le nombre d’unités nécessaire pour mesurer un attribut. Plus l’unité de mesure utilisée est petite, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est grand. Plus l’unité de mesure utilisée est grande, plus le nombre d’unités requis pour déterminer la mesure est petit.
Peu importe la grandeur de l’unité utilisée pour mesurer la longueur d’un objet, la longueur demeure la même. Seul le nombre d’unités change. Il s’agit du concept de conservation.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Les diverses unités de mesure conventionnelles associées à l’attribut longueur font partie d’un système décimal d’unités. On utilise ce fait mathématique pour établir des relations d’équivalence entre ces unités. Par exemple, explorer des activités de mesure de longueur qui amènent les élèves à comprendre la relation inverse entre le millimètre et le centimètre, entre le centimètre et le mètre, et entre le mètre et le kilomètre. Ces activités les mèneront à décrire la généralisation qu’il y a toujours :
- 10 mm dans un centimètre;
- 100 cm dans un mètre;
- 1000 m dans un kilomètre.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 64-65.
HABILETÉ : UTILISER DES REPÈRES POUR ESTIMER DES LONGUEURS (MM, CM, M, KM)
Lorsqu’on dispose des repères familiers pour les millimètres, les centimètres, les mètres et les kilomètres, il est plus facile d’estimer la longueur des objets.
Exemples de repères
- Kilomètre : distance entre la maison et l’école
- Mètre : longueur de l’envergure des bras
- Centimètre : largeur d’un doigt
- Millimètre : épaisseur d’une pièce de 10 cents
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Développer le sens de la mesure chez les élèves requiert de développer des habiletés très importantes telles que s’approprier des repères, estimer, visualiser, résoudre des situations-problèmes, raisonner et communiquer.
En mesure, les repères sont des images mentales qui représentent des grandeurs ou des unités de mesure non conventionnelles ou conventionnelles selon des schèmes de référence donnés ou personnels.
Image
Dans un encadré on peut lire : « À quoi penses-tu lorsque tu t’imagines une distance de 400 mètres ? » (Parenthèse
ouvrante) C’est un tour de la piste de course de l’école secondaire voisine (parenthèse fermante)
Si les repères peuvent varier d’une personne à l’autre, tous revêtent une signification particulière pour celle ou celui qui les utilisent pour estimer une mesure quelconque.
Progression en matière d’utilisation de repères
Au fil de leurs explorations en mesure, les élèves apprennent à faire une utilisation de plus en plus complexe et abstraite des repères. Selon Joram (2003, p. 65 et 66), cette progression est caractérisée par trois niveaux, et le personnel enseignant doit aider les élèves à cheminer au travers de chacun d’eux.
Au premier niveau, comme illustré dans l’exemple ci-dessous, les élèves se servent d’objets ou de matériel de manipulation autant comme repères que comme unités de mesure non conventionnelles. Cette utilisation de repères concrets est essentielle à la construction d’un repère au sens pur. Elle convient bien aux élèves du cycle primaire, car leur capacité à construire et à conserver des images mentales exactes est en développement. À ce niveau, les élèves peuvent aussi utiliser les repères concrets pour représenter des unités de mesure conventionnelles.
Exemple
La largeur de mon auriculaire égale presque la longueur d’un centimètre.
Si n’importe quel objet peut servir de repère concret, le personnel enseignant doit s’assurer que son utilisation est appropriée. Le tableau ci-dessous présente quelques repères concrets, leur avantage ainsi que certains éléments à prendre en considération avant d’en proposer ou d’en accepter l’utilisation.
|
Repères concrets |
Avantage |
Considération |
|
Parties du corps (par exemple, main, pied)
|
Elles sont à la dispositions des élèves en tout temps. |
Elles ne constituent pas toujours des repères concrets idéaux en raison de la variations de mesure résultant de la croissance de élèves. |
|
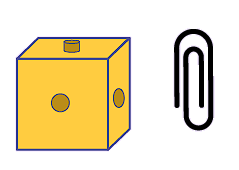
Matériel de manipulation (par exemple, cube emboîtable, trombone)
|
Il s'obtient facilement en grande quantité et à un coût raisonnable. |
Il ne devrait pas être le seul repère concret utilisé. Puisqu'il est couramment utilisé pour mesurer plusieurs attributs (par exemple, longueur, aire, capacité), il est important d'indiquer la partie de l'objet qui est utilisée comme repère (par exemple, la longueur de la base d'un cube). Il ne renvoie pas à un schème personnel ou à une expérience significative. |
|
Objets personnels (par exemple, figurine, peluche, petite voiture, espadrille)
|
Ils sont significatifs pour les élèves. |
Ils augmentent la possibilité que les élèves les utilisent couramment et qu'elles et ils établissent les liens avec les unités de mesure conventionnelles. Ils favorisent la création d'un ensemble d'images mentales qui serviront de repères personnels. |
Au deuxième niveau, les élèves remplacent les repères concrets par des images mentales qu’elles et ils utilisent comme référence pour estimer une mesure (par exemple, l’utilisation de l’image mentale de la largeur de l’auriculaire pour estimer une longueur en centimètres).
Exemple
Image Le visage d’une élève, une bulle de parole lui est associée. On peut y
lire : « JE crois que l’épaisseur de mon livre est d’environ 4 centimètres, car elle correspond à peu près à 4 fois la
largeur de mon auriculaire » . Une bulle de pensées est associée à l’élève, on peut y voir : « le livre et une double
flèche à l’épaisseur, 4 centimètres.
À ce niveau, les élèves peuvent percevoir chaque unité comme un objet particulier, sans en comprendre pleinement le sens selon un système de mesure. Par exemple, l’élève perçoit que l’épaisseur du livre est de 4 centimètres, mais ne comprend pas que cela équivaut à 0,04 mètre. L’utilisation répétée d’images mentales de repères concrets favorise la compréhension du sens et de la grandeur des diverses unités de mesure conventionnelles et de leurs multiples (par exemple, centimètre, mètre).
Au troisième niveau, les élèves intègrent les repères à un système de mesure, ce qui leur permet notamment d’établir des relations entre diverses unités de mesure conventionnelles d’un même attribut (par exemple, centimètre, mètre) et de donner un sens aux stratégies de conversion entre ces unités.
Exemple
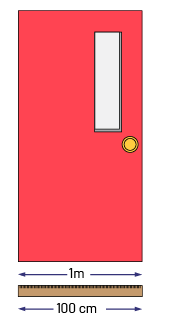
Conception de repères
Puisque les repères sont essentiellement des images mentales, leur conception est intimement liée à l’habileté à visualiser. Les élèves n’ont généralement pas trop de difficulté à concevoir des repères appropriés pour l’attribut de longueur (par exemple, image de la longueur d’un côté d’un petit cube emboîtable pour représenter 1 centimètre, de la longueur d’une règle pour tableau pour représenter 1 mètre).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 12-15.
CONNAISSANCE : SYSTÈME MÉTRIQUE
Le monde scientifique a universellement recours au système métrique parce que ce système utilise des préfixes normalisés qui facilitent la compréhension des mesures et des conversions.
Bien que le Canada ait adopté officiellement en 1970 le système international d’unités (SI), communément appelé système métrique, la Loi sur les poids et mesures a été modifiée en 1985 pour permettre à la population canadienne d’utiliser les unités impériales (ou « unités canadiennes » aux termes de la Loi) en plus des unités métriques. Outre les unités métriques, on compte parmi les unités de longueur conventionnelles le pouce, le pied, la verge et le mille. La longueur se mesure de la même façon avec des unités canadiennes, autrefois appelées impériales, qu’avec des unités métriques ou non conventionnelles. Seuls les unités et les instruments de mesure changent.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.