E2.2 Explain the relationships between millimetres, centimetres, metres, and kilometres as metric units of length, and use benchmarks for these units to estimate lengths.
Skill: Explaining the Relationship Between Millimetres, Centimetres, Metres and Kilometres
The analysis of relationships, which is just as important in Spatial Sense strand as it is in Algebra, leads students to formulate a generalization. To do this, they can follow an informal process like the one illustrated below.
Image Three word labels in a row and with an arrow between them. "Propose a conjecture", "Check a conjecture", "Formulate a generalization".
Analyzing relationships allows students to develop their sense of measurement, as well as their understanding of standard units of measurement.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 60.
Millimetres, centimetres, metres, and kilometres are standard metric units of length. The metre is the metric standard or base unit of length.
- 1 metre is equal to 100 centimetres or 1 000 millimetres.
- 1 000 metres is equal to 1 kilometre.
The measurement of a length is always approximate; the smaller the unit used, the more accurate the measurement.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Inverse Relationship
The size of the unit affects the number of units obtained. Thus, there is an inverse relationship between the size of the unit and the number of units required to measure an attribute. The smaller the unit of measure used, the greater the number of units required to determine the measure of the attribute. The larger the unit of measure used, the smaller the number of units required to determine the measure.
No matter what size unit is used to measure the length of an object, the length remains the same. Only the number of units changes. This is the concept of conservation.
Source: The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.
The metric standard units associated with the attribute length are derived from a system of units that are related by factors of powers of ten. This mathematical fact is used to establish equivalence relationships between these units. For example, explore length measurement activities that lead students to understand the inverse relationship between millimetres and centimetres, centimetres and metres, and metres and kilometres. These activities will lead them to formulate the generalization that there is always:
- 10 mm in a centimetre;
- 100 cm in one metre;
- 1000 m in one kilometre.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 64-65.
Skill: Using Benchmarks to Estimate Lengths (mm, cm, m, km)
When you have familiar benchmarks for millimetres, centimetres, metres and kilometres, it is easier to estimate the length of objects.
Examples of Benchmarks
- Kilometre: distance between home and school
- Metre: length of the armspan
- Centimetre: width of a finger
- Millimetre: thickness of a 10 cent coin
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Developing a sense of measurement requires the development of very important skills such as benchmarking, estimating, visualizing, problem solving, reasoning, and communicating.
In measurement, benchmarks are mental images that represent non-standard or standard quantities or units according to a given or personal referent.
Image In a box it says: "What do you think of when you imagine a distance of 400 meters?" ( Open parenthesis) It's a lap around the high school track next door ( Close parenthesis).
While the benchmarks may vary from person to person, all of them have a special meaning to the person using them to estimate some measure.
Progression in the Use of Benchmarks
As students explore in measurement, they learn to make increasingly complex and abstract use of benchmarks. According to Joram (2003, pp. 65-66), this progression is characterized by three levels, and teachers need to help students move through each level.
At the first level, as illustrated in the example below, students use objects or manipulatives as both benchmarks and non-standard units of measurement. This use of concrete benchmarks is essential to the construction of a pure benchmark. It is well suited to students in the primary grades, as their ability to construct and maintain accurate mental images is developing. At this level, students can also use concrete benchmarks to represent standard units of measurement.
Example
The width of my little finger is almost equal to the length of a centimetre.
While any object can be used as a concrete benchmark, teachers need to ensure that it is used appropriately. The table below outlines some concrete markers, their benefits, and some things to consider before proposing or accepting their use.
|
Concrete Benchmarks |
Benefit |
Consideration |
|
Body parts (for example, hand, foot)
|
They are available to students at all times. |
They are not always ideal concrete benchmarks because of the variation in measurement resulting from the growth of students. |
|
Manipulatives (for example, linking cubes, paperclips)
|
It is easily available in large quantities and at a reasonable cost. |
It should not be the only concrete benchmark used. Since it is commonly used to measure several attributes (for example, length, area, capacity), it is important to indicate which part of the object is being used as a benchmark (for example, the length of the base of a cube). It does not refer to a personal pattern or a significant experience. |
|
Personal items (for example, figurine, stuffed animal, toy car, sneaker)
|
They are meaningful to students. |
They increase the likelihood that students will use them comfortably and make connections to standard units of measurement. They encourage the creation of a set of mental images that will serve as personal reference points. |
At the second level, students replace concrete benchmarks with mental images that they use as a referent to estimate a measurement (for example, using the mental image of the width of the little finger to estimate a length in centimetres).
Example
Image The face of a student, a speech bubble is associated with it. It says: "I think the thickness of my book is about 4 centimeters, because it is about 4 times the width of my little finger. A thought bubble is associated with the student, it reads: "the book and a double arrow at the thickness, 4 centimeters.
At this level, students may perceive each unit as a particular object, without fully understanding its meaning according to a measurement system. For example, the student perceives that the thickness of the book is 4 centimetres, but does not understand that this is equivalent to .04 metres. Repeated use of mental images of concrete benchmarks promotes understanding of the meaning and magnitude of various standard units of measurement and their multiples (for example, centimetre, metre).
At the third level, students integrate benchmarks into a measurement system, including establishing relationships among various standard units of the same attribute (for example, centimetre, metre) and making sense of conversion strategies among these units.
Example
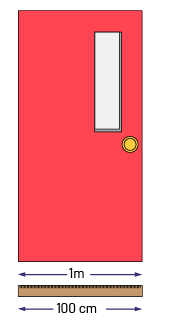Image A red door labeled "one meter equals 100 centimeters. A measuring tape, a double arrow that joins the two ends, one meter, a second double arrow equals 100 centimetres.
Benchmark Development
Since reference points are essentially mental images, their development is intimately related to the ability to visualize. Students generally do not have too much difficulty developing appropriate benchmarks for length (for example, they can imagine the length of one side of a small interlocking cube to represent 1 centimetre, or the length of a metre stick to represent 1 metre).
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 12-15.
Knowledge: Metric System
The scientific world universally uses the metric system because it uses standardized prefixes that make measurements and conversions easier to understand.
Canada officially adopted the metric system in 1970, through the Weights and Measures Act. This act was amended in 1985 to allow Canadians to use a combination of metric and imperial units (called “Canadian” units in the Weights and Measures Act). In addition to metric units, other common standard units of length are inches, feet, yards, and miles. The process for measuring length with imperial units is the same as for using metric and non-standard units. Only the length of the unit and the measuring tools differ.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.