E2.7 Comparer les aires de figures planes en les faisant correspondre, en les superposant ou en les décomposant et les recomposant, et démontrer que différentes figures peuvent avoir la même aire.
HABILETÉ : COMPARER LES AIRES DE FIGURES PLANES ET DÉMONTRER QUE DIFFÉRENTES FIGURES PLANES PEUVENT AVOIR LA MÊME AIRE
Au cycle primaire, des concepts fondamentaux sont essentiels au développement de la compréhension des attributs mesurables. La conservation est un des concepts fondamentaux.
« Tant que les élèves n’ont pas appris à “conserver”, comme le dit Piaget, leurs comparaisons peuvent être déformées par un facteur conceptuel ou un autre. »
(Copley, 2000, p. 132, traduction libre)
En mesure, la conservation désigne le concept selon lequel la mesure d’un attribut, en unités non conventionnelles ou conventionnelles, demeure la même que l’objet soit déplacé, transformé ou décomposé.
Il est important que le personnel enseignant demande régulièrement aux élèves de transformer, de déplacer ou de décomposer un objet et d’en comparer la mesure d’attributs quelconques, en unités non conventionnelles ou conventionnelles, avant et après la transformation.
Elles et ils pourront ainsi se questionner, échanger leurs idées et comprendre les circonstances dans lesquelles le concept de conservation s’applique.
Exemple du concept de conservation de l’aire
L’aire des figures 1 et 2 est la même que l’aire du carré, car les trois figures sont construites à partir des sept mêmes pièces d’un jeu de tangram.
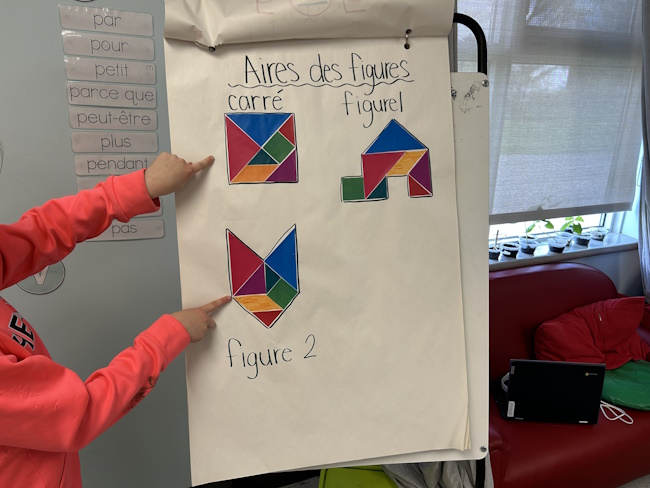
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 53.
L’élève qui comprend ce concept réalise que l’aire d’une surface demeure la même, que la surface soit déplacée, transformée ou décomposée.
Exemple
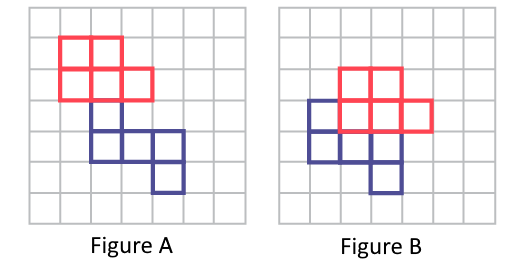
« Luc choisit deux pentaminos et les assemble pour créer une figure. Il trace cette figure sur du papier quadrillé et colore les carrés qui font partie de cette figure. Il crée une autre figure avec les mêmes pentaminos. Que remarques-tu au sujet de l’aire des deux figures de Luc? »
Image
Sur deux espaces quadrillés, deux pentaminos sont utilisés pour faire un dessin. Les deux formes de pentaminos sont
déterminées par les couleurs rouge et bleu. Dans la première grille, la forme ressemble à une fleur. Dans la seconde
grille, les pentaminos sont imbriqués.
L’aire de chaque figure est identique; chacune occupe le même nombre de carrés, mais ils sont disposés différemment. L’aire n’a pas augmenté ou diminué; l’aire représente toujours l’aire de la surface des deux pentaminos choisis.
Additivité
Un autre concept fondamental à développer chez les élèves est celui de l’additivité. L’élève qui comprend ce concept réalise que l’aire d’une figure est égale à la somme de l’aire de chacune de ses parties.
Exemple
« Sur un géoplan, un élève crée deux rectangles contigus. Il estime et mesure l’aire de chaque rectangle. Avec un élastique de couleur différente, il réunit les deux rectangles dans une même figure. Compare l’aire de cette nouvelle figure avec celle des figures initiales. »
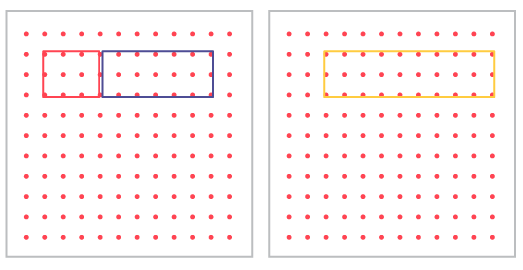Image Sur un géoplan, un élastique rouge représente un carré. À sa suite, un
élastique bleu représente un rectangle qui a le double de la surface que le carré. Sur un deuxième géoplan, un
élastique vert représente la surface totale du carré et du rectangle.
L’aire de la nouvelle figure est égale à la somme de l’aire des deux rectangles réunis. L’aire de l’exemple ci-dessus est : 6 unités carrées + 12 unités carrées = 18 unités carrées.
Source : Fiche de la maternelle à la 3e année Attribut aire.
CONNAISSANCE : ATTRIBUT AIRE
L’aire est le nombre servant à mesurer la surface d’une région plane ou l’espace qu’elle contient.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Pour l’attribut aire, les élèves doivent visualiser un espace à deux dimensions, c’est-à-dire se faire une image mentale d’une surface plane ou courbe. Par exemple, dans une situation où il est question de calculer l’aire d’un rectangle donné, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de l’espace occupé par la surface de cette figure. Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut aire peut prendre un autre nom, par exemple :
- l’étendue d’un terrain;
- la superficie d’une ville.
L’aire désigne la grandeur d’une surface ou d’un espace à deux dimensions.
Exemple 1
Je détermine l’aire de la face du haut de la boîte en le recouvrant de papillons adhésifs.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 46.
Exemple 2
L’élève démontre sa compréhension de l’aire en recouvrant la surface de mosaïques géométriques.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 126.
J’ai utilisé 4 losanges, 4 triangles verts et 1 hexagone jaune pour couvrir le cerf-volant. Les formes ne se chevauchent pas.
Le personnel enseignant pose des questions telles que :
- Que remarques-tu?
- Quelle est l’aire du carré? Est-ce efficace comme stratégie pour mesurer l’aire? Quels changements pourrais-tu apporter?
- Peux-tu comparer l’aire de ton carré avec l’aire d’un carré d’une autre équipe? Que remarques-tu?
Le questionnement ouvert du personnel enseignant permet à l’élève d’approfondir sa compréhension du concept de l’aire. L’élève doit comprendre que, pour mesurer efficacement l’aire d’une figure plane, les unités de mesure doivent être placées sans espacement et sans chevauchement. Lorsque la figure plane est complètement recouverte de différentes unités de mesure non conventionnelles, une conversion est nécessaire pour communiquer plus facilement une mesure. Par exemple, dans l’image ci-dessus, l’élève peut remarquer que l’hexagone est formé de six triangles et que chacun des losanges contient deux triangles. L’aire pourrait donc être de 18 triangles.
L’élève modifie les mosaïques géométriques utilisées pour mesurer l’aire du carré en utilisant seulement des triangles verts et en s’assurant de ne laisser ni espace ni chevauchement entre les triangles.