E2.7 Compare the areas of two-dimensional shapes by matching, covering, or decomposing and recomposing the shapes, and demonstrate that different shapes can have the same area.
Skill: Comparing the Areas of Two-Dimensional Shapes and Demonstrating That Different Two-Dimensional Shapes Can Have the Same Area
In the primary grades, fundamental concepts are essential to the development of an understanding of measurable attributes. Conservation is one of the fundamental concepts.
In measurement, conservation refers to the concept that the measurement of an attribute, in either standard and non-standard units, remains the same whether the object is moved, transformed, or decomposed.
It is important that teachers regularly ask students to transform, move, or decompose an object and compare the measurement of any attributes, in standard and non-standard units, before and after the transformation.
They will be able to question each other, exchange ideas and understand the circumstances in which the concept of conservation applies.
Example of the Conservation of Area
The area of shapes 1 and 2 is the same as the area of the square, because all three shapes are constructed from the same seven pieces of a tangram set.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 53.
The student who understands this concept realizes that the area of a surface remains the same whether the surface is moved, transformed, or decomposed.
Example
”Luke chooses two pentominoes and puts them together to create a shape. He draws this shape on graph paper and colors the squares that are part of this shape. He creates another shape with the same pentominoes. What do you notice about the area of Luke's two shapes?“
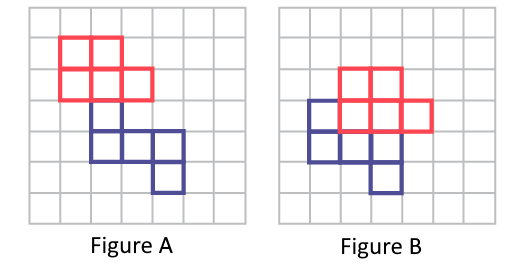
Image On two grid spaces, two pentominoes are used to make a shape. The two pentomino shapes are determined by the colors red and blue. In the first grid, the shape looks like a flower. In the second grid, the pentominoes are interlocked.
The area of each shape is identical; each occupies the same number of squares, but they are arranged differently. The area has not increased or decreased; the area still represents the area of the two selected pentominoes.
Additivity Example
Another fundamental concept for students to develop is that of additivity. Students who understand this concept realize that the area of a shape is equal to the sum of the area of each of its parts.
Example
”On a geoboard, a student creates two adjacent rectangles. They estimate and measure the area of each rectangle. Using a different colored rubber band, they join the two rectangles into a single shape. Compare the area of this new shape with the area of the original shapes.“
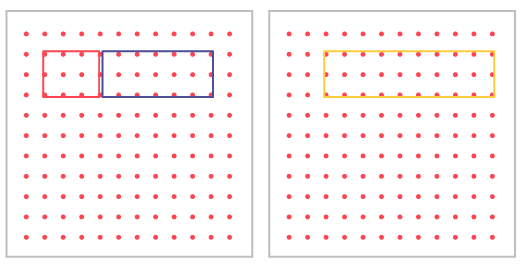Image On a geoplan, a red rubber band is a square. Next, a blue rubber band shows a rectangle that has
twice the area of the square. On a second geoplan, a green rubber band shows the total area of the square and the
rectangle.
The area of the new shape is equal to the sum of the area of the two rectangles combined. The area of the above example is: 6 square units + 12 square units = 18 square units.
Source: translated from Fiche de la maternelle à la 3e année Attribut aire.
Knowledge: Attribute - Area
Area is the measure of the amount of space inside a two-dimensional shape.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Students form a mental image of a flat or curved surface to find its area. For example, in a situation where the area of a given rectangle is to be determined, students need to visualize that they are finding the measure of the space occupied within the rectangle. Students should also recognize real-life situations that involves this attribute, for example:
- the size of a piece of land;
- the area of a city.
Example 1
I determine the area of the top face of the box by covering it with sticky notes.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 46.
Example 2
Students will demonstrate their understanding of area by covering the surface with pattern blocks.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 126.
I used 4 rhombuses, 4 green triangles and 1 yellow hexagon to cover the kite. The shapes do not overlap.
Teachers ask questions such as:
- What do you notice?
- What is the area of the kite? Is this an effective strategy for measuring area? What changes could you make?
- Can you compare the area of your kite with the area of another team's kite? What do you notice?
Open-ended questioning by the teacher supports students to deepen their understanding of the concept of area. Students need to understand that in order to effectively measure the area of a two-dimensional shape, the units must be placed without spacing and overlap. When the two-dimensional shape is completely covered with different non-standard units, a conversion is necessary to determine one unit of measure. For example, in the image above, the student may notice that the hexagon can be made with six triangles and each of the rhombuses can be made with two triangles. Therefore, the area is equivalent to18 triangles.
To support students to grasp this concept, ask them to measure the area of the kite using only green triangles and making sure to leave no gaps or overlaps between the triangles. Encourage them to think about how they might swap the pieces they already have for green triangles.