E2.8 Utiliser des unités de mesure non conventionnelles appropriées pour mesurer l’aire et expliquer l’incidence du chevauchement et des espaces entre les unités sur l’exactitude de la mesure.
HABILETÉ : MESURER L’AIRE EN UTILISANT DES UNITÉS DE MESURE NON CONVENTIONNELLES ET EXPLIQUER L’INCIDENCE DU CHEVAUCHEMENT ET DES ESPACES SUR L’EXACTITUDE DE LA MESURE
Selon Van de Walle et Lovin (2008, p. 296), il importe de faire de la place à l’estimation dans les activités de mesure parce que l’estimation met l’accent sur l’attribut à mesurer et sur la connaissance des procédures. Par exemple, pour estimer l’aire de la surface de la couverture d’un livre à l’aide de cartes à jouer ou de papillons adhésifs, il faut d’abord penser à ce que signifie l’aire et, ensuite, visualiser une façon d’utiliser les cartes ou les papillons adhésifs comme unité de mesure d’aire.
Au cycle primaire, des concepts fondamentaux sont essentiels au développement de la compréhension des attributs mesurables.
Structure associée aux unités de mesure
« Pour chacun des trois attributs longueur, aire et volume, une structure est associée aux unités de mesure en fonction de la façon dont les unités recouvrent les objets à mesurer, et il y a des liens étroits entre ces structures. »
(Curry, Mitchelmore et Outhred, 2006, p. 377, traduction libre)
Le concept de structure associée aux unités de mesure désigne la façon dont ces unités sont organisées pour déterminer la grandeur d’un espace donné, qu’il soit à une, à deux ou à trois dimensions. Il est lié de près au concept d’itération et est à la base de la stratégie de juxtaposition utilisée pour déterminer une mesure. Les exemples ci-dessous précisent le sens de ce concept à l’aide de situations concrètes.
Exemple
Pour déterminer l’aire d’un rectangle, les unités de mesure doivent être juxtaposées dans un espace à deux dimensions, sans espace ni chevauchement, de façon à recouvrir le rectangle selon une disposition rectangulaire constituée de colonnes et de rangées.
Le personnel enseignant peut vérifier si les élèves ont bien compris ce concept en leur demandant, par exemple, d’estimer, puis de déterminer l’aire d’un rectangle dans lequel une rangée et une colonne de carrés sont dessinées.
Les élèves qui n’ont pas compris la structure associée aux unités d’aire ne visualisent pas que les unités sont organisées de façon ordonnée en colonnes et en rangées. Elles et ils ont tendance à recouvrir la surface du rectangle de façon plus ou moins aléatoire à l’aide d’unités de grandeur variable et ont ensuite de la difficulté à dénombrer ces unités.
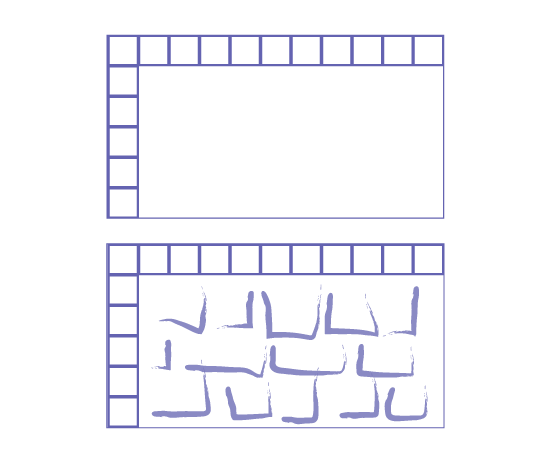Image Un espace rectangulaire est occupé par une série de carrés qui longe la longueur et la largeur.
Un espace rectangulaire est occupé par une série de carrés qui longe la longueur et la largeur. Des tracés aléatoires
occupent le reste du plan.
En revanche, les élèves qui ont compris ce concept peuvent terminer la disposition rectangulaire en juxtaposant des unités carrées en colonnes et en rangées sur toute la surface du rectangle. Elle et ils reconnaissent :
- que chaque colonne a le même nombre d’unités carrées (par exemple, 5) et que ce nombre correspond à la mesure de la hauteur du rectangle;
- que chaque rangée a le même nombre d’unités carrées (par exemple, 9) et que ce nombre correspond à la mesure de la base du rectangle.
Cette compréhension leur permet d’établir un lien entre la mesure de la base d’un rectangle, sa hauteur et son aire, d’expliquer la raison pour laquelle la mesure est exprimée en unités carrées et, éventuellement au cycle moyen, de donner un sens à la formule usuelle du calcul de l’aire d’un rectangle. Il est donc important d’amorcer la compréhension de ce concept dès le cycle primaire.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 17, 57, 58.
Concept d’itération
L’élève qui comprend ce concept réalise qu’il est possible de déterminer l’aire d’une surface en lui superposant, à plusieurs reprises et de manière ordonnée, un seul objet étalon ou une seule unité de mesure d’aire conventionnelle ou non conventionnelle.
Exemple
Combien de carrés à la guimauve peut-on faire en utilisant un moule si chaque carré couvre l’espace d’un papillon adhésif?
Il suffit de placer successivement un papillon adhésif, sans espace ni superposition, sur toute la surface du moule. On peut alors déterminer le nombre de fois qu’un papillon adhésif a été placé pour obtenir l’aire de la surface du moule et le nombre de carrés à la guimauve.
Source : Fiche attribut Aire, Mat-3e.
Stratégie de juxtaposition
Juxtaposer des unités de mesure consiste à placer soigneusement un certain nombre d’objets étalons comme unités de mesure de façon à recouvrir une surface pour déterminer son aire.
Exemple 1
Un élève détermine l’aire de la surface du drapeau en plaçant un papillon adhésif à côté d’un autre, sans écart ni superposition, jusqu’à ce que toute la surface du drapeau soit recouverte. Il dénombre la quantité de papillons adhésifs.
Exemple 2
Des élèves comparent la surface de trois cerfs-volants en les couvrant de plusieurs unités de mesure identiques non conventionnelles (mosaïques géométriques). Elles et ils dénombrent la quantité de mosaïques géométriques.
Juxtaposer des unités de mesure permet de quantifier la mesure d’un attribut quelconque d’un objet, habituellement en fonction d’unités de mesure non conventionnelles. Cette stratégie est particulièrement utile pour aider les élèves à développer leur compréhension des attributs longueur, aire et capacité puisque la mesure de chaque attribut est exprimée en fonction d’objets étalons concrets plutôt que d’unités de mesure conventionnelles plus abstraites telles que les centimètres et les mètres. Elle permet aussi de mieux comprendre les concepts d’itération et de structure associée aux unités de mesure.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 91-92.