E2.8 Use appropriate non-standard units to measure area, and explain the effect that gaps and overlaps have on accuracy.
Skill: Use Appropriate Non-standard Units to Measure Area, and Explain the Effect That Gaps and Overlaps Have on Accuracy
According to Van de Walle and Lovin (2008), it is important to make room for estimation in measurement activities because estimation focuses on the attribute to be measured and knowledge of procedures. For example, estimating the area of a book cover using playing cards or sticky notes requires first thinking about what area means and then visualizing a way to use the cards or sticky notes as a unit of area.
In the primary grades, fundamental concepts are essential to the development of the understanding of measurable attributes.
Structure Associated with Units of Measurement
The concept of structure associated with units refers to the way in which these units are organized to determine the size of a given space, whether one-, two-, or three-dimensional. It is closely related to the concept of iteration and is the basis of the juxtaposition strategy used to determine a measurement. The examples below clarify the meaning of this concept using real-world situations.
Example
To determine the area of a rectangle, the units must be iterated in a two-dimensional space, with no gaps or overlaps, so as to cover the rectangle in a rectangular arrangement of columns and rows.
Teachers can assess students' understanding of this concept by asking them, for example, to estimate and then determine the area of a rectangle in which a row and column of squares are drawn.
Students who do not understand the structure associated with the area units do not visualize that the units are organized in an orderly fashion in columns and rows. They tend to cover the area of the rectangle more or less randomly with units of varying size and then have difficulty counting these units.
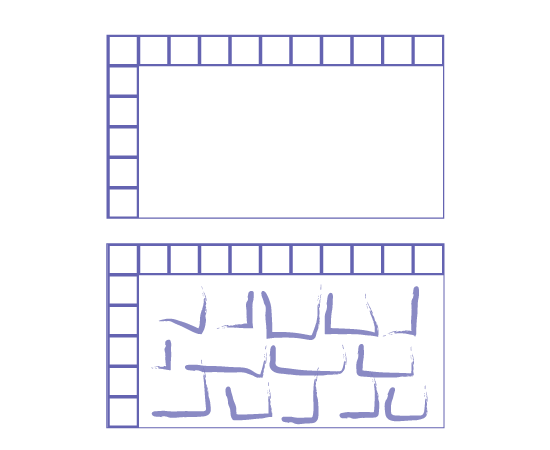Image A rectangular area is filled with a series of squares that run along the length and width. A
rectangular area is filled with a series of squares that run along the length and width. Random patterns fill the
rest of the flat area.
In contrast, students who understand this concept can complete the rectangular layout by juxtaposing square units in columns and rows across the rectangle. They recognize that:
- each column has the same number of square units (for example, 5) and that this number corresponds to the height of the rectangle;
- each row has the same number of square units (for example, 9) and that this number corresponds to the measurement of the base of the rectangle.
This understanding allows them to relate the measurement of the base of a rectangle to its height and area, to explain why the measurement is expressed in square units, and, possibly in the junior grades, to make sense of the common formula for calculating the area of a rectangle. It is important, therefore, to begin understanding this concept in the primary grades.
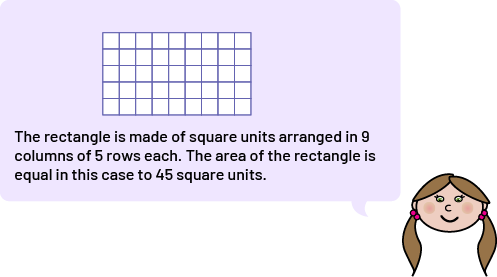Image A grid labeled: "The rectangle is composed of square units arranged in 9 columns of 5 rows each.
The area of the rectangle is equal to 45 square units."
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 17, 57, 58.
Concept of Iteration
The student who understands this concept realizes that it is possible to determine the area by repeatedly superimposing a single non-standard or standard unit of area on it in an orderly fashion.
Example
How many crispy rice squares can you make using one pan if each square covers the space of one sticky note?
Simply place a sticky note in sequence, without gaps or overlaps, over the entire surface of the pan. You can then determine the number of times a sticky note was placed to obtain the surface area of the pan and the number of crispy rice squares.
Source: translated from Fiche attribut Aire, Mat-3e.
Juxtaposition Strategy
Juxtaposing units is the careful placement of a number of concrete objects as units to cover a shape or object to determine its area.
Example 1
A student determines the area of the flag by placing one sticky note next to another, without gaps or overlaps, until the entire surface of the flag is covered. The student counts the number of sticky notes.
Example 2
Students compare the area of three kites by covering them with several identical non-standard units (pattern blocks) and count the number of pattern blocks.
Juxtaposing units quantifies the measurement of any attribute of an object, usually in terms of non-standard units. This strategy is particularly useful in helping students develop their understanding of the attributes length, area, and capacity since the measurement of each attribute is expressed in terms of concrete non-standard units rather than more abstract standard units such as centimetres and metres. It also supports students developing a better understanding of the concepts of iteration and structure associated with units.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 91-92.