E1. Raisonnement géométrique et spatial :
Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure.
Situation d’apprentissage 1 : la chasse aux propriétés
Durée totale : environ 30 minutes
|
Attentes |
Contenus |
|
E1. Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 classer, construire et identifier des cubes, des prismes, des pyramides, des cylindres et des cônes en comparant les faces, les sommets, les arêtes et les angles. |
|
D1. Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne. |
D1.1 trier et classer des ensembles de données portant sur des personnes ou des objets en fonction de deux ou trois attributs, en utilisant des tableaux et des logigrammes, y compris des diagrammes de Venn et de Carroll, et des diagrammes en arbre. |
|
Contexte |
Préalables |
|
Au cycle primaire, l’élève doit pouvoir classer des solides en fonction d’attributs (par exemple, couleur, forme) ou de propriétés (par exemple, nombre d’arêtes, nombre de faces carrées). On doit l’amener à voir les relations entre les solides et les concepts relatifs aux figures planes (par exemple, nom des figures planes et nom des bases). L’élève a d’abord tendance à classer les solides en fonction de leur apparence (par exemple, solides pointus, solides ronds). Graduellement, elle ou il reconnaît qu’un solide est composé de faces ou de surfaces, de sommets et d’arêtes. Alors, l’élève peut commencer à classer les solides en fonction des propriétés des grandes familles de solides. Ainsi naîtra éventuellement le besoin de nommer un ensemble de solides qui ont certaines propriétés très précises (par exemple, les cubes, les cylindres). |
Pour réaliser l’activité, l’élève doit pouvoir reconnaître les faces, les arêtes et les sommets d’un prisme ou d’une pyramide ainsi que les surfaces d’un cône, d’un cylindre ou d’une sphère. L’activité a pour but de permettre à l’élève :
|
Vocabulaire mathématique
cube, prisme à base carrée, prisme à base rectangulaire, pyramide à base triangulaire, pyramide à base carrée, sphère, cône, cylindre, sommet, arête, face, surface, carré, triangle, cercle et rectangle
Matériel
- cerceau
- solides en bois ou en plastique : cubes, prismes à base carrée, prismes à base rectangulaire, pyramides à base triangulaire, pyramides à base carrée, sphères, cônes et cylindres
- sac
- annexe 1I.1
Avant l'apprentissage (mise en train)
À l’intérieur d’un cerceau, placer un cube, un prisme à base carrée, un prisme à base rectangulaire, une pyramide à base triangulaire, une pyramide à base carrée, une sphère, un cône et un cylindre.
Demander aux élèves de s’asseoir autour du cerceau.
Prendre le cube et le montrer aux élèves.
Demander à une ou à un élève de le nommer.
Poser les questions ci-dessous. Demander à l’élève qui répond de justifier sa réponse en touchant le cube à l’endroit approprié.
- Le cube a-t-il des arêtes? Comment le sais-tu?
- Le cube a-t-il des sommets? Comment le sais-tu?
- Le cube a-t-il une face triangulaire? Comment le sais-tu?
Prendre un cylindre et le montrer aux élèves.
Demander à une ou à un élève de le nommer.
Poser les questions ci-dessous. Demander à l’élève qui répond de justifier sa réponse en touchant le cylindre à l’endroit approprié.
- Le cylindre a-t-il des surfaces circulaires? Comment le sais-tu?
- Le cylindre a-t-il des sommets? Comment le sais-tu?
- Le cylindre roule-t-il? Comment le sais-tu?
- Le cylindre a-t-il des faces? Décris-les.
Si cela est nécessaire, procéder de la même façon en utilisant différents solides. Revoir ainsi le vocabulaire associé aux solides.
Pendant l'apprentissage (exploration)
Mettre à la disposition des élèves les solides suivants : des sphères, des cylindres, des cônes, des cubes, des prismes à base carrée, des prismes à base rectangulaire, des pyramides à base triangulaire et des pyramides à base carrée. Dire aux élèves :
- de choisir un solide;
- de s’asseoir en cercle;
- de placer leur solide devant elles et eux.
Mettre tous les énoncés énumérés à l’annexe 1I.1 dans un sac, en prendre un au hasard et le lire.
Demander aux élèves dont le solide possède cet attribut de se lever et de montrer qu’il possède bien l’attribut.
Piger un autre énoncé et procéder de la même façon.
Après l'apprentissage (objectivation/transfert des connaissances)
Poser les questions suivantes.
- Est-ce que tous les solides peuvent rouler?
- Est-ce que tous les solides ont des arêtes?
- Est-ce que tous les solides ont des faces rectangulaires?
- Qu’ont en commun certains solides?
- Qu’ont de différent certains solides?
Exemples de critères d'évaluation
L’élève :
- nomme les solides (cube, prisme à base carrée, prisme à base rectangulaire, cône, cylindre, sphère, pyramide à base triangulaire, pyramide à base carrée);
- reconnaît que le solide a la propriété ou l’attribut nommé;
- compare les solides;
- reconnaît que plusieurs solides ont la même propriété ou le même attribut;
- indique les propriétés des solides (par exemple, le cube a 6 faces, 12 arêtes, 8 sommets);
- utilise les mots sommet, arête, face et surface pour décrire un solide.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison, l’élève peut faire une chasse aux solides en repérant divers objets qui ont la forme d’un cône, d’un cylindre, d’un cube, d’une sphère, d’un prisme à base carrée, d’un prisme à base rectangulaire, d’une pyramide à base triangulaire, d’une pyramide à base carrée.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 73-76.
Situation d’apprentissage 2 : un train solide!
Durée totale : environ 1 h
|
Attentes |
Contenus |
|
E1. Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 classer, construire et identifier des cubes, des prismes, des pyramides, des cylindres et des cônes en comparant les faces, les sommets, les arêtes et les angles. |
|
D1. Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne. |
D1.1 trier et classer des ensembles de données portant sur des personnes ou des objets en fonction de deux ou trois attributs, en utilisant des tableaux et des logigrammes, y compris des diagrammes de Venn et de Carroll, et des diagrammes en arbre. |
Intention pédagogique
L’activité a pour but de permettre à l’élève :
- de comparer un solide avec un autre;
- de trouver des propriétés aux solides;
- de classer les solides selon des attributs plus géométriques, soit les propriétés des familles (par exemple, on regroupe les cylindres parce qu’ils ont des surfaces courbes et non parce qu’ils roulent).
|
Contexte |
Connaissances préalables |
|
En 1re année, l’élève classe les solides selon des attributs observables (solides qui roulent, qui glissent, qui ont le même nombre d’arêtes). Graduellement, elle ou il les classe selon des attributs et des propriétés géométriques. |
Pour réaliser l’activité, l’élève doit pouvoir :
|
Vocabulaire mathématique
cube, sphère, cône, cylindre, prisme, pyramide, propriété, face, surface, sommet, arête, congruent, congru
Matériel
- solides : cubes, cônes, cylindres, sphères, pyramides à base carrée, pyramides à base triangulaire, pyramides à base rectangulaire, pyramides à base pentagonale, pyramides à base hexagonale, pyramides à base octogonale, prismes à base carrée, prismes à base rectangulaire, prismes à base hexagonale
- cartons pour reproduire les locomotives
- feuilles de 28 cm x 43 cm
- ruban adhésif
- colle
- ciseaux
- annexe 2PF.3
- annexe 2PF.4
Avant l'apprentissage (mise en train)
Demander aux élèves de s’asseoir en cercle.
Distribuer un solide à chaque élève.
S’assurer que tous les solides sont représentés.
Demander aux élèves de nommer leur solide.
Dire aux élèves qu’elles et ils vont faire des trains de solides.
Créer une affiche de locomotive, avec l’annexe 2PF.3, sur laquelle est écrite la phrase : « J’ai des sommets. »
Présenter l’affiche à la classe et demander à une ou à un élève de lire la propriété écrite sur la locomotive.
Demander aux élèves si leur solide a cette propriété.
Observer et nommer tous les solides qui ont des sommets.
Poser les questions suivantes :
- Comment se nomme ton solide?
- Pourquoi fait-il partie de ce train?
Demander aux élèves de placer les solides qui ont des sommets au centre de leur cercle de façon à construire un train.
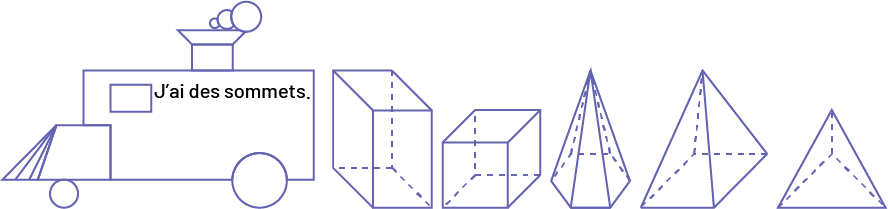 Image Une locomotive construite avec des figures géométriques, à l’intérieur, on peut lire: « J’ai
des sommets. » Derrière la locomotive il y a : « prisme de base rectangulaire », « prisme de base cube ou carré », «
prisme de base hexagonal », « prisme à base carrée », « prisme de base triangulaire. »
Image Une locomotive construite avec des figures géométriques, à l’intérieur, on peut lire: « J’ai
des sommets. » Derrière la locomotive il y a : « prisme de base rectangulaire », « prisme de base cube ou carré », «
prisme de base hexagonal », « prisme à base carrée », « prisme de base triangulaire. »
Faire ressortir que tous les solides du train ont une propriété en commun.
Poser la question suivante : Quelle propriété ces solides ont-ils en commun? ou Comment ces deux solides se ressemblent-ils?
Procéder de la même façon avec d’autres propriétés.
J’ai des surfaces.
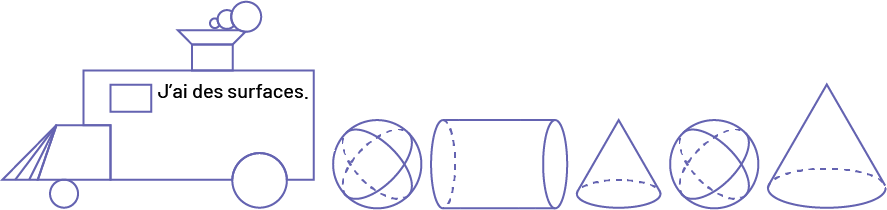 Image Une locomotive construite avec des figures géométriques, à
l’intérieur on peut lire: « J’ai des surfaces. » Derrière la locomotive, il y a : « une sphère », « un cylindre », «
un cône », « une sphère », « un cône plus grand ».
Image Une locomotive construite avec des figures géométriques, à
l’intérieur on peut lire: « J’ai des surfaces. » Derrière la locomotive, il y a : « une sphère », « un cylindre », «
un cône », « une sphère », « un cône plus grand ».
Toutes mes faces sont carrées.
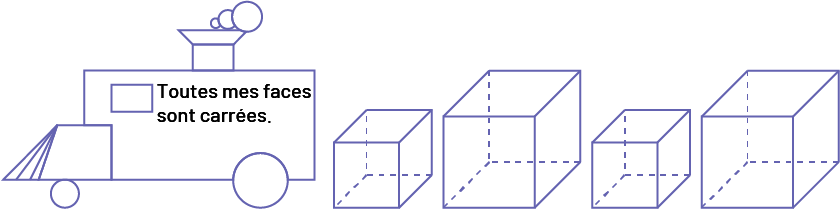 Image Une locomotive construite avec des figures géométriques, à
l’intérieur on peut lire « Toutes mes faces sont carrées. » Suivi de: « un petit cube à base carrée, » « un gros
cube à base carrée, » « un petit cube à base carrée, » « un gros cube à base carrée. »
Image Une locomotive construite avec des figures géométriques, à
l’intérieur on peut lire « Toutes mes faces sont carrées. » Suivi de: « un petit cube à base carrée, » « un gros
cube à base carrée, » « un petit cube à base carrée, » « un gros cube à base carrée. »
J’ai au moins une surface en forme de cercle.
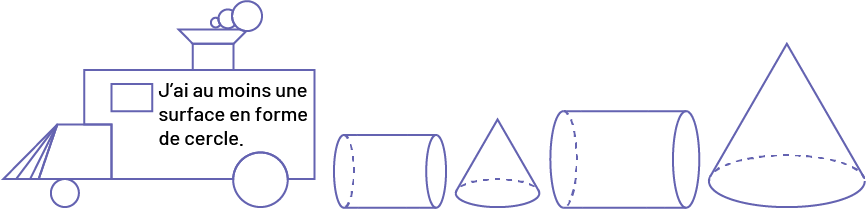 Image Une locomotive construite avec des figures géométriques, à
l’intérieur, on peut lire: « J’ai au moins une surface en forme de cercle. » Suivi de: « un petit cylindre, » « un
gros cylindre, » « un petit cylindre, » « un gros cylindre. »
Image Une locomotive construite avec des figures géométriques, à
l’intérieur, on peut lire: « J’ai au moins une surface en forme de cercle. » Suivi de: « un petit cylindre, » « un
gros cylindre, » « un petit cylindre, » « un gros cylindre. »
J’ai des faces triangulaires.
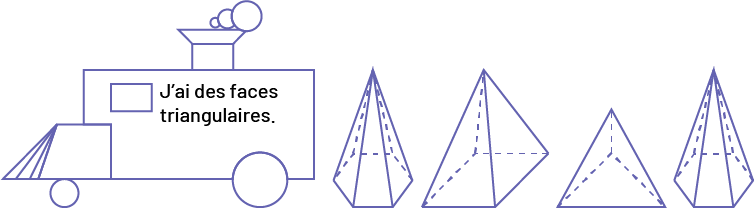 Image Une locomotive construite avec des figures géométriques, à
l’intérieur, on peut lire: « J’ai des faces triangulaires. » Suivi de « une pyramide à base hexagonale, » « une
pyramide à base carrée, » « une pyramide à base triangulaire, » « une pyramide à base hexagonale. »
Image Une locomotive construite avec des figures géométriques, à
l’intérieur, on peut lire: « J’ai des faces triangulaires. » Suivi de « une pyramide à base hexagonale, » « une
pyramide à base carrée, » « une pyramide à base triangulaire, » « une pyramide à base hexagonale. »
Je n’ai aucun sommet.
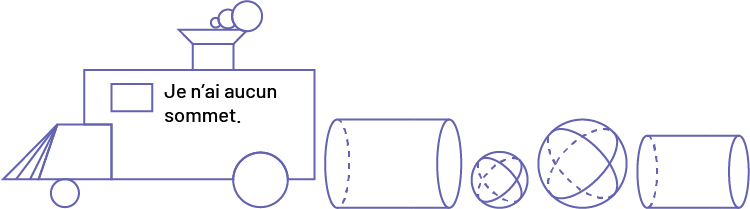 Image Une locomotive construite avec des figures géométriques, à
l’intérieur, on peut lire: « Je n’ai aucun sommet. » Suivi de « un gros cylindre, » « une petite sphère, » « une
grosse sphère, » « un petit cylindre. »
Image Une locomotive construite avec des figures géométriques, à
l’intérieur, on peut lire: « Je n’ai aucun sommet. » Suivi de « un gros cylindre, » « une petite sphère, » « une
grosse sphère, » « un petit cylindre. »
J’ai seulement un sommet.
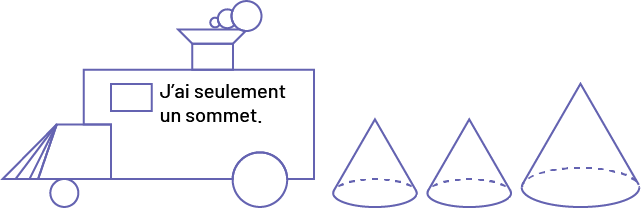 Image Une locomotive construite avec des figures géométriques à
l’intérieur est écrite: « J’ai seulement un sommet. » Suivit de « petits cônes, » « petit cône, » « gros cônes.
»
Image Une locomotive construite avec des figures géométriques à
l’intérieur est écrite: « J’ai seulement un sommet. » Suivit de « petits cônes, » « petit cône, » « gros cônes.
»
J’ai plus de six arêtes.
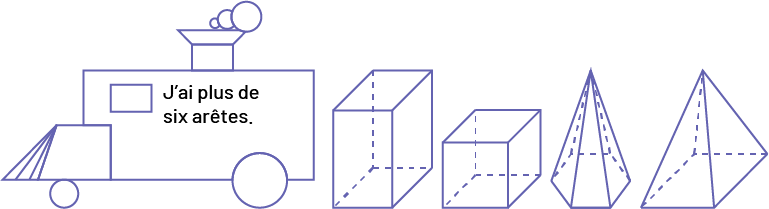 Image Une locomotive construite avec des figures géométriques à
l’intérieur est écrite: « J’ai plus de six arêtes. » Suivi de « un prisme à base rectangulaire, » « un cube, » « une
pyramide à base hexagonale, » « une pyramide à base carrée. »
Image Une locomotive construite avec des figures géométriques à
l’intérieur est écrite: « J’ai plus de six arêtes. » Suivi de « un prisme à base rectangulaire, » « un cube, » « une
pyramide à base hexagonale, » « une pyramide à base carrée. »
Pendant l'apprentissage (exploration)
Dire aux élèves qu’elles et ils vont construire un train dont les wagons seront des solides.
Former des équipes de quatre élèves.
Remettre à chaque équipe des solides et une affiche de locomotive.
Préciser que chaque wagon (solide) doit avoir une propriété en commun avec le wagon qui le précède et une propriété en commun avec le wagon qui le suit.
Montrer un cube et le placer derrière la locomotive.
Demander aux élèves de choisir un solide qui sera le deuxième wagon.
Exemples de solides ayant une propriété en commun avec le cube :
- Le prisme à base carrée, car il a au moins une face carrée.
- La pyramide à base carrée, car elle a au moins deux faces congruentes.
- Le prisme à base rectangulaire, car il a douze arêtes.
Placer le prisme à base carrée après le cube.
Poser les questions suivantes.
- Pourquoi ce solide peut-il suivre le cube?
- Quelle propriété ces solides ont-ils en commun? ou Comment ces solides se ressemblent-ils?
- Quels autres solides peut-on placer après le cube? Pourquoi?
Demander aux élèves de choisir un solide comme troisième wagon.
Exemples de solides ayant une propriété en commun avec le prisme à base carrée :
- La pyramide à base carrée, car elle a au moins une face carrée.
- Le prisme à base rectangulaire, car il a douze arêtes.
Placer la pyramide à base carrée après le prisme à base carrée.
Poser les questions suivantes :
- Pourquoi ce solide peut-il suivre le prisme à base carrée?
- Quelle propriété ces solides ont-ils en commun? ou Comment ces solides se ressemblent-ils?
- Quels autres solides peut-on placer après le prisme à base carrée? Pourquoi? Demander aux élèves de choisir un solide comme quatrième wagon.
Exemples de solides ayant une propriété en commun avec la pyramide à base carrée :
- La pyramide à base triangulaire, car elle a des faces triangulaires.
- Le prisme à base hexagonale, car il a des faces congruentes.
Placer la pyramide à base hexagonale dans le train après la pyramide à base carrée.
Poser les questions suivantes :
- Pourquoi ce solide peut-il suivre la pyramide à base carrée?
- Quelle propriété ces solides ont-ils en commun? ou Comment ces solides se ressemblent-ils?
- Quels autres solides peut-on placer après la pyramide à base carrée? Pourquoi?
Faire remarquer que les solides sont différents l’un de l’autre.
Remettre à chaque équipe de huit à dix solides différents.
Leur demander de construire le plus long train possible avec les solides.
Rappeler aux élèves que chaque wagon est lié au suivant et au précédent par une propriété commune.
Les solides qui ne peuvent pas être inclus dans le train représentent les gens qui regardent passer le train ou les wagons et qui attendent une autre locomotive.
Circuler et intervenir au besoin en posant des questions.
Exemples :
- Pourquoi avez-vous choisi ce solide comme premier wagon?
- Pourquoi peut-on placer ce solide entre ces deux autres solides?
- Y a-t-il un autre solide qui pourrait remplacer ce wagon? Pourquoi?
- Pourquoi ce solide ne peut-il pas faire partie du train?
- Pouvez-vous modifier le train afin d’insérer ce solide?
- Quelle stratégie avez-vous utilisée pour résoudre ce problème?
- Vérifier le train construit par chacune des équipes.
Après l'apprentissage (objectivation/transfert des connaissances)
Remettre à chaque équipe une grande feuille et une copie de l’annexe 2PF.4.
Expliquer aux élèves qu’elles et ils vont représenter leur train en se servant des dessins des solides et du dessin de leur locomotive.
Dire aux élèves :
- de coller la locomotive sur la grande feuille;
- de découper les solides;
- de placer les solides après la locomotive dans le même ordre que ceux du train construit précédemment;
- de placer les dessins des solides non utilisés sous le train.
Exemple
Solides non utilisés :
Demander à une équipe de présenter son train et de justifier l’ordre des wagons en utilisant la terminologie précise (par exemple, noms des solides, propriété commune, solide qui précède, solide qui suit, face, surface, arête, sommet).
Note : Il n’est pas nécessaire que toutes les équipes présentent leur train la même journée. La présentation des trains peut s’étendre sur plusieurs jours. Après toutes les présentations, les trains peuvent être coloriés et plastifiés. Il peut être utile de s’y référer lors de la révision.
Exemples de critères d'évaluation
L’élève :
- nomme les solides classés;
- classe les solides selon un attribut donné ou une propriété donnée;
- compare un solide avec un autre (par exemple, même propriété, propriété différente);
- utilise le vocabulaire approprié dans ses explications (par exemple, pour les attributs : dimensions, couleur, hauteur; pour les propriétés : nombre d’arêtes, de sommets, de faces, de surfaces).
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
Créer un train dont tous les wagons ont une propriété en commun (par exemple, solides qui ont des arêtes, solides qui ont des faces congruentes). |
Demander aux élèves d’observer les trains et de trouver des ressemblances et des différences entre deux wagons (solides). |
Suivi à la maison
À tour de rôle, les élèves peuvent apporter le train de leur équipe à la maison et l’expliquer à leurs parents. La présentation des trains peut aussi être enregistrée et envoyée à la maison.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 119-127.
Situation d’apprentissage 3 : c’est du solide!
Durée totale : environ 3 heures
|
Attentes |
Contenus |
|
E1. Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 classer, construire et identifier des cubes, des prismes, des pyramides, des cylindres et des cônes en comparant les faces, les sommets, les arêtes et les angles. E1.3 reconnaître des longueurs et des angles congrus ainsi que des faces congruentes dans des solides en les superposant, et déterminer si les solides sont congruents. |
|
D1. Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne. |
D1.1 trier et classer des ensembles de données portant sur des personnes ou des objets en fonction de deux ou trois attributs, en utilisant des tableaux et des logigrammes, y compris des diagrammes de Venn et de Carroll, et des diagrammes en arbre. |
Intention pédagogique
L’activité a pour but de permettre à l’élève :
- de construire des coquilles de solides d’après un développement donné;
- de classer des solides à l’aide de diagrammes de Venn en fonction de leurs propriétés.
|
Contexte |
Connaissances préalables |
|
L’élève décrit des prismes, des pyramides et d’autres solides en utilisant le vocabulaire approprié et les compare selon des propriétés. |
Pour réaliser l’activité, l’élève doit pouvoir :
|
Vocabulaire mathématique
développement, coquille, solide, cube, cône, cylindre, sphère, prisme à base carrée, prisme à base rectangulaire, prisme à base pentagonale, prisme à base hexagonale, prisme à base octogonale, pyramide à base carrée, pyramide à base triangulaire, pyramide à base rectangulaire, pyramide à base pentagonale, pyramide à base hexagonale, autres solides, apex, surface courbe, surface plane, face rectangulaire, face triangulaire, face latérale, bases congruentes, sommets, arêtes
Matériel
- ciseaux
- ruban adhésif transparent
- 1 sphère, 1 cône et 1 cylindre par équipe de deux
- 2 cerceaux par équipe de deux
- annexe 3I.1 (a) à (l) sur du papier de bricolage
- annexe 3I.2
- annexe 3I.3 (a) et (b)
Avant l'apprentissage (mise en train)
Former des équipes de deux.
Distribuer à chaque groupe les développements d’un cube, d’un prisme à base carrée et d’une pyramide à base triangulaire sur du papier de bricolage.
Demander aux élèves de construire les trois coquilles de solides en suivant attentivement les directives données.
Il faut :
- découper les développements;
- les plier et les coller;
- écrire ses initiales sur chaque coquille.
Circuler afin de vérifier les constructions et intervenir au besoin en posant des questions.
Exemples
- Quel solide peux-tu construire avec ce développement?
- Combien de faces aura ton solide?
- À quoi servent les lignes pleines?
- À quoi servent les lignes pointillées?
- Comment vas-tu plier ton papier?
- Que vas-tu faire maintenant?
- Quelle est l’étape suivante?
- Laisser à la disposition des élèves les autres développements de prismes et de pyramides.
- Leur demander de construire la coquille des autres solides de sorte que chaque groupe ait un ensemble complet, soit 12 coquilles de solides.
- Allouer un peu de temps chaque jour pour la construction des coquilles de solides.
- Prévoir, dans la classe, un espace de rangement pour les différentes coquilles. Elles serviront à classer des solides dans des diagrammes de Venn.
- Pour chaque équipe, préparer des étiquettes sur lesquelles sont écrites les catégories ci-dessous.
Première série d’étiquettes :
- Les solides
- Les solides ont 12 arêtes et plus
- Les faces latérales des solides sont des rectangles, y compris les carrés
Deuxième série d’étiquettes :
- Les solides
- Toutes les faces latérales sont des triangles
- Toutes les faces latérales sont des rectangles, y compris les carrés
- Toutes les faces sont des carrés congruents
Pendant l'apprentissage (exploration)
Prévoir un espace assez grand pour cette activité.
Former des équipes de deux.
Remettre à chaque équipe une sphère, un cylindre et un cône, deux cerceaux et les deux séries d’étiquettes.
Demander aux élèves :
- de sortir les 12 coquilles de solides qu’elles et ils ont construites;
- de reproduire sur le sol le diagramme de Venn illustré ci-dessous en utilisant les cerceaux et la première série d’étiquettes;
- de classer les solides de leurs ensembles (la sphère, le cylindre et le cône) dans les régions appropriées.
 Image Le diagramme de Venn est formé de trois régions intérieures. Un rectangle qui représente les
solides. Dans le rectangle il y a 2 cercles. Un cercle bleu qui représente les solides qui ont 12 arêtes et plus. Un
cercle rouge qui représente « les faces latérales des solides sont des rectangles incluant les carrés se superpose en
partie ». Les deux cercles se superposent en partie, ainsi un espace se créé pour les solides qui ont les deux
particularités.
Image Le diagramme de Venn est formé de trois régions intérieures. Un rectangle qui représente les
solides. Dans le rectangle il y a 2 cercles. Un cercle bleu qui représente les solides qui ont 12 arêtes et plus. Un
cercle rouge qui représente « les faces latérales des solides sont des rectangles incluant les carrés se superpose en
partie ». Les deux cercles se superposent en partie, ainsi un espace se créé pour les solides qui ont les deux
particularités.
Allouer le temps nécessaire pour leur permettre de réaliser le travail.
Circuler et intervenir au besoin en posant des questions.
Exemples
- Quel est le nom de ce solide?
- Quelles sont les catégories utilisées?
- Ce solide a-t-il la propriété de la catégorie?
- Ce solide a-t-il les propriétés des deux catégories?
- Y a-t-il une région qui est commune aux deux ensembles?
- Dans quelle région vas-tu mettre ce solide? Pourquoi?
- Vérifier le classement de chaque équipe et inciter les élèves à se corriger s’il y a des erreurs.
- S’assurer que les élèves :
- placent les cerceaux sur le sol de manière à ce qu’il y ait une région commune aux deux ensembles;
- placent les étiquettes aux endroits appropriés;
- classent les solides en tenant compte des deux catégories.
Exemple
Le diagramme de Venn est formé de trois régions intérieures et d’une région extérieure. Les étiquettes sont placées à l’extérieur du diagramme.
 Image Le diagramme de Venn est formé de trois régions intérieures. Un
rectangle qui représente les solides. Dans
cet espace uniquement on retrouve : une sphère, un cône, un cylindre, une pyramide à base rectangulaire, une
pyramide à base triangulaire, et une pyramide à base pentagonale. Dans le rectangle il y a 2 cercles.Un cercle bleu
qui représente les solides qui ont 12 arêtes et plus. Dans cet espace uniquement on y retrouve : une
pyramide à base hexagonale. Un cercle rouge qui représente « les faces latérales des solides sont des rectangles
incluant les carrés se superpose en partie ». Dans cet espace uniquement on y retrouve : un prisme à base
rectangulaire.Les deux cercles se superposent en partie, ainsi un espace se créé pour les solides qui ont les deux
particularités. Dans cette espace on retrouve : un prisme à base rectangulaire, un prisme à base hexagonale, un
prisme à base pentagonale, un prisme à base carré, un cube, un prisme à base octogonale.
Image Le diagramme de Venn est formé de trois régions intérieures. Un
rectangle qui représente les solides. Dans
cet espace uniquement on retrouve : une sphère, un cône, un cylindre, une pyramide à base rectangulaire, une
pyramide à base triangulaire, et une pyramide à base pentagonale. Dans le rectangle il y a 2 cercles.Un cercle bleu
qui représente les solides qui ont 12 arêtes et plus. Dans cet espace uniquement on y retrouve : une
pyramide à base hexagonale. Un cercle rouge qui représente « les faces latérales des solides sont des rectangles
incluant les carrés se superpose en partie ». Dans cet espace uniquement on y retrouve : un prisme à base
rectangulaire.Les deux cercles se superposent en partie, ainsi un espace se créé pour les solides qui ont les deux
particularités. Dans cette espace on retrouve : un prisme à base rectangulaire, un prisme à base hexagonale, un
prisme à base pentagonale, un prisme à base carré, un cube, un prisme à base octogonale.
Remettre aux élèves une copie des annexes 3I.2, 3I.3(a) et 3I.3(b).
Leur demander :
- de découper le premier ensemble de solides (annexe 3I.2) et de les coller dans le diagramme 1 de l’annexe 3I.3(a) pour représenter le classement des solides fait sur le sol;
- de découper le second ensemble de solides (annexe 3I.2) et de les coller dans le diagramme 2 de l’annexe 3I.3(b) pour les classer selon les catégories énoncées.
Après l'apprentissage (objectivation/transfert des connaissances)
Faire la mise en commun en posant les questions suivantes.
Diagramme 1
 Image Le diagramme de Venn est formé de trois régions intérieures. Un
rectangle qui représente les solides. Dans
cet espace uniquement on retrouve : une sphère, un cône, un cylindre, une pyramide à base rectangulaire, une
pyramide à base triangulaire, et une pyramide à base pentagonale. Dans le rectangle il y a 2 cercles. Un cercle bleu
qui représente les solides qui ont 12 arêtes et plus. Dans cet espace uniquement on y retrouve :
une pyramide à base hexagonale. Un cercle rouge qui représente « les faces latérales des solides sont des
rectangles incluant les carrés se superpose en partie ». Dans cet espace uniquement on y retrouve : un prisme à
base rectangulaire. Les deux cercles se superposent en partie, ainsi un espace se créé pour les solides qui ont les
deux
particularités. Dans cette espace on retrouve : un prisme à base rectangulaire, un prisme à base hexagonale, un
prisme à base pentagonale, un prisme à base carré, un cube, un prisme à base octogonale.
Image Le diagramme de Venn est formé de trois régions intérieures. Un
rectangle qui représente les solides. Dans
cet espace uniquement on retrouve : une sphère, un cône, un cylindre, une pyramide à base rectangulaire, une
pyramide à base triangulaire, et une pyramide à base pentagonale. Dans le rectangle il y a 2 cercles. Un cercle bleu
qui représente les solides qui ont 12 arêtes et plus. Dans cet espace uniquement on y retrouve :
une pyramide à base hexagonale. Un cercle rouge qui représente « les faces latérales des solides sont des
rectangles incluant les carrés se superpose en partie ». Dans cet espace uniquement on y retrouve : un prisme à
base rectangulaire. Les deux cercles se superposent en partie, ainsi un espace se créé pour les solides qui ont les
deux
particularités. Dans cette espace on retrouve : un prisme à base rectangulaire, un prisme à base hexagonale, un
prisme à base pentagonale, un prisme à base carré, un cube, un prisme à base octogonale.
- Combien y a-t-il de régions dans ce diagramme de Venn?
- Quelles catégories ont été utilisées pour classer les solides dans ce diagramme de Venn?
- Quels sont les solides dont les faces latérales sont des rectangles, y compris les carrés qui ont 12 arêtes et plus?
- Dans quelle région du diagramme ces solides sont-ils placés?
- Quels solides ont 12 arêtes et plus?
- Quel solide a des faces latérales qui sont des rectangles, y compris les carrés, mais a moins de 12 arêtes?
- Quel est le solide dont les faces ne sont pas des rectangles, y compris les carrés qui ont 12 arêtes et plus?
- Pourquoi y a-t-il des solides dans la région extérieure du diagramme?
Diagramme 2
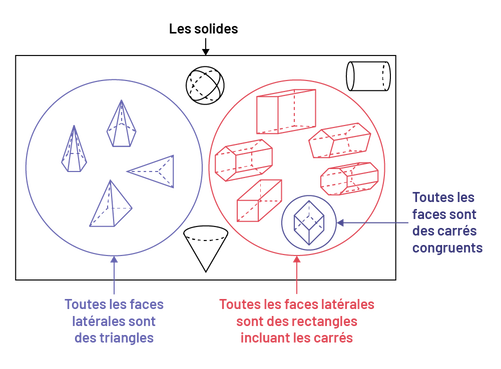 Image Le diagramme de Venn est formé de trois régions intérieures. Un
rectangle qui représente les solides. Dans
cet espace uniquement on retrouve : une sphère, un cône, un cylindre. Dans le rectangle il y a 2 cercles. Un cercle
bleu qui représente les solides qui ont 12 arêtes et plus. Dans cet espace on retrouve : une pyramide à
base hexagonale, une pyramide à base rectangulaire, une pyramide à base triangulaire, et une pyramide à base
pentagonale. Un cercle rouge qui représente « les faces latérales des solides sont des rectangles incluant les
carrés se superpose en partie ». Dans cet espace on y retrouve : un prisme à base rectangulaire, un prisme à base
rectangulaire, un prisme à base hexagonale, un prisme à base pentagonale, un prisme à base carré, un cube dont
toutes les faces des carrés sont congruentes, un prisme à base octogonale.
Image Le diagramme de Venn est formé de trois régions intérieures. Un
rectangle qui représente les solides. Dans
cet espace uniquement on retrouve : une sphère, un cône, un cylindre. Dans le rectangle il y a 2 cercles. Un cercle
bleu qui représente les solides qui ont 12 arêtes et plus. Dans cet espace on retrouve : une pyramide à
base hexagonale, une pyramide à base rectangulaire, une pyramide à base triangulaire, et une pyramide à base
pentagonale. Un cercle rouge qui représente « les faces latérales des solides sont des rectangles incluant les
carrés se superpose en partie ». Dans cet espace on y retrouve : un prisme à base rectangulaire, un prisme à base
rectangulaire, un prisme à base hexagonale, un prisme à base pentagonale, un prisme à base carré, un cube dont
toutes les faces des carrés sont congruentes, un prisme à base octogonale.
- Combien y a-t-il de régions dans ce diagramme de Venn?
- Quelles propriétés ont été utilisées comme catégories pour classer les solides dans ce diagramme de Venn?
- Pourquoi la région étiquetée « Toutes les faces sont des carrés congruents » est-elle à l’intérieur de la région étiquetée « Toutes les faces latérales sont des rectangles, y compris les carrés »?
- Pourquoi les deux régions étiquetées « Toutes les faces latérales sont des triangles » et « Toutes les faces latérales sont des rectangles, y compris les carrés » ne se touchent-elles pas?
- Pourquoi la sphère, le cône et le cylindre sont-ils dans la région extérieure du diagramme?
- Si tu remplaçais les propriétés énoncées comme catégories sur les étiquettes par le nom des solides, lesquels pourrais-tu utiliser?
- Comment les prismes se ressemblent-ils?
- Comment les prismes sont-ils différents?
- Le cube est-il un prisme? Pourquoi?
- Comment les pyramides se ressemblent-elles?
- Comment les pyramides sont-elles différentes?
Exemples de critères d'évaluation
L’élève :
- construit des coquilles de solides;
- nomme les prismes en fonction de leurs bases;
- nomme les pyramides en fonction de leurs bases;
- classe les solides selon les catégories énoncées;
- classe chaque solide dans la région appropriée du diagramme de Venn;
- compare les solides les uns aux autres;
- décrit leurs différences et leurs ressemblances;
- décrit les propriétés de chaque grande famille de solides.
- Les pyramides ont au moins quatre sommets. Leurs faces latérales sont triangulaires. Elles ont seulement une base.
- Les prismes ont tous deux bases congruentes. Leurs faces latérales sont des rectangles, y compris les carrés.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 137-144.
