E1. Geometric and Spatial Reasoning
Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them.
Learning Situation 1: Property Hunting
Total duration: approximately 30 minutes
|
Overall Expectations |
Specific Expectations |
|
E1. Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them. |
E1.1 Sort, construct, and identify cubes, prisms, pyramids, cylinders, and cones by comparing their faces, edges, vertices, and angles. |
|
D1. Manage, analyse, and use data to make convincing arguments and informed decisions, in various contexts drawn from real life. |
D1.1 Sort sets of data about people or things according to two and three attributes, using tables and logic diagrams, including Venn, Carroll, and tree diagrams, as appropriate. |
|
Learning Goals |
|
The purpose of the activity is to enable the student to:
|
|
Learning Context |
Prerequisites |
|
In the primary grades, students should be able to sort three-dimensional objects according to attributes (for example, color, shape) or properties (for example, number of edges, number of square faces), and to see the relationships between three-dimensional objects and two-dimensional shape concepts (for example, names of two-dimensional shapes and names of bases). The student initially tends to sort three-dimensional objects according to their appearance (for example, pointy three-dimensional objects, round three-dimensional objects). Gradually, they recognize that a three-dimensional object is composed of faces or surfaces, vertices and edges. Then, the student can begin to sort three-dimensional objects according to geometric properties. Eventually, the need to name a set of three-dimensional objects that have certain very specific properties will arise (for example, cubes, cylinders). |
To complete the activity, students must be able to identify the faces, edges and vertices of a prism or pyramid, and the surfaces of a cone, cylinder or sphere. |
Material
- hoop
- wooden or plastic three-dimensional objects: cubes, square-based prisms, rectangle-based prism, triangle-based pyramid, square-based pyramids, spheres, cones and cylinders
- bag
- Appendix 1.1
Mathematical Vocabulary
cube, square-based prism, rectangle-based prism, triangle-based pyramid, square-based pyramid, sphere, cone, cylinder, vertex, edge, face, surface, square, triangle, circle, and rectangle
Before Learning (Warm-Up)
Place a cube, square-based prism, rectangle-based prism, triangle-based pyramid, square-based pyramid, sphere, cone, and cylinder inside a hoop.
Have students sit around the hoop.
Take the cube and show it to the students.
Ask a student to name it.
Ask the questions below and have the student who answers justify the answer by touching the cube in the appropriate place.
- Does the cube have edges? How do you know?
- Does the cube have vertices? How do you know?
- Does the cube have a triangular face? How do you know?
Take a cylinder and show it to the students.
Ask a student to name it.
Ask the questions below and have the student who answers justify their answer by touching the cylinder in the appropriate place.
- Does the cylinder have circular surfaces? How do you know?
- Does the cylinder have vertices? How do you know?
- Does the cylinder roll? How do you know?
- Does the cylinder have faces? Describe them.
If necessary, proceed in the same way using different three-dimensional objects. Review the vocabulary associated with three-dimensional objects.
Active Learning (Exploration)
Provide students with the following three-dimensional objects: spheres, cylinders, cones, cubes, square-based prisms, rectangle-based prism, triangle-based pyramid and square-based pyramids. Tell students to:
- choose a three-dimensional object;
- sit in a circle;
- place their three-dimensional object in front of them.
Put all the statements listed in Appendix 1.1 in a bag, pick one at random and read it.
Ask students if their three-dimensional object has the attribute.
Pick another statement and proceed in the same way.
Consolidation of Learning
Ask the following questions.
- Can all three-dimensional objects roll?
- Do all three-dimensional objects have edges?
- Do all three-dimensional objects have rectangular faces?
- Are there some three-dimensional objects that share an attribute?
- Are there some three-dimensional objects that have a unique attribute?
Examples of Success Criteria
The student:
- names the three-dimensional objects (cubes, prisms, cones, cylinders, pyramids);
- recognizes that the three-dimensional object has the named property or attribute;
- uses faces, edges, vertices, and angles to compare these three-dimensional objects;
- sorts these three-dimensional objects by comparing their faces, edges, vertices, and angles;
- uses the words vertex, edge, face and angle to describe these three-dimensional objects.
Differentiated Instruction
The activity can be modified to meet different student needs.
|
To Facilitate the Task |
To Enrich the Task |
|
|
Follow-Up at Home
At home, students can go on a three-dimensional object hunt by locating various objects that are shaped like a cone, cylinder, cube, sphere, square-based prism, rectangle-based prism, triangle-based pyramid, square-based pyramid.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 73-76.
Learning Situation 2: A Three-Dimensional Train!
Total duration: approximately 1 hour
|
Overall Expectations |
Specific Expectations |
|
E1. Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them. |
E1.1 Sort, construct, and identify cubes, prisms, pyramids, cylinders, and cones by comparing their faces, edges, vertices, and angles. |
|
D1. Manage, analyse, and use data to make convincing arguments and informed decisions, in various contexts drawn from real life. |
D1.1 Sort sets of data about people or things according to two and three attributes, using tables and logic diagrams, including Venn, Carroll, and tree diagrams, as appropriate. |
|
Learning Goals |
|
The purpose of the activity is to enable the student to:
|
|
Learning Context |
Prerequisites |
| In Grade 1, students sort three-dimensional objects according to observable attributes (for example, three-dimensional objects that roll, slide, have the same number of edges) and gradually sort them according to geometric attributes and properties. | To complete the activity, the student must be able to:
|
Material
- three-dimensional objects: cubes, cones, cylinders, spheres, square-based pyramids, triangle-based pyramids, rectangle-based pyramids, pentagon-based pyramids, hexagon-based pyramids, octagon-based pyramids, square-based prisms, rectangle-based prisms, hexagon-based prisms
- cardboard boxes to represent the locomotives
- sheets of 28 cm x 43 cm paper
- adhesive tape
- glue
- scissors
- Appendix 2PF.3
- Appendix 2PF.4
Mathematical Vocabulary
cube, sphere, cone, cylinder, prism, square-based prism, rectangle-based prism, hexagon-based prism, pyramid, square-based pyramid, triangle-based pyramid, rectangle-based pyramid, pentagon-based pyramid, hexagon-based pyramid, octagon-based pyramid, property, face, surface, vertex, edge, congruent
Before Learning (Warm-Up)
Ask students to sit in a circle.
Distribute a three-dimensional object to each student and ask them to think about how we would name it.
Ensure that all three-dimensional objects have been assigned.
Tell students that they will be making trains of three-dimensional objects.
Create a locomotive poster, using Appendix 2PF.3, with the phrase, “I have vertices.”
Present the poster to the class and ask a student to read the property written on the locomotive.
Ask students if their three-dimensional object has this property and to place it inside the circle if it does.
Ask the following questions of the students who placed their three-dimensional object in the circle:
- What is the name of your three-dimensional object?
- Why is it part of this train?
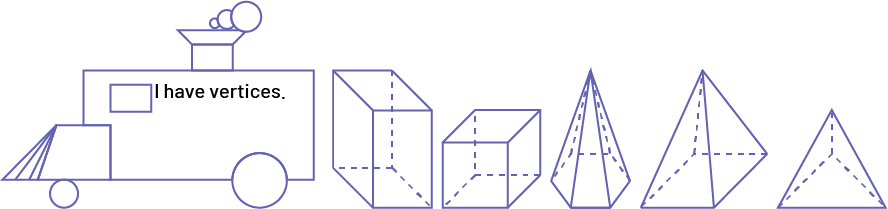 Image A locomotive made of geometric shapes, inside is labeled: "I have vertices." The following are next to the locomotive: "prism with a rectangular base", "prism with a cube or square base", "prism with a hexagonal base", "prism with a square base", "prism with a triangular base."
Image A locomotive made of geometric shapes, inside is labeled: "I have vertices." The following are next to the locomotive: "prism with a rectangular base", "prism with a cube or square base", "prism with a hexagonal base", "prism with a square base", "prism with a triangular base."
Point out that all the three-dimensional objects in the train have one property in common.
Ask the following question: How are these two three-dimensional objects similar?
Proceed in the same way with other properties.
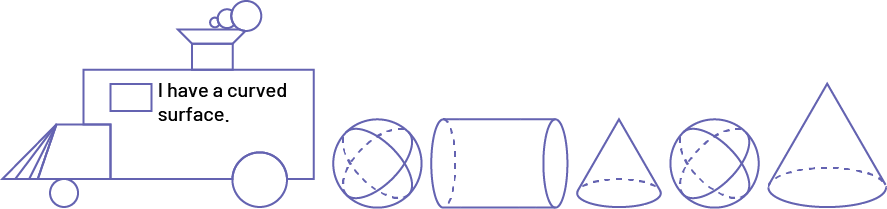
I have a curved surface.
All my faces are squares.
 Image A locomotive built with geometric shapes inside is labeled: "All my sides are square." Followed by, "a small square-based cube," "a large square-based cube," "a small square-based cube," "a large square-based cube."
Image A locomotive built with geometric shapes inside is labeled: "All my sides are square." Followed by, "a small square-based cube," "a large square-based cube," "a small square-based cube," "a large square-based cube."
I have at least one circle-shaped face.
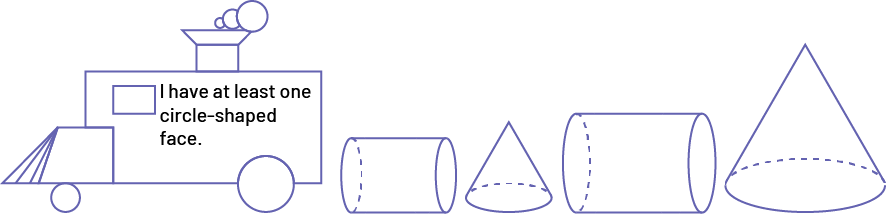 Image A locomotive built with geometric shapes inside is labeled: "I have at least one circle-shaped surface." Followed by: "a small cylinder," "a large cylinder," "a small cylinder," "a large cylinder."
Image A locomotive built with geometric shapes inside is labeled: "I have at least one circle-shaped surface." Followed by: "a small cylinder," "a large cylinder," "a small cylinder," "a large cylinder."
I have triangular faces.
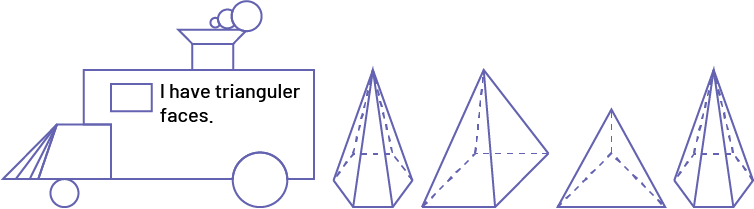 Image A locomotive built with geometric shapes, inside is labeled: "I have triangular faces." Followed by "a hexagonal-based pyramid," "a square-based pyramid," "a triangular-based pyramid," "a hexagonal-based pyramid."
Image A locomotive built with geometric shapes, inside is labeled: "I have triangular faces." Followed by "a hexagonal-based pyramid," "a square-based pyramid," "a triangular-based pyramid," "a hexagonal-based pyramid."
I have no vertices.
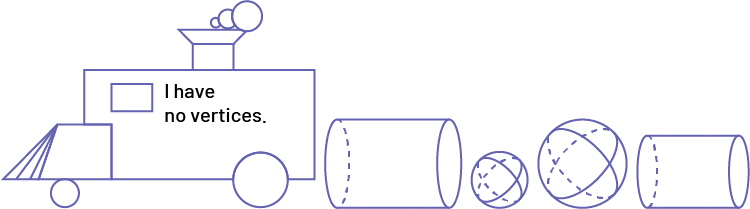 Image A locomotive built with geometric shapes, inside is labeled: "I have no vertex." Followed by "a large cylinder," "a small sphere," "a large sphere," "a small cylinder."
Image A locomotive built with geometric shapes, inside is labeled: "I have no vertex." Followed by "a large cylinder," "a small sphere," "a large sphere," "a small cylinder."
I only have one vertex.
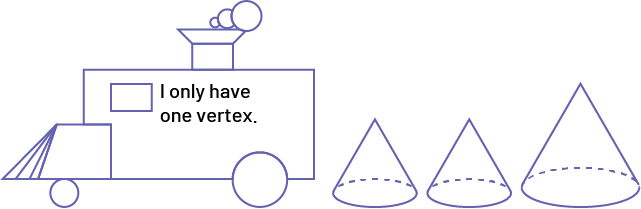 Image A locomotive built with geometric shapes inside is labeled: "I only have one vertex." Followed by "small cones," "small cone," "large cones."
Image A locomotive built with geometric shapes inside is labeled: "I only have one vertex." Followed by "small cones," "small cone," "large cones."
I have more than six edges.
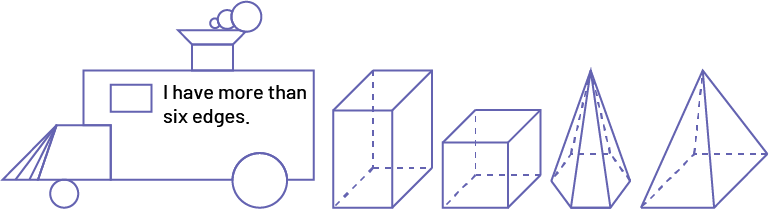 Image A locomotive built with geometric shapes inside is labeled: "I have more than six edges." Followed by "a prism with a rectangular base," "a cube," "a pyramid with a hexagonal base," "a pyramid with a square base."
Image A locomotive built with geometric shapes inside is labeled: "I have more than six edges." Followed by "a prism with a rectangular base," "a cube," "a pyramid with a hexagonal base," "a pyramid with a square base." Active Learning (Exploration)
Specify that each car (three-dimensional object) must have something in common with the car in front of it, and something in common with the car behind it.
Form teams of four students.
Provide each team with three-dimensional objects and a locomotive poster.
Specify that each car (three-dimensional object) must have one property in common with the car in front of it and one property in common with the car behind it.
Show a cube and place it behind the locomotive.
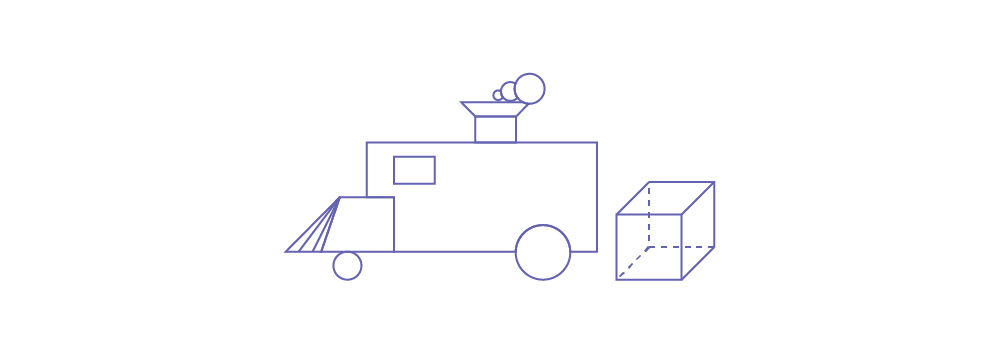
Ask students to choose a three-dimensional object to be the second car.
Examples of three-dimensional objects with a property in common with the cube:
- The square-based prism, because it has at least one square face.
- The square-based pyramid, because it has at least two congruent faces.
- The rectangle-based prism, because it has twelve edges.
Place the square-based prism after the cube.
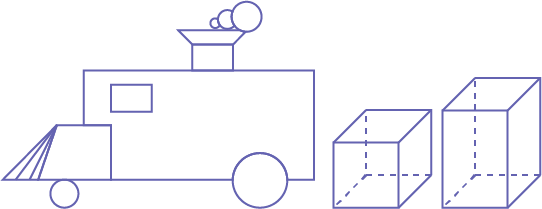
Ask the following questions.
- Why can this three-dimensional object follow the cube?
- How are these three-dimensional objects similar?
- What other three-dimensional objects can be placed after the cube? Why?
Ask students to choose a three-dimensional object as the third car.
Examples of three-dimensional objects with a property in common with the square-based prism:
- The square-based pyramid, because it has at least one square face.
- The rectangle-based prism, because it has twelve edges.
Place the square-based pyramid after the square-based prism.
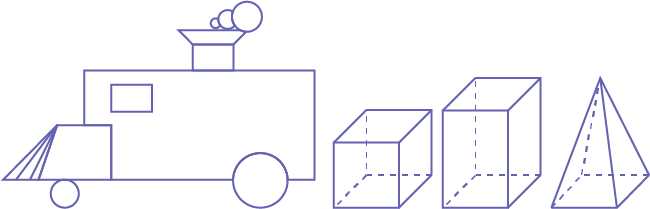 Image A locomotive built with geometric shapes followed by "a cube," "a prism with a rectangular base," "a pyramid with a square base."
Image A locomotive built with geometric shapes followed by "a cube," "a prism with a rectangular base," "a pyramid with a square base."
Ask the following questions:
- Why can this three-dimensional object follow the square-based prism?
- How are these three-dimensional objects similar?
- What other three-dimensional objects can be placed after the square-based prism? Why? Ask students to choose a three-dimensional object as the fourth car.
Examples of three-dimensional objects that have a property in common with the square-based pyramid:
- The pyramid with a triangular base, because it has triangular faces.
- The hexagonal based prism, because it has congruent faces.
Place the hexagonal based pyramid in the train after the square based pyramid.
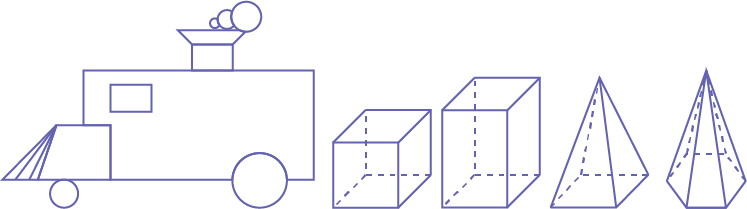 Image A locomotive built with geometric shapes followed by "a cube," "a rectangular-based prism," "a square-based pyramid," "a hexagonal-based pyramid."
Image A locomotive built with geometric shapes followed by "a cube," "a rectangular-based prism," "a square-based pyramid," "a hexagonal-based pyramid."
Ask the following questions:
- Why can this three-dimensional object follow the square-based pyramid?
- How are these three-dimensional objects similar?
- What other three-dimensional objects can be placed after the square-based pyramid? Why?
Point out that the three-dimensional objects are different from each other.
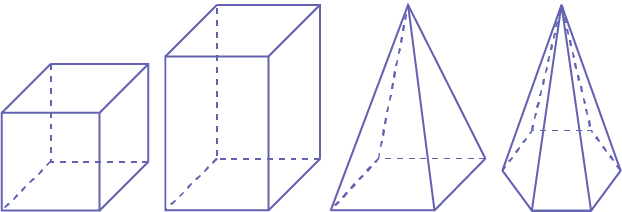
Give each team eight to ten different three-dimensional objects.
Ask them to build the longest train possible with the three-dimensional objects.
Remind students that each car is linked to the next and the previous one by something they have in common.
The three-dimensional objects that cannot be included in the train represent people watching the train or cars go by and waiting for another locomotive.
Circulate and provide support as needed, by asking questions such as:
- Why did you choose this three-dimensional object as your first car?
- Why can we place this three-dimensional object between these two cars?
- Is there another three-dimensional object that could replace this car? Why?
- Why can't this three-dimensional object be part of the train?
- Can you modify the train to insert this three-dimensional object?
- What strategy did you use to solve this problem?
Check the train built by each team.
Consolidation of Learning
Provide each team with a large sheet of paper and a copy of Appendix 2PF.4.
Explain to students that they are going to represent their train using the drawings of the three-dimensional objects and their locomotive.
Tell students:
- to glue the locomotive on the large sheet;
- to cut out the three-dimensional objects;
- to place the three-dimensional objects after the locomotive in the same order as those in the train constructed earlier;
- to place the drawings of the unused three-dimensional objects under the train.
Example
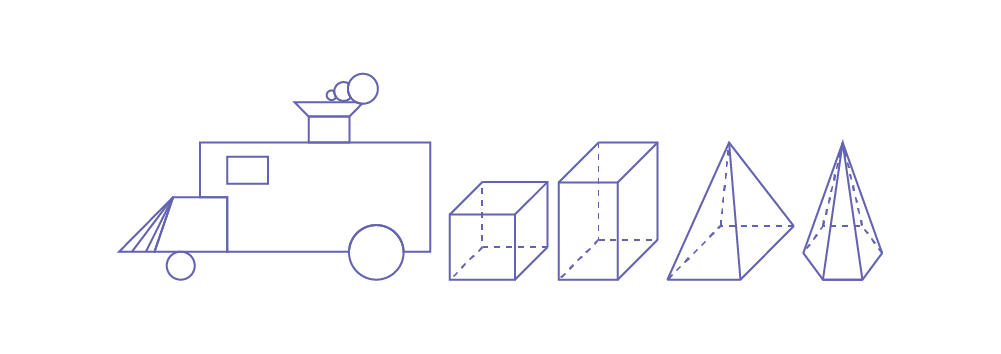 Image locomotive built with geometric shapes followed by "a cube," "a rectangular-based prism," "a square-based pyramid," "a hexagonal-based pyramid."
Image locomotive built with geometric shapes followed by "a cube," "a rectangular-based prism," "a square-based pyramid," "a hexagonal-based pyramid."
Unused three-dimensional objects:
Have a team present their train and justify the order of the cars using specific terminology (for example, names of three-dimensional objects, common property, three-dimensional object that precedes, three-dimensional object that follows, face, surface, edge, vertex).
Note: It is not necessary for all teams to present their trains on the same day. The presentation of the trains can take place over several days. After all the presentations, the trains can be colored and laminated. It may be useful to refer to them when reviewing.
Examples of Success Criteria
The student:
- names the sorted three-dimensional objects;
- sorts three-dimensional objects according to a given attribute or a given property;
- compares one three-dimensional object with another (for example, same property, different property);
- uses appropriate vocabulary in explanations (for example, for attributes: dimensions, color, height; for properties: number of edges, vertices, faces, surfaces).
Differentiated Instruction
The activity can be modified to meet the needs of the students.
|
To Facilitate the Task |
To Enrich the Task |
|
Create a train whose cars all have a common property (for example, three-dimensional objects that have edges, three-dimensional objects that have congruent faces). |
Have students observe the trains and find similarities and differences between two cars (three-dimensional objects). |
Follow-Up at Home
Students can take turns taking their team's train home and explaining it to their parents, or the train presentation can be recorded and sent home.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 119-127.
Learning Situation 3: It’s Three-Dimensional!
Total duration: approximately 3 hours
|
Overall Expectations |
Specific Expectations |
|
E1. Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them. |
E1.1 Sort, construct, and identify cubes, prisms, pyramids, cylinders, and cones by comparing their faces, edges, vertices, and angles. E1.3 Identify congruent lengths, angles, and faces of three-dimensional objects by mentally and physically matching them, and determine if the objects are congruent. |
|
D1. Manage, analyse, and use data to make convincing arguments and informed decisions, in various contexts drawn from real life. |
D1.1 Sort sets of data about people or things according to two and three attributes, using tables and logic diagrams, including Venn, Carroll, and tree diagrams, as appropriate. |
|
Learning Goals |
The purpose of the activity is to enable the student to:
|
|
Learning Context |
Prerequisite |
| Students will describe prisms, pyramids, and other three-dimensional objects using appropriate vocabulary and compare them based on properties. | To complete the activity, the student must be able to:
|
Materials
- scissors
- transparent adhesive tape
- 1 sphere, 1 cone and 1 cylinder per team of two
- 2 hoops per team of two
- Appendix 3I.1 (a) to (l) on construction paper
- Appendix 3I.2
- Appendix 3I.3 (a) and (b)
Mathematical Vocabulary
net, three-dimensional object, cube, cone, cylinder, sphere, square-based prism, rectangle-based prism, pentagon-based prism, hexagon-based prism, square-based pyramid, triangle-based pyramid, rectangle-based pyramid, pentagon-based pyramid, hexagon-based pyramid, other three-dimensional objects, apex, curved surface, flat surface, rectangular face, triangular face, side face, congruent bases, vertices, edges.
Before Learning (Warm-Up)
Form teams of two.
Distribute nets of a cube, a square-based prism and a triangle-based pyramid to each group on construction paper.
Have students build the three three-dimensional objects by carefully following the instructions given.
You must:
- cut out the nets;
- fold and glue them;
- write your initials on each object.
Circulate to check constructions and provide support if necessary by asking questions.
Examples
- What three-dimensional object can you build with this net?
- How many faces will your three-dimensional object have?
- What are the solid lines for?
- What are the dotted lines for?
- How will you fold your paper?
- What will you do now?
- What is the next step?
First Set of Labels:
- Three-dimensional objects
- Three-dimensional objects with 12 or more edges
- The side faces of three-dimensional objects are rectangles, including squares
Second Set of Labels:
- Three-dimensional objects
- All side faces are triangles
- All side faces are rectangles, including squares
- All faces are congruent squares
Active Learning (Exploration)
Provide a large enough space for this activity.
Form teams of two.
Give each team a sphere, a cylinder and a cone, two hoops and the two sets of labels.
Ask students to:
- take out the 12 three-dimensional objects that they have built;
- make a Venn diagram on the floor using two hoops and the first set of labels.
- sort their set of three-dimensional objects (including the sphere, the cylinder and the cone) into the appropriate regions.
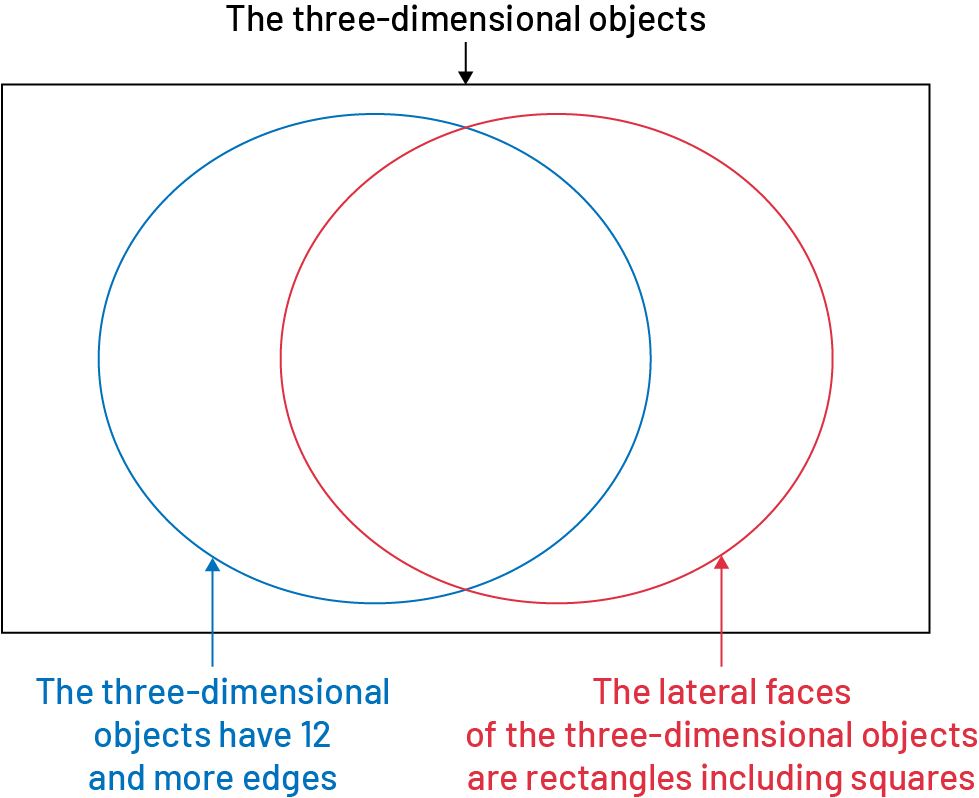 Image A Venn diagram made up of three interior parts. A rectangle that represents solids. Inside the rectangle there are 2 circles. A blue circle that represents solids that have 12 or more edges. A red circle that represents "the side faces of the solids are rectangles including squares that partly overlap". The two circles overlap in part, so a space is created for the solids that have both features.
Image A Venn diagram made up of three interior parts. A rectangle that represents solids. Inside the rectangle there are 2 circles. A blue circle that represents solids that have 12 or more edges. A red circle that represents "the side faces of the solids are rectangles including squares that partly overlap". The two circles overlap in part, so a space is created for the solids that have both features.
Allocate the necessary time for them to complete the work.
Circulate and provide support as needed, by asking questions such as:
- What is the name of this three-dimensional object?
- What categories are you using to sort your set of three-dimensional objects?
- Does this three-dimensional object fit the category?
- Does this three-dimensional object have the properties of it?
- Is there a region that is common to both sets?
- In which region will you put this three-dimensional object? Why?
Check how each team sorted the objects and encourage students to correct themselves if there are any mistakes.
Ensure that students:
- place the hoops on the floor so that there is a common area for both sets;
- place the labels in the appropriate places;
- sort the three-dimensional objects by taking into account the two categories.
Example
The Venn diagram consists of three inner regions and one outer region. The labels are placed on the outside of the diagram.
 Image A Venn diagram made up of three interior regions. A rectangle that represents solids. In this space only there is a sphere, a cone, a cylinder, a pyramid with a rectangular base, a pyramid with a triangular base, and a pyramid with a pentagonal base. In the rectangle there are 2 circles. A blue circle represents the solids that have 12 or more edges. In this space only there is: a pyramid with a hexagonal base. A red circle that shows "the side faces of the solids are rectangles with squares partly overlapping". In this space only there is: a prism with a rectangular base. The two circles partly overlap, so a space is created for the solids that have both characteristics. In this space we find: a prism with a rectangular base, a prism with a hexagonal base, a prism with a pentagonal base, a prism with a square base, a cube, a prism with an octagonal base.
Image A Venn diagram made up of three interior regions. A rectangle that represents solids. In this space only there is a sphere, a cone, a cylinder, a pyramid with a rectangular base, a pyramid with a triangular base, and a pyramid with a pentagonal base. In the rectangle there are 2 circles. A blue circle represents the solids that have 12 or more edges. In this space only there is: a pyramid with a hexagonal base. A red circle that shows "the side faces of the solids are rectangles with squares partly overlapping". In this space only there is: a prism with a rectangular base. The two circles partly overlap, so a space is created for the solids that have both characteristics. In this space we find: a prism with a rectangular base, a prism with a hexagonal base, a prism with a pentagonal base, a prism with a square base, a cube, a prism with an octagonal base.
Provide students with a copy of Appendices 3I.2, 3I.3(a) and 3I.3(b).
Ask them to:
- cut out the first set of three-dimensional objects (Appendix 3I.2) and paste them into Diagram 1 in Appendix 3I.3(a) to represent the classification of three-dimensional objects made on the floor;
- cut out the second set of three-dimensional objects (Appendix 3I.2) and paste them into Diagram 2 in Appendix 3I.3(b) to sort them according to the stated categories.
Consolidation of Learning
Share the results by asking the following questions.
Diagram 1
 Image A Venn diagram made up of three interior regions. A rectangle that represents solids. In this space only there is a sphere, a cone, a cylinder, a pyramid with a rectangular base, a pyramid with a triangular base, and a pyramid with a pentagonal base. In the rectangle there are 2 circles. A blue circle represents the solids that have 12 or more edges. In this space only there is: a pyramid with a hexagonal base. A red circle that shows "the side faces of the solids are rectangles with squares partly overlapping". In this space only there is: a prism with a rectangular base. The two circles partly overlap, so a space is created for the solids that have both characteristics. In this space we find: a prism with a rectangular base, a prism with a hexagonal base, a prism with a pentagonal base, a prism with a square base, a cube, a prism with an octagonal base.
Image A Venn diagram made up of three interior regions. A rectangle that represents solids. In this space only there is a sphere, a cone, a cylinder, a pyramid with a rectangular base, a pyramid with a triangular base, and a pyramid with a pentagonal base. In the rectangle there are 2 circles. A blue circle represents the solids that have 12 or more edges. In this space only there is: a pyramid with a hexagonal base. A red circle that shows "the side faces of the solids are rectangles with squares partly overlapping". In this space only there is: a prism with a rectangular base. The two circles partly overlap, so a space is created for the solids that have both characteristics. In this space we find: a prism with a rectangular base, a prism with a hexagonal base, a prism with a pentagonal base, a prism with a square base, a cube, a prism with an octagonal base.
- How many regions are there in this Venn diagram?
- What categories were used to sort the three-dimensional objects in this Venn diagram?
- Which three-dimensional objects have side faces that have 12 or more edges?
- In what region of the diagram are these three-dimensional objects placed?
- Which three-dimensional objects have 12 or more edges?
- Which three-dimensional object has faces that are rectangles, including squares, but has fewer than 12 edges?
- Which three-dimensional object has faces that are not rectangles, and 12 or more edges?
- Why are there three-dimensional objects in the outer region of the diagram?
Diagram 2
 Image A Venn diagram consists of three inner parts. A rectangle that represents solids. In this space only there are: a sphere, a cone, a cylinder. In the rectangle there are 2 circles. A blue circle representing solids with 12 or more edges. In this space there are: a pyramid with a hexagonal base, a pyramid with a rectangular base, a pyramid with a triangular base, and a pyramid with a pentagonal base. A red circle which shows "the lateral faces of the solids are rectangles including the squares partly overlapping". In this space there is: a prism with a rectangular base, a prism with a rectangular base, a prism with a hexagonal base, a prism with a pentagonal base, a prism with a square base, a cube with all the faces of the squares being congruent, a prism with an octagonal base
Image A Venn diagram consists of three inner parts. A rectangle that represents solids. In this space only there are: a sphere, a cone, a cylinder. In the rectangle there are 2 circles. A blue circle representing solids with 12 or more edges. In this space there are: a pyramid with a hexagonal base, a pyramid with a rectangular base, a pyramid with a triangular base, and a pyramid with a pentagonal base. A red circle which shows "the lateral faces of the solids are rectangles including the squares partly overlapping". In this space there is: a prism with a rectangular base, a prism with a rectangular base, a prism with a hexagonal base, a prism with a pentagonal base, a prism with a square base, a cube with all the faces of the squares being congruent, a prism with an octagonal base
- How many regions are there in this Venn diagram?
- What categories were used to sort the three-dimensional objects in this Venn diagram?
- Why is the region labeled “All faces are congruent squares” inside the region labeled “All the lateral faces of the three-dimensional objects are rectangles, including squares”?
- Why don't the two regions labeled “All the lateral faces are triangles” and “All the lateral faces of the three-dimensional objects are rectangles, including squares” touch?
- Why are the sphere, cone, and cylinder in the outer region of the diagram?
- If you replaced the categories listed as categories on the labels with the names of the three-dimensional objects, which ones could you use?
- How are the prisms similar?
- How are the prisms different?
- Is the cube a prism? Why?
- How are the pyramids similar?
- How are the pyramids different?
Examples of Success Criteria
The student:
- constructs three-dimensional objects;
- names the prisms according to their bases;
- names the pyramids according to their bases;
- sorts three-dimensional objects according to the given categories;
- sorts each three-dimensional object into the appropriate region of the Venn diagram;
- compares three-dimensional objects to each other;
- describes their differences and similarities;
- describes the properties of each major family of three-dimensional objects.
- Pyramids have at least four vertices. Their side faces are triangular. They have only one base.
- All prisms have two congruent bases; their side faces are rectangles, including squares.
Differentiated Instruction
|
To Facilitate the Task |
To Enrich the Task |
|
|
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 137-144.
