E2. Sens de la mesure :
Comparer, estimer et déterminer des mesures dans divers contextes.
SITUATION D’APPRENTISSAGE 1 : AILES DE PAPIER
Durée totale : environ 1 h 45 min
Sommaire
Dans cette situation d’apprentissage, les élèves comparent et mesurent l’aire de la surface de cerfs-volants de différentes façons à l’aide de mosaïques géométriques.
|
Attente |
Contenus |
|
E2. Comparer, estimer et déterminer des mesures dans divers contextes. |
E2.5 Utiliser des unités de mesure de tailles différentes pour mesurer le même attribut d’un objet donné et démontrer que même si l’utilisation de différentes unités de mesure donne des résultats différents, la taille de l’attribut reste inchangée. E2.7 Comparer les aires de figures planes en les faisant correspondre, en les superposant ou en les décomposant et les recomposant, et démontrer que différentes figures peuvent avoir la même aire. E2.8 Utiliser des unités de mesure non conventionnelles appropriées pour mesurer l’aire et expliquer l’incidence du chevauchement et des espaces entre les unités sur l’exactitude de la mesure. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à choisir des unités de mesure non conventionnelles appropriées pour mesurer l’aire d’une surface;
- à utiliser convenablement l’unité de mesure choisie.
|
Contexte pédagogique |
Préalables |
|
Au cycle primaire, les élèves développent le sens de la mesure. À cette fin, les activités proposées par le personnel enseignant doivent reposer sur des contextes authentiques, solliciter l’utilisation de matériel de manipulation et souligner l’importance de la mesure dans la vie de tous les jours. Les élèves explorent et s’approprient les attributs longueur, aire, masse et capacité en utilisant d’abord des unités de mesure non conventionnelles. La démarche consiste à déterminer l’attribut à mesurer, à choisir une unité de mesure appropriée pour la tâche à accomplir, à comparer l’attribut de l’unité choisie avec l’attribut de l’objet à mesurer pour en déterminer la mesure et enfin à communiquer le résultat. Pour mesurer l’aire d’une surface, les élèves doivent connaître ce qu’est une surface (par exemple, un plan à deux dimensions) et ce qu’est l’aire d’une surface (la grandeur d’une surface ou d’un espace à deux dimensions). Ensuite, elles et ils doivent choisir une unité de mesure de surface appropriée (par exemple, la face d’un cube) pour mesurer une surface choisie (par exemple, l’aire de la surface de leur pupitre), déterminer le nombre d’unités nécessaires (unités carrées) pour la couvrir et communiquer le résultat en utilisant des termes justes. Ce n’est qu’après avoir compris le sens conceptuel de l’attribut et la signification de mesurer un attribut que les élèves peuvent utiliser des unités de mesure conventionnelles. |
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
surface, superposer, objet étalon, surface ayant la plus grande aire, surface ayant la plus petite aire, surfaces ayant des aires égales ou semblables à, ordonner
Matériel
- mosaïques géométriques en plastique ou en bois et en papier
- mosaïques géométriques sur le tableau interactif
- bâtonnets de colle (deux par équipe)
- annexe 1.1 (une copie)
- annexe 1.2 (une copie par élève)
- annexe 1.3,annexe 1.4, annexe 1.5, annexe 1.6 (copies suffisantes pour toutes les équipes)
- annexe 1.7 (une copie par élève)
- rubans
- tiges de bois
- ficelle
- illustration de courtepointes
- papier de couleur (rouge, bleu, jaune, orange, beige, vert)
- tableau interactif
- grand carton blanc
Activité préparatoire
Durée : environ 15 minutes
Former des équipes et remettre à chaque équipe des mosaïques géométriques en quantité suffisante. Demander aux élèves de décrire les différentes mosaïques géométriques sans mettre l’accent sur la terminologie juste. Poursuivre en leur demandant de recouvrir l’aire de la surface d’un trapèze en utilisant des mosaïques géométriques. Souligner aux élèves que les pièces qui recouvrent l’aire de la surface sont juxtaposées et qu’il n’y a ni espace ni chevauchement entre ces pièces. Comparer les solutions obtenues (par exemple, les élèves recouvrent l’aire de la surface du trapèze avec trois triangles verts, ou encore un losange bleu et un triangle vert). Continuer l’exercice en recouvrant l’aire de la surface d’un losange bleu et ensuite l’aire de la surface d’un hexagone jaune de différentes mosaïques géométriques.
Cette activité pourrait être reprise ultérieurement en utilisant d’autres figures géométriques composées de deux ou de plusieurs mosaïques géométriques (par exemple, un hexagone et deux trapèzes).

Avant l’apprentissage (mise en train)
Lire aux élèves la lettre d’une grand-maman prénommée Mihn qui vit au Canada depuis un an (annexe 1.1). Lors de la lecture, présenter l’illustration de l’annexe 1.2.
Discuter du message contenu dans la lettre en posant des questions telles que :
- Que nous demande grand-maman Mihn? (Elle demande de trouver le nombre de formes géométriques nécessaires pour fabriquer un cerf-volant.)
- Comment allons-nous déterminer la quantité de formes géométriques nécessaire pour confectionner le cerf-volant? (Nous pourrions fabriquer un cerf-volant et le recouvrir avec des mosaïques géométriques.)
- À quoi ressemble la forme du cerf-volant que grand-maman Mihn nous a envoyé? (Il ressemble à un losange, une des mosaïques géométriques.)
- Comment allons-nous trouver la solution à la question de grand-maman Mihn? (Nous allons recouvrir le cerf-volant de mosaïques géométriques.)
- Comment allons-nous transmettre la solution à grand-maman Mihn? (Nous allons lui écrire un courriel et lui envoyer quelques photos.)




Pendant l’apprentissage (exploration)
Durée : environ 60 minutes
Dans un premier temps, modeler le recouvrement de l’aire de la surface d’une figure à l’aide de mosaïques géométriques sur le tableau interactif. Établir des liens avec l’activité préparatoire.
Familiariser les élèves avec cette activité en posant des questions telles que :
- Comment peut-on recouvrir cette surface?
- Peut-on laisser des espaces entre les mosaïques géométriques? Pourquoi?
- Peut-on superposer les mosaïques géométriques? Pourquoi?
- Peut-on utiliser toutes les formes de mosaïques géométriques?
Bien faire comprendre aux élèves que lorsqu’on recouvre une surface, il ne faut pas qu’il y ait de chevauchement et d’espace entre les formes géométriques.
Dans un deuxième temps, former des équipes.
Remettre à chaque équipe :
- quatre losanges de même grandeur que celui de l’annexe 1.2 (cerfs-volants) préalablement découpés dans du carton blanc rigide;
- une quantité suffisante de toutes les formes de mosaïques géométriques en plastique ou en bois et une quantité suffisante de mosaïques géométriques en papier de couleur découpées à partir des annexes 1.3, 1.4, 1.5 et 1.6;
- deux bâtonnets de colle;
- deux copies de l’annexe 1.7.
Demander aux élèves de chaque équipe de superposer les quatre cerfs-volants afin qu’elles et ils constatent que l’aire de la surface de chaque cerf-volant est de la même grandeur. Demander ensuite à chaque élève de recouvrir deux cerfs-volants de deux façons différentes à l’aide de mosaïques géométriques en plastique ou en bois.
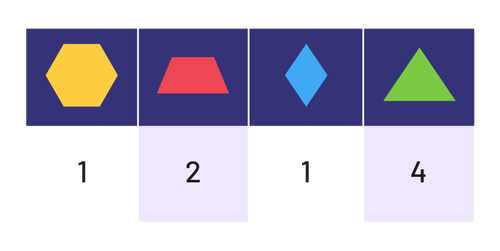
Présenter l’annexe 1.7 aux élèves et les inviter à inscrire, dans les tableaux, le nombre de mosaïques géométriques utilisées pour recouvrir chaque cerf-volant. Demander, par la suite, de remplacer chaque mosaïque géométrique en plastique ou en bois par une mosaïque géométrique en papier de forme équivalente, et de coller cette dernière.

Comme cette activité fait appel à la motricité fine des élèves, on peut y apporter certaines modifications afin de leur faciliter la tâche. Par exemple, utiliser des mosaïques géométriques autocollantes vendues chez différents fournisseurs de matériel scolaire.
Circuler parmi les élèves et poser des questions telles que :
- En quoi vos cerfs-volants sont-ils différents? (Ils ne sont pas recouverts du même nombre ou de la même forme de mosaïques géométriques.)
- Est-ce que les mosaïques géométriques recouvrent toute l’aire de la surface?
- Est-ce que vous avez bien noté, dans le tableau de dénombrement, le nombre de mosaïques géométriques utilisées pour chaque forme?
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 15 minutes
Rassembler les élèves et les inviter, en équipe, à présenter leurs cerfs-volants et leurs tableaux de dénombrement.
Animer une discussion sur les différentes façons de recouvrir une même surface en posant les questions suivantes :
- Si vous regardez vos quatre cerfs-volants, quelle mosaïque géométrique avez-vous utilisée le plus souvent? le moins souvent?
- Quels renseignements peut-on tirer des tableaux de dénombrement? (Ils indiquent le nombre de mosaïques géométriques utilisées pour recouvrir chaque cerf-volant.)
- Lorsque vous avez recouvert les cerfs-volants de mosaïques géométriques, qu’avez-vous mesuré? (Nous avons mesuré l’aire de la surface des cerfs-volants.)
- Pour mesurer l’aire de la surface d’un cerf-volant, est-ce que toutes les mosaïques géométriques doivent se toucher? Pourquoi? (Oui, pour qu’il n’y ait pas de surface non recouverte sur les cerfs-volants ou parce qu’il faut mesurer toute l’aire de la surface du cerf-volant.)
- Est-ce que tous les cerfs-volants ont une surface de même grandeur? Comment le savez-vous? (Oui, lorsque nous les superposons, ils sont de la même grandeur.)
- Alors, comment expliquer que les résultats inscrits dans vos tableaux de dénombrement sont parfois différents, alors que l’aire de la surface des cerfs-volants est la même? (Nous avons utilisé des mosaïques géométriques différentes.)
- Comment vérifier que votre tableau de dénombrement correspond bien à votre cerf-volant? (Les nombres dans mon tableau correspondent aux mosaïques géométriques collées sur mon cerf-volant.)
- Quelles mosaïques géométriques faut-il à grand-maman Mihn pour fabriquer son cerf-volant en tissu? (Il lui faudra quatre formes différentes : des triangles, des trapèzes, des losanges [les bleus] et des hexagones. Elle n’aura pas besoin de carrés ni de losanges beiges, car nous n’avons pas eu à les utiliser pour recouvrir les cerfs-volants.)
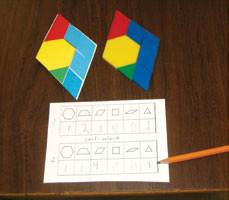
 Image Des élèves sont assis par terre. Devant eux ils, il y a une feuille de papier et des mosaïques
géométriques. Deux cerfs-volants de chaque côté d’une feuille qui explique les mosaïques qui ont été utilisées et
leur nombre.
Image Des élèves sont assis par terre. Devant eux ils, il y a une feuille de papier et des mosaïques
géométriques. Deux cerfs-volants de chaque côté d’une feuille qui explique les mosaïques qui ont été utilisées et
leur nombre.
Faire observer aux élèves, à l’aide des tableaux de dénombrement, que le nombre de mosaïques géométriques varie selon la grandeur des formes utilisées. Plus la forme est petite, plus il en faudra pour couvrir l’aire de la surface d’un cerf-volant. Les élèves doivent comprendre que la grandeur de l’aire de la surface ne change pas, même si le nombre de mosaïques qui la recouvrent varie.
Prolongement
Assembler tous les cerfs-volants confectionnés par les élèves en un grand cerf-volant collectif. Pour ce faire, coller les cerfs-volants sur un grand carton, encadrer le grand cerf-volant collectif avec des tiges de bois pour le solidifier et y apposer un ruban décoratif.
 Image Situation de classe avec deux enfants. Un garçon qui tient la ficelle
du cerf-volant, on voit des rubans de différentes couleurs. La fille tient le grand cerf-volant qui est recouvert de
différentes mosaïques géométriques.
Image Situation de classe avec deux enfants. Un garçon qui tient la ficelle
du cerf-volant, on voit des rubans de différentes couleurs. La fille tient le grand cerf-volant qui est recouvert de
différentes mosaïques géométriques.
Animer une discussion en posant des questions telles que :
- Combien de petits cerfs-volants ont servi à la confection du grand cerf-volant?
- Combien avons-nous utilisé de mosaïques géométriques pour couvrir l’aire de la surface du grand cerf-volant? (Il serait possible de dénombrer les mosaïques géométriques de tous les tableaux de dénombrement.)
- Quelle mosaïque géométrique trouve-t-on en plus grand nombre sur notre grand cerf-volant?
- Pouvez-vous relever des régularités sur le cerf-volant? Lesquelles?
- En observant votre grand cerf-volant, que répondriez-vous à grand-maman Mihn?
- Quelle grandeur de tissu grand-maman Mihn aura-t-elle besoin? (Elle aura besoin d’un morceau de tissu de la grandeur de notre grand cerf-volant.)
- Combien de mosaïques géométriques grand-maman Mihn aura-t-elle besoin?
Amener les élèves à réaliser que la réponse dépendra des formes que grand-maman Mihn utilisera pour fabriquer son grand cerf-volant. Les élèves pourraient donner des réponses comme celles-ci :
- Si grand-maman Mihn utilise seulement des hexagones, il lui en faudra moins, car l’hexagone couvre une plus grande surface que le triangle ou le losange.
- Si elle utilise seulement des triangles, il lui en faudra plus, car le triangle couvre une plus petite surface que l’hexagone ou le losange.
- Si elle utilise seulement des losanges, il lui faudra plus de losanges que d’hexagones, mais moins de losanges que de triangles, car le losange couvre une plus petite surface que l’hexagone, mais une plus grande surface que le triangle.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison, les élèves peuvent :
- recouvrir des surfaces à l’aide de différents objets (carrés de papier ou de tissu);
- chercher des objets dont l’aire de la surface est 5 fois ou 10 fois plus grande que celle de la surface d’un objet étalon préalablement choisi.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 122-129.
Situation d’apprentissage 2 : des gâteaux pas comme les autres!
Durée totale : environ 2 h 30 min
Sommaire
Dans cette situation d’apprentissage, les élèves développent leur compréhension conceptuelle des attributs longueur et aire. À la suite de la construction de rectangles ayant un même périmètre, mais des mesures d’aire différentes, elles et ils assemblent des formes géométriques pour construire une nouvelle forme ayant le plus grand périmètre possible. Ensuite, elles et ils comparent l’aire de la surface des formes des diverses équipes.
|
Attente |
Contenus |
|
E2. Comparer, estimer et déterminer des mesures dans divers contextes. |
E2.1 Utiliser des unités de mesure de longueur appropriées pour estimer, mesurer et comparer les périmètres de polygones et de lignes courbes fermées, et construire des polygones ayant un périmètre donné. E2.8 Utiliser des unités de mesure non conventionnelles appropriées pour mesurer l’aire et expliquer l’incidence du chevauchement et des espaces entre les unités sur l’exactitude de la mesure. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à comprendre que des rectangles qui ont le même périmètre n’ont pas nécessairement des surfaces qui ont la même aire;
- à reconnaître que l’orientation d’une figure ne change ni le périmètre ni l’aire de sa surface.
|
Contexte pédagogique |
Préalables |
|
L’apprentissage de la mesure en 3e année marque un passage important, soit le recours aux unités de mesure conventionnelles du Système international d’unités pour déterminer la longueur et le périmètre de la surface d’objets. Dans cette situation d’apprentissage, l’objectif du personnel enseignant est d’amener les élèves à comprendre ce que signifie « déterminer le périmètre d’un objet et mesurer l’aire d’une surface ». L’activité proposée repose sur un contexte authentique et requiert des élèves qu’elles et ils utilisent le matériel de manipulation ainsi que les instruments de mesure appropriés. Essentiellement centrée sur la mesure des attributs longueur (périmètre) et aire de même que sur les limites des unités de mesure non conventionnelles, cette activité facilite une transition vers les unités de mesure conventionnelles. |
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
aire de la surface, surface, longueur, périmètre, contour, centimètre, unité carrée, unité de mesure, attribut de mesure
Matériel
- ficelle mesurant de 80 cm à 90 cm et dont les bouts sont attachés (une par équipe)
- deux feuilles de papier quadrillé (1 cm sur 1 cm) collées ensemble (une par équipe)
- marqueurs (trois couleurs différentes par équipe)
- feuilles volantes
- papillons adhésifs
- ruban adhésif
- ciseaux
- ensembles de 12 formes géométriques de grand format (un ensemble par équipe)
- cordes à sauter
- tangram (un par équipe)
- annexe 3.1 (une par équipe)
- règle (une par équipe)
Activité préparatoire
Durée : environ 60 minutes
Prévoir, pour chaque équipe, une ficelle d’une longueur de 80 cm à 90 cm et dont les bouts sont attachés.
Former des équipes. Amorcer une discussion avec les élèves pour vérifier leurs connaissances des attributs périmètre et aire.
Remettre à chaque équipe une ficelle, trois marqueurs de couleurs différentes, des feuilles de papier quadrillé en centimètres carrés et une règle pour tracer des lignes droites.
Demander aux élèves d’utiliser toute la ficelle sans défaire le nœud pour former successivement trois rectangles de dimensions diverses sur leur papier quadrillé, d’en tracer le contour de différentes couleurs et d’inscrire les mesures du périmètre et de l’aire de la surface sur l’annexe 3.1 – Feuille de route.


Circuler parmi les équipes, observer leur travail et intervenir, au besoin, pour aider des élèves à consolider leur compréhension des concepts de périmètre et de l’aire d’une surface.
|
Observations possibles |
Interventions possibles |
|
Un groupe n'utilise pas toute la ficelle pour créer le rectangle. 
|
Rappeler aux élèves la consigne qu'il faut tracer le rectangle en utilisant toute la ficelle. Demander aux élèves pourquoi cette directive est importante (par exemple, Il faut utiliser toute la ficelle afin de garder la même longueur de ficelle pour le contour de tous les rectangles.) |
|
Un groupe peine à déterminer l'aire de la surface, car il trouve le nombre de carrés trop élevé. 
|
Demander aux élèves s’il leur est possible de déterminer l'aire de la surface sans dénombrer tous les carrés (par exemple, diviser le rectangle en sections, compter les unités carrées de chaque section, ensuite additionner les unités carrées de toutes les sections). |
|
Un groupe fait un quadrilatère, mais oublie qu'un rectangle a des angles droits. 
|
Demander aux élèves de nommer les propriétés d'un rectangle et d'expliquer si le quadrilatère tracé présente ces propriétés. |
|
Un groupe a de la difficulté à déterminer le périmètre des rectangles tracés. 
Pour trouver le périmètre, les élèves comptent tous les carrés autour du rectangle jaune. 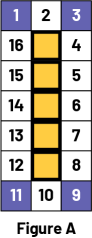
|
Poser des questions, telles que :
Leur faire comprendre qu'aucun des côtés des carrés sur les coins de la figure ne correspond à un côté du rectangle jaune défini par la ficelle. Leur faire observer que même si la ficelle touche plusieurs carrés ce n'est pas l'unité carrée qu'il faut compter, mais les côtés des carrés qui touchent la ficelle. 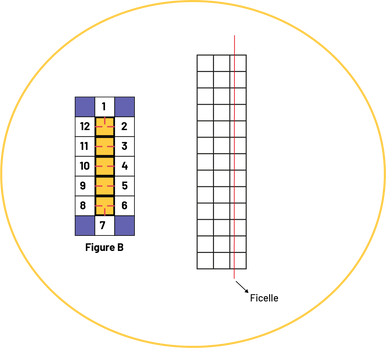 Image Une figure « A », est composée de 5 carrés jaunes, est encadré par d’autres carrés
bleus et blancs.
Ces autres carrés sont numérotés de, un à 16, les angles sont représentés par les carrés bleus. Un quadrillé
est à côté de la figure « A », il est composé de 3 colonnes de 13 carrés. Une ficelle rouge
traverse le quadrillé sur la longueur. Le tout est encerclé en jaune. Image Une figure « A », est composée de 5 carrés jaunes, est encadré par d’autres carrés
bleus et blancs.
Ces autres carrés sont numérotés de, un à 16, les angles sont représentés par les carrés bleus. Un quadrillé
est à côté de la figure « A », il est composé de 3 colonnes de 13 carrés. Une ficelle rouge
traverse le quadrillé sur la longueur. Le tout est encerclé en jaune.
Si nécessaire, défaire la ficelle et l'étendre sur une ligne de la feuille quadrillée et ne compter que les longueurs des carrés. |
Préparer un tableau de compilation des résultats de la classe. Pour ce faire, demander à une ou à un membre de chaque équipe d’inscrire les résultats de leur feuille de route sur ce tableau.
Demander ensuite à certaines équipes d’expliquer la façon dont elles ont fait pour tracer leurs rectangles. L’élève utilise le tableau interactif pour montrer sa démarche et traite de l’importance d’utiliser des repères à chaque sommet afin de conserver les angles droits, de tenir la ficelle bien tendue et d’utiliser une règle pour tracer des lignes droites.
Présenter le tableau de compilation rempli :
Exemple
|
Rectangle |
Périmètre |
Aire |
Longueur des côtés |
|
Équipe verte R1 |
86 cm |
156 unités carrées |
\(4 + 4 + 39 + 39 \) |
|
Équipe verte R2 |
86 cm |
330 unités carrées |
\(10 + 10 + 33 + 33 \) |
|
Équipe verte R3 |
86 cm |
460 unités carrées |
\(20 + 20 + 23 + 23 \) |
|
Équipe or R1 |
82 cm |
40 unités carrées |
1 cm, 40 cm, 1 cm, 40 cm |
|
Équipe or R2 |
82 cm |
78 unités carrées |
2 cm, 39 cm, 2 cm, 39 cm |
|
Équipe or R3 |
82 cm |
348 unités carrées |
12 cm, 29 cm, 12 cm, 29 cm |
|
Équipe violette R1 |
80 cm |
175 unités carrées |
5 cm, 35 cm, 5 cm, 35 cm |
|
Équipe violette R2 |
80 cm |
300 unités carrées |
10 cm, 30 cm, 10 cm, 30 cm |
|
Équipe violette R3 |
80 cm |
400 unités carrées |
4 côtés de 20 cm |
Légende : R1 représente le rectangle 1, R2 le rectangle 2 et R3 le rectangle 3.
Utiliser les résultats inscrits dans le tableau de compilation pour consolider les connaissances des élèves quant aux concepts du périmètre et de l’aire de la surface.
Poser des questions telles que :
- Comment avez-vous déterminé le périmètre? (Nous avons déterminé le périmètre en comptant le nombre d’unités de longueur de chaque côté du rectangle.)
- Que remarquez-vous au sujet du périmètre des rectangles de chaque équipe? (Tous les rectangles d’une même équipe ont le même périmètre.)
- Selon vous, pourquoi avez-vous obtenu ces résultats? (Nous avons obtenu ces résultats parce que la ficelle de chaque équipe ne change pas de longueur, elle produit toujours le même périmètre.)
- Que remarquez-vous au sujet de l’aire de la surface des rectangles de chaque équipe? (L’aire de la surface de tous les rectangles d’une même équipe est différente.)
- Comment avez-vous procédé pour déterminer l’aire de la surface?


- Que remarquez-vous au sujet de la longueur des côtés de chacun des rectangles?
Voici des exemples possibles de réponses d’élèves :
- Même si les côtés des trois rectangles sont de longueurs différentes, la somme de la mesure des côtés demeure la même.
- Chaque rectangle a deux paires de côtés de même longueur.
- Plus la longueur d’une paire de côtés augmente, plus la longueur de l’autre paire de côtés diminue.
- Quels liens établissez-vous entre la longueur des côtés et le périmètre? (La somme des longueurs des côtés est égale au périmètre.)
Note : Le carré est un rectangle puisqu’il possède deux paires de côtés de même longueur.
Avant l’apprentissage (mise en train)
Durée : environ 10 minutes
Avant la mise en train, préparer des images de gâteaux fantaisistes découpées dans des magazines ou trouvées dans Internet. Afficher au tableau ou au mur les images des gâteaux avant l’arrivée des élèves en classe. Poser quelques questions aux élèves pour les aider à indiquer les différentes formes géométriques utilisées pour faire les gâteaux.
Présenter aux élèves la situation-problème suivante :
 Image
Dans un encadré, des photos de gâteaux sont accompagnées du texte suivant : « Les grandes cheffes et les grands
chefs participent périodiquement à des compétitions de gâteaux. Imagine que cette année, pour la rencontre de la
société des As des mathématiques, on lance le défi de créer un superbe gâteau composé de formes géométriques.
»
Image
Dans un encadré, des photos de gâteaux sont accompagnées du texte suivant : « Les grandes cheffes et les grands
chefs participent périodiquement à des compétitions de gâteaux. Imagine que cette année, pour la rencontre de la
société des As des mathématiques, on lance le défi de créer un superbe gâteau composé de formes géométriques.
»
Pendant l’apprentissage (exploration)
Durée : environ 60 minutes
Idéalement, cette activité devrait se dérouler au gymnase.
Préparer plusieurs ensembles de 12 formes géométriques de grand format.
Chaque ensemble doit contenir les mêmes formes.
Les formes géométriques de grand format sont découpées dans de grandes pièces de polystyrène (matériau offert dans un magasin d’articles de bureau) ou sont en carton. Les formes peuvent être des quadrilatères, des triangles ou d’autres polygones. Tous les côtés des formes doivent être droits. Il est important que les élèves puissent facilement comparer les formes pour déterminer le plus grand périmètre.

Faire asseoir les élèves en cercle, et remettre à chacune et à chacun une forme géométrique des ensembles de grand format.
Inviter les élèves à placer leur pièce devant elles et eux pour qu’elle soit bien visible.
Demander aux élèves si elles et ils estiment que leur pièce a le plus grand périmètre.
Inviter les autres élèves à manifester leur accord ou leur désaccord.
Quelques élèves auront les mêmes formes géométriques puisque les ensembles sont seulement composés de 12 formes.
Cette activité donne l’occasion de faire ressortir les limites des unités de mesure non conventionnelles (par exemple, manque de précision) et de proposer une transition vers les unités de mesure conventionnelles.
Former des équipes et leur demander de déterminer la pièce qui a le plus grand périmètre. Il est très important que les élèves vérifient et justifient leur choix en utilisant une unité de mesure non conventionnelle, telle une corde à sauter. Demander aux élèves de présenter leurs résultats et de décrire leur démarche pour comparer les périmètres.
Recueillir les formes pour refaire les 12 ensembles de départ.
Former des équipes différentes et remettre à chaque équipe un ensemble de 12 formes géométriques de grand format qui représentent des morceaux de gâteau à assembler.
Expliquer aux élèves les critères à respecter.
- Le gâteau est formé de 8 des 12 formes géométriques distribuées.
- Le contour du gâteau est une ligne fermée.
- Les côtés des figures utilisées doivent être juxtaposés.
- Le gâteau a le plus grand périmètre possible.
Circuler parmi les équipes, observer le travail et poser des questions telles que :
- Pourquoi avez-vous choisi ces formes? (Nous avons choisi les huit formes qui ont le plus grand périmètre.)
- Comment allez-vous vérifier que votre gâteau a bien le plus grand périmètre possible? (Nous allons essayer différents agencements et les mesurer tous ou peut-être que nous allons d’abord juxtaposer les formes avec les plus grands périmètres et ensuite ajouter les autres.)
- Y aurait-il une autre façon d’organiser les formes de sorte que le périmètre de votre gâteau soit plus grand? (Il faut essayer de juxtaposer seulement un côté de chaque forme pour obtenir le plus grand périmètre.)
- Pour obtenir un plus grand périmètre, pourriez-vous remplacer l’une des formes choisies par l’une des formes non choisies? (Il faut vérifier que la forme non choisie a un plus grand périmètre que la forme qu’elle remplace.)
|
Observations possibles |
Interventions possibles |
|
L'équipe ne choisit pas les pièces ayant le plus grand périmètre. 
|
Le personnel enseignant demande aux élèves de justifier leur choix et les guide dans la mesure des périmètres de chaque forme géométrique à l'aide d'une ficelle ou d'une autre unité de mesure. |
|
L'équipe assemble les pièces de sommet à sommet ou de sommet à arête et non en juxtaposant les côtés des formes. 
|
Le personnel enseignant rappelle aux élèves que le contour du gâteau doit être une ligne fermée. (Une ligne fermée est une ligne dont les deux extrémités se touchent. Une partie du côté d'une pièce doit correspondre à une partie du côté d'une autre pièce.) 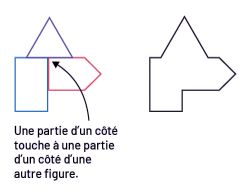
|
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 30 minutes
Demander à chaque équipe de présenter son gâteau et d’expliquer ses choix de formes géométriques et la démarche suivie pour assembler le gâteau. Une fois les présentations terminées, poser des questions aux équipes et profiter de l’échange mathématique pour consolider les connaissances des concepts des élèves.
|
Présentations par équipe |
Pistes de questionnement |

L'équipe présente un gâteau dont les pièces ont plusieurs côtés adjacents. |
Au début, lorsqu'on vous a demandé de déterminer la forme ayant le plus grand périmètre, quelles ont été vos observations concernant les dimensions de cette pièce? (La forme géométrique avec le plus grand périmètre était longue et mince.) Votre gâteau a-t-il une forme semblable? Comment pouvez-vous modifier votre gâteau pour obtenir un plus grand périmètre? 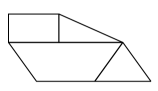
|
|
L'équipe présente un gâteau long et mince. 
|
« Votre gâteau répond-il à tous les critères? » « Comment en avez-vous déterminé le périmètre? » «Est-il possible de modifier votre gâteau pour obtenir un plus grand périmètre? » |
|
L'équipe a utilisé une corde à sauter pour déterminer le périmètre. 
|
« Comment la corde à sauter vous aide-t-elle à déterminer le périmètre de votre gâteau? » « Que pourriez-vous utiliser pour obtenir une mesure plus exacte? » (Nous pourrions mesurer la forme créée à l'aide d'unités de mesure conventionnelles.) |
Amorcer une discussion pour aider les élèves à comprendre la façon dont elles et ils peuvent déterminer le gâteau qui a le plus grand périmètre. Faire réaliser aux élèves que pour comparer les périmètres des gâteaux, elles et ils doivent utiliser la même unité de mesure (par exemple, centimètre [cm]). Demander aux élèves de déterminer le périmètre de leur gâteau en centimètres.
Comparer les résultats obtenus lors d’un échange mathématique et déterminer le gâteau qui a le plus grand périmètre.
Prolongement – 1
Discuter avec les élèves d’un autre attribut du gâteau qu’il est possible de mesurer. Poser des questions telles que :
- Quel autre attribut de votre gâteau est-il possible de déterminer? (Il est possible de déterminer l’aire de la surface de notre gâteau.)
- Quels objets étalons peut-on utiliser pour déterminer l’aire de la surface de votre gâteau? (On pourrait utiliser des papillons adhésifs.)
- Que doit-on faire pour être capable de comparer les aires des surfaces des gâteaux? (On peut comparer les pièces utilisées ou on peut compter le nombre de papillons adhésifs utilisés pour recouvrir la surface.)
- Les aires des surfaces des gâteaux seront-elles semblables ou différentes? Justifiez votre réponse. (Si les équipes ont utilisé les mêmes pièces, les aires des surfaces des gâteaux seront égales. Par contre, si les équipes n’ont pas utilisé les mêmes pièces, les aires des surfaces des gâteaux seront différentes.)
Allouer du temps aux équipes pour déterminer l’aire de leur gâteau et comparer les résultats obtenus lors d’un échange mathématique.
Prolongement – 2
Remettre à chaque élève un ensemble de tangram et lui demander de construire un gâteau avec le plus petit ou le plus grand périmètre possible ou dont la surface a la plus petite ou la plus grande aire possible en utilisant toutes les pièces du tangram.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison, les élèves peuvent :
- déterminer la pièce qui a le plus petit ou le plus grand périmètre.
- déterminer la fenêtre qui a le plus grand ou le plus petit périmètre.
- déterminer le périmètre et l’aire de la surface d’une nappe en utilisant des mesures non conventionnelles (par exemple, avec des napperons).
- déterminer un objet (par exemple, une nappe, un couvre-lit) qui a le plus grand périmètre ou a la surface ayant la plus grande aire.
- trouver l’aire de moules à gâteaux à l’aide d’unités non conventionnelles et conventionnelles.
Les tracer sur une feuille de papier quadrillé, noter les mesures dans un tableau et les ordonner en ordre croissant par exemple.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 153-165.
