E1.3 Décrire et effectuer des translations et des réflexions dans une grille, et prédire les résultats de ces transformations.
HABILETÉ : DÉCRIRE ET EFFECTUER DES TRANSLATIONS DANS UNE GRILLE
En 4e année, les élèves décrivent et effectuent des translations verticale, horizontale et oblique. Par exemple, pour décrire et effectuer une translation oblique, il faut vérifier à la fois le déplacement horizontal et le déplacement vertical. Pour ce faire, les élèves utilisent une notation symbolique entre parenthèses. Par exemple, une translation de trois unités vers la droite et de deux unités vers le bas est représentée symboliquement par (3 D, 2 B) ou (3 →, 2 ↓). Il est préférable d’habituer les élèves à toujours décrire la translation en indiquant d’abord le déplacement horizontal et ensuite le déplacement vertical.
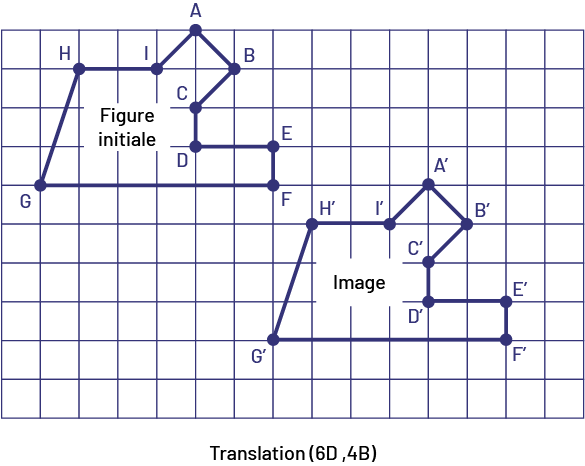image Une
grille de neuf colonnes et 15 rangées. Il y a deux figures placées obliquement sur la grille. Dans la première est
écrit figure initiale; dans la seconde est écrit image. Les points « a », « b », « c », « d », « e », « f », « g », «
h », et « i » sont identifiés sur la figure initiale. Les points « a » apostrophe, « b » apostrophe, « c » apostrophe,
« d » apostrophe, « e », « f » apostrophe, « g » apostrophe, « h » apostrophe, et « i » apostrophe sont identifiés sur
la figure initiale.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 28-29.
HABILETÉ : DÉCRIRE ET EFFECTUER DES RÉFLEXIONS DANS UNE GRILLE
Pour décrire et effectuer une réflexion, il faut comprendre que tous les points sur la figure initiale et les points correspondants sur l’image sont à égale distance de l’axe de réflexion. La réflexion entraîne un changement de la position et de l’orientation originales de la forme, mais l’image réfléchie est congruente à la forme originale. En d’autres mots, l’image réfléchie a la même taille et la même forme, mais elle sera « orientée » dans une autre direction, et se trouvera dans une autre position. Il est important de noter que l’axe de réflexion peut être tracé dans n’importe quelle direction par rapport à la forme originale – horizontalement, verticalement ou diagonalement – selon n’importe quel angle. Toutefois, les réflexions à partir d’un axe de réflexion diagonal seront abordées en 5e année.
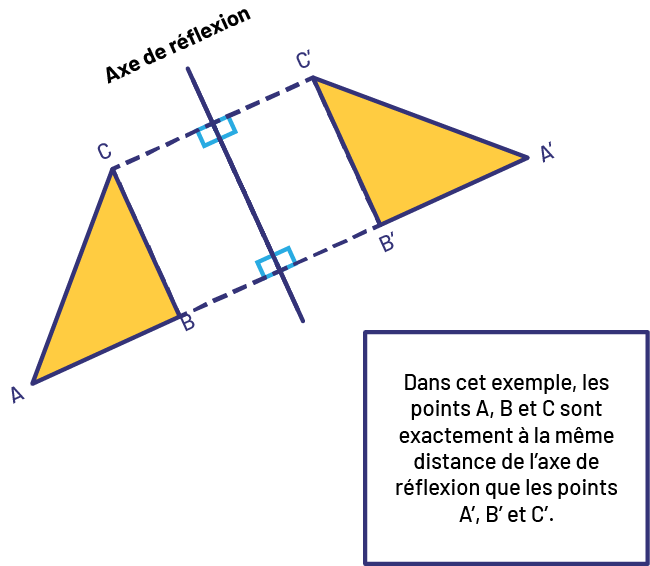image Un quadrilatère formé d’un rectangle et de deux triangles
congrus, de côté opposé. Un trait passe à travers le centre de la figure. D’un côté, les points « a », « b », et « c »
sont identifiés; de l’autre côté, les points « a » apostrophe, « b » apostrophe, et « c » apostrophe sont identifiés.
Source: A Guide to effective Instruction in Mathematics, Kidergarten to Grade 6, p. 35.
Les élèves effectuent des réflexions de figures simples et complexes sur du papier à points et du papier quadrillé, à l’aide du Mira et de papier calque ou d’un logiciel de géométrie.
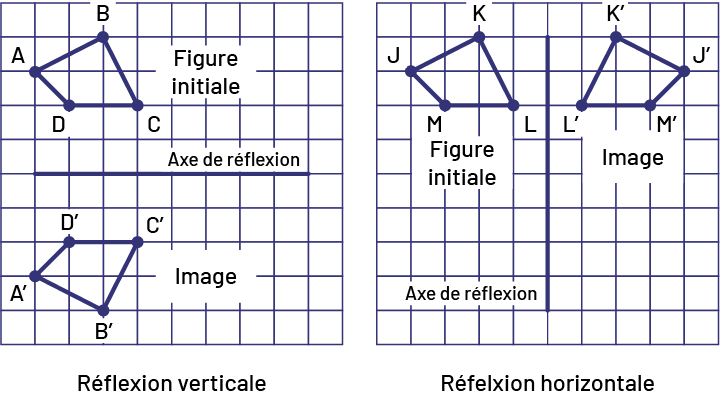image
Il y a deux grilles: la première représente une réflexion verticale, et la deuxième représente une réflexion
horizontale. Dans la première grille, deux quadrilatères congrus sont d’un côté chacun d’une ligne horizontale, nommée
l’axe de réflexion. Le premier quadrilatère est la figure initiale; le deuxième quadrilatère est l’image. Dans la
deuxième grille, deux quadrilatères congrus sont d’un côté chacun, d’une ligne verticale, nommés l’axe de réflexion.
Le premier quadrilatère est la figure initiale; le deuxième quadrilatère est l’image.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31.
HABILETÉ : PRÉDIRE LES RÉSULTATS DES TRANSLATIONS ET DES RÉFLEXIONS
Au cours du cycle moyen, les élèves prédisent le résultat d’une transformation et décrivent ce qui arrivera à l’objet lorsque la transformation sera effectuée. Grâce à des recherches guidées, les élèves seront finalement capables d’observer l’orientation initiale d’un objet et le résultat d’une transformation, et de décrire la transformation effectuée sans devoir la voir.
Source: A Guide to effective Instruction in Mathematics, Kidergarten to Grade 6, p. 34.
CONNAISSANCE : TRANSLATION
Une translation peut être décrite comme une transformation qui fait glisser chaque point d’une forme à la même
distance et dans la même direction. Pendant une translation, l’orientation de la forme ne change pas et l’image est
congruente à la forme originale. Une translation peut se produire dans n’importe quelle direction.
Source: A Guide to effective Instruction in Mathematics, Kidergarten to Grade 6, p. 35.
CONNAISSANCE : RÉFLEXION
Une réflexion est une transformation dans laquelle tous les points sur la figure initiale et les points correspondants sur l’image sont à égale distance de l’axe de réflexion.
Source: A Guide to effective Instruction in Mathematics, Kidergarten to Grade 6, p. 35.